Приемы учебной работы при обучении решению задач на доказательство. Как научить ребенка решать задачи по геометрии 7 класс
Приемы учебной работы при обучении решению задач на доказательство
Разделы: Математика
Обучение доказательствам – одна из важнейших
целей обучения математике.
Именно при выполнении доказательств
оттачивается логическое мышление учеников,
разрабатываются логические схемы решения задач,
возникает потребность учащихся в обосновании
математических фактов.
Начиная изучать геометрию, учащиеся способны
осознать необходимость доказательства, однако
осуществлению доказательства им только
предстоит научиться.
С задачами на доказательство учащиеся
встречаются при изучении второй темы курса
геометрии 7-го класса “Треугольники”. Опыт
проведения доказательств отсутствует. Учащиеся
не владеют геометрическим языком, многие не
понимают смысла слова “доказать”, поэтому
испытывают большие трудности. Я решаю эту
проблему, предоставляя учащимся образцы
(алгоритмы) доказательства. В ходе изучения
теоретического материала вместе с учениками
составляем алгоритмы решения задач каждого вида
и красочно оформляем их в виде книжки.
Эта книга помогает учащимся в затруднительных
случаях быстро найти сходную задачу, вспомнить
алгоритм решения, составить план решения.
СМ ПРИЛОЖЕНИЕ
1
Обучение решению задач веду постепенно.
7-й класс
Тема “Треугольники”
- Алгоритм решения задачи: доказать, что
треугольник … равен треугольнику….
- Алгоритм решения задачи: доказать, что отрезок…
равен отрезку….
- Алгоритм решения задачи: доказать, что угол …
равен углу ….
- Алгоритм решения задачи: доказать, что отрезок
… является биссектрисой.
- Алгоритм решения задачи: доказать, что отрезок
… является медианой.
- Алгоритм решения задачи: доказать, что отрезок
… является высотой.
- Алгоритм решение задачи: доказать, что
треугольник … равнобедренный.
Тема “Параллельные прямые”
1.Алгоритм решение задачи: доказать, что прямая
… параллельна прямой ….
Тема “Прямоугольный треугольник”
1.Алгоритм решение задачи: доказать, что
прямоугольные треугольники … равны
8-й класс
Тема “Параллелограмм”.
1.Алгоритм решение задачи: доказать, что
четырехугольник…. будет параллелограммом.
Тема “Подобие треугольников”.
1.Алгоритм решение задачи: доказать, что
треугольник …. подобен треугольнику…
Принцип пошаговости формирует навыки решения
задач и навыки построения логических цепочек
доказательства.
Решение задач учу начинать с предложения
“Чтобы доказать, что …”. Ученик называет то, что
требуется доказать в конкретной задаче и ведет
доказательство по соответствующему алгоритму.
Такой ход решения позволяет учащимся понимать
смысл поставленной задачи, выстраивать
аргументацию, формирует умение анализировать,
развивает логическое мышление.
Работая в дальнейшем по модели, ученик на
каждом шагу контролирует свои действия,
обращаясь к выведенному алгоритму. На любом
этапе работы ученик может по сигналу учителя
передать “эстафету” решения любому ученику.
Этим достигается предельное внимание при
решении задачи.
Красочно оформленные алгоритмы учащиеся
запоминают быстро. И к концу изучения темы
“Признаки равенства треугольников” многие
учащиеся хорошо проводят доказательные
рассуждения, точно и грамотно выражают свои
мысли. Данные алгоритмы учащиеся применяют и при
доказательстве теорем.
Разработанные алгоритмы позволили
логически упорядочить материал, дать его
компактное и наглядное изложение. Они
способствуют как подсознательному запоминанию,
так и осознанному усвоению материала. При
пользовании алгоритмами учащиеся лучше
осмысливают, осознают логические взаимосвязи.
Это помогает им научиться решать задачи.
Пример решения задачи учениками 7-го
класса по теме
“Признаки равенства
треугольников”
Дано АВ=ВС, АD =DC
Доказать BD – биссектриса ABC
Ответ ученика
(Устно). Чтобы доказать, что BD биссектриса, нужно
доказать, что угол ABD равен углу DBC.Чтобы доказать,
что два угла равны, нужно доказать, что равны
треугольники, содержащие эти углы
Работа в тетради. Рассмотрим ABD и BDC
(Устно) Чтобы доказать, что два треугольника
равны, найдем у них три равных элемента.
Работа в тетради
АВ = ВС по условию задачи,
АD = DC по условию задачи,
BD – общая.
Значит ABD = BDC по третьему
признаку равенства треугольников.
В равных треугольниках соответственные
элементы равны.
Значит, угол ABD равен углу DBC.
Следовательно, BD-биссектриса по определению
биссектрисы угла.
Алгоритмы решения задач на
доказательство.
Задача на доказательство – это утверждение,
которое необходимо доказать с помощью аксиом и
теорем.
Алгоритм решения задачи: доказать,
что треугольник… равен треугольнику … .
Доказательство ведется на основе признаков
равенства треугольников.
1 признак
Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам
и углу между ними другого треугольника, то такие
треугольники равны
2 признак
Если сторона и два прилежащих к ней угла одного
треугольника соответственно равны стороне и
двум прилежащим к ней углам другого
треугольника, то такие треугольники равны
3 признак
Если три стороны одного треугольника
соответственно равны трем сторонам другого
треугольника, то такие треугольники равны
Алгоритм решения задачи: доказать, что
отрезок … равен отрезку ….
В равных треугольниках соответственные
элементы равны.
Поэтому
Продолжение статьи
Приложение
Рисунки
xn--i1abbnckbmcl9fb.xn--p1ai
Как научить решать ребенка задачи по геометрии?

Огромное количество учеников имеет трудности в решении задач по геометрии. Это усугубляется тем, что многие оценки по данной дисциплине в школах ставятся учащимся за знание теорем, в то время как практической части уделяется недостаточное количество времени: учитель успевает объяснить за урок у доски всего два–три примера.
Советы репетиторам:
1. Помните, что геометрия содержит в себе фиксированный набор тем, изучаемых строго в хронологическом порядке. Почти всегда незнания ученика представляют собой «снежный ком», и сложности при решении задачи возникают из-за не усвоенных знаний по предыдущим темам. Необходимо найти тот самый момент, с которого ученик перестал понимать предмет, и начать объяснение именно с него.
2. Любая теория должна подкрепляться практикой. Как только вы объяснили тему, сразу дайте ребенку несколько задач, добейтесь того, чтобы он решал их самостоятельно без вашей подсказки.
3. Максимально упростите решаемые примеры: в идеале ответ должен находиться в одно действие, - это натолкнет ученика на мысль о том, что геометрия не такой сложный предмет, как ему казалось раньше. Постепенно давайте задачи посложнее.
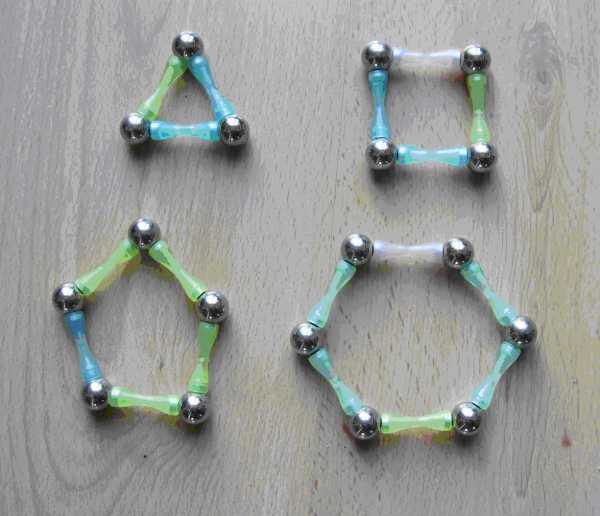
4. Формулируйте задачи в виде рисунков, а не текста. Старайтесь развивать у ребенка воображение, при объяснении пользуйтесь вспомогательным материалом, например, детским конструктором.
5. Всегда спрашивайте, какую теорему или свойство он применяет на каждом шаге решения. Необходимо, чтобы усилия вашего подопечного превратились не в обычную зубрежку, а в понимание, как теория используется на практике.
6. Систематически давайте ребенку однотипные задачи по пройденным темам раз в две недели на протяжении нескольких месяцев, теорию спрашивайте устно. Чтобы самому не забыть, сколько раз и когда вы повторили с учеником изученный материал, ведите календарь, в котором будете это фиксировать.
7. Уделяйте внимание теории. Прежде чем заставлять ребенка выучить точную формулировку теоремы, просите объяснить ее своими словами: важно добиться понимания нового материала.
Что делать, когда у ребенка есть большие пробелы в знаниях?
Часто случается так, что ученик очень сильно запускает предмет. Тогда перед вами встает вопрос о том, объяснять ли предмет с самого начала или продолжать «разжевывать» каждую задачу по отдельности. Обязательно посоветуйтесь с родителями ребенка, объясните, что в случае выбора первого варианта промежуточные оценки в школе, скорее всего, не улучшатся, и на это уйдет гораздо больше времени, но в перспективе выбранный подход даст лучшие результаты.
Автор: Пономарев Михаил Александрович
http://www.spb.upstudy.ru/repetitors/196613/
Поделиться в соц. сетях -
upstudy.ru
Геометрия с нуля
Разделы: Математика
В 21 веке, несмотря на активное развитие науки, у многих школьников Российской Федерации такая наука, как геометрия вызывает все больше затруднений, а какая-то часть детей и вовсе не может решать простейшие геометрические задачи. Поэтому необходимо признать тот факт, что восприятие у нового поколения совершенно иное, и дело тут вовсе не в их деградации. Дети все также хотят развиваться: читают книги, смотрят научные фильмы и проводят эксперименты. Но самое главное, чего они не хотят, так это заучивать то, чего не понимают. На основе этого утверждения как раз и будет построена моя программа.
Представим, что перед нами сидит человек, который вообще не представляет, что такое геометрия. А именно так и выглядит бОльшая часть детей приходящих в 7 класс. Этот человек не в состоянии накладывать треугольники друг на друга и тем более не может делать из этого какие-то выводы. Поэтому сначала его нужно долго и упорно знакомить его с геометрией, чтобы в итоге он понял, насколько она проста и полюбил ее.
Разделение на уровни
Прежде всего, необходимо понять, что должен знать ребенок на определенном этапе. Для этого нужно разделить геометрию (планиметрию 7-9 класса) на 3 уровня:
- Базовый уровень: школьник знает(не обязательно наизусть) и понимает простейшие теоремы, а также решает незамысловатые задачи;
- Средний уровень: школьник умеет доказывать теоремы и решать задачи, используя доказательства;
- Высокий уровень: школьник знает сложные теоремы и умеет решать сложные задачи.
Именно эти три пункта будут подробно описаны в статье.
Базовый уровень (простейшая теория и задачи)
- понятие точки, прямой, луча, отрезка, угла, фигуры и т.д.
Прежде всего, школьник должен понять, с чем он будет иметь дело на протяжении ближайших трех лет, поэтому начинать необходимо с вводного курса. Не надо давать детям сложные задачи, а их надо просто познакомить с геометрией.
- углы (по градусам)
Углам нужно уделить особое внимание, потому что далеко не все дети могут в пространстве могут отличить тупой угол от прямого. Кроме того, максимум внимания нужно уделить развернутому углу, потому что на нем будет основан следующий пункт.
- смежные углы
Многим детям тяжело запомнить существующее определение смежных углов, и именно в большинстве случаев начинаются первые проблемы с геометрией. Поэтому мною будет предложено новое определение смежных углов: “Смежные углы – это углы, полученные в результате деления развернутого угла на две части.” Если уделить должное время развернутому углу, то получится сэкономить время на объяснении свойства смежных углов, т.к. оно итак будет понятно.
- вертикальные углы
Вертикальные углы, также как и смежные, имеют весьма непростое определение, которое можно заменить ан более просто. Достаточно ограничиться следующим: “Вертикальные углы-это углы между пересекающимися прямыми.”, а далее просто постараться разобрать как можно больше примеров, связанных с вертикальными и смежными углами.
- перпендикулярные прямые
Этой теме я не стану уделять много внимания, т.к. он итак понятен большинству школьников.
- параллельные прямые
Вместо равенства треугольников гораздо лучше рассматривать параллельные прямые, т.к., помимо получения новой информации, дети закрепляют старую, используя вертикальные и смежные углы при решении задач на параллельные прямые. Объяснять данную тему проще с признака, основанного на внутренних односторонних углах, т.к. единственное, что запоминают дети после шестого класса, это что сумма углов треугольника равна 180 градусам. Опираясь на это можно представить, что прямые пересекутся и образуют с секущей треугольник, сумма углов которого равна 180 градусам. А после этого показать детям вариант, при котором треугольника не будет, т.е. когда внутренние односторонние углы заберут градусную меру третьего угла треугольника. После этого остальные признаки доказать уже будет не так и сложно. Самое главное, не надо заставлять детей учить первые доказательства, т.к. они должны их понять.
- биссектриса, высота и медиана
После всех предыдущих тем, ребенок будет понимать, что такое углы и уметь с ними работать, а также будет знаком с прямыми, отрезками, фигурами и прочим. В этот момент ему уже можно давать более-менее сложные темы, которые ему в дальнейшем будут постоянно пригождаться. В определениях ничего менять не стоит, т.к. они итак максимально доступны. Единственное, что нужно обязательно сделать, так это убедиться в том, что ребенок может провести биссектрисы, медианы и высоты в любой фигуре и из любой вершины!
- треугольники *(при объяснении свойств треугольников можно и нужно опираться на признаки равенства)
Теперь, когда школьник со знаком с основами, можно приступать к рассмотрению фигур. Начать лучше всего с треугольников, т.к. именно они используются в большинстве задач. Здесь необходимо рассмотреть все виды треугольников с их свойствами. Объяснить ребенку откуда что берется, опять же не заставляя это заучивать. Но определения и свойства школьник должен знать, т.к. именно на этапе прохождения свойств фигур, мы можем начинать спрашивать с ребенка теорию. Теперь он уже полноценно вовлечен в процесс.
- четырехугольники *(при объяснении свойств четырехугольников можно и нужно опираться на признаки равенства)
Здесь я бы хотела представить Вашему вниманию увлекательный процесс эволюции параллелограмма, который детям запомнить гораздо проще, чем определения из учебника:
Здесь рассмотрены только те свойства, которые способен легко усвоить школьник на базовом уровне.
Кроме того, сюда же необходимо включить и трапецию со всеми ее свойствами и разновидностями.
Таким образом, мы сможем закрепить параллельные прямые и понять, откуда что берется в четырехугольниках.
- многоугольники
В этой теме необходимо рассмотреть разные виды многоугольников и сумму углов n-угольника.
- теорема Пифагора
Тема, которую итак все прекрасно понимают, поэтому ничего усложнять не надо.
- площади
Здесь я опять же хочу предложить удобную схему, которую необходимо объяснять с помощью бумажных фигурок.
Трапеция опять же рассматривается отдельно.
- подобие и первый признак подобия
Рассматривается исключительно в ознакомительных целях, чтобы детям легче было понимать начала тригонометрии.
- средние линии треугольника и трапеции
Средние линии лучше рассматривать вместе, потому что так они лучше усваиваются.
- тригонометрия
В самом начала тригонометрии, школьникам стоит напомнить о том, что такое соотношения, а после очень много времени посвятить самим определениям синуса, косинуса, тангенса и котангенса, чтобы школьники понимали, откуда взялись эти странные английские буквы. Затем необходимо рассмотреть множество задач, в которых они будут использоваться. Удобнее всего давать задачи на теорему Пифагора и площади. Желательно уже на базовом уровне ознакомить детей с таблицей, т.к. сейчас они уже максимально близки к среднему и уровню и способны усваивать информацию средней сложности.
- окружность и круг
И, наконец, последняя тема на базовом уровне. Здесь необходимо напоминать детям обо всем, что связано с окружностью и кругом, начиная с определений, т.к. никто уже ничего не помнит из курса 6 класса. А также стоит рассмотреть свойство касательной, вписанный и центральный углы, и свойство гипотенузы прямоугольного треугольника.
На этом базовый курс окончен. У рядового школьника достаточно базовых знаний, на которые он мог бы опираться при решении задач, с использованием доказательств. Пришла пора поближе с ними познакомиться.
Средний уровень (доказательства)
Расписывать программу для среднего уровня смысла нет, т.к. на этом этапе ребенок готов усваивать практически любую информацию и способен аргументированно решать задачи на доказательства. Единственное, что стоит сделать, так это перечислить темы среднего уровня:
- соотношения между сторонами и углами;
- неравенство треугольника;
- признаки равенства треугольников;
- признаки подобия треугольников;
- четыре замечательные точки;
- вписанная и описанная окружности.
Этого вполне достаточно для доказательств средней степени сложности.
Высокий уровень (сложные доказательства и решение сложных задач)
К сожалению, немногие могут достичь высокого уровня, но каждый должен хотя бы попытаться. Опять же, нет смысла все подробно расписывать, поэтому будут перечислены лишь темы:
- теорема Фалеса;
- теорема Герона;
- теорема синусов;
- теорема косинусов;
- углы при окружности;
- хорды окружности;
- и т.д.
Заключение
Из всего вышесказанного можно сделать следующий вывод: прогресс любого школьника основан на его базовых знаниях. Если они есть, то их необходимо лишь грамотно развивать. Поэтому, прежде всего, необходимо упростить получение базовых знаний и сделать их максимально доступными для всех школьников без исключения.
Примечание: векторы в статье не учтены, т.к. являются дополнением ко всему вышесказанному.
xn--i1abbnckbmcl9fb.xn--p1ai
Как решать задачи по геометрии: практические советы и рекомендации
Как решать задачи по геометрии? Многие учащиеся задаются этим вопросом на протяжении многих лет. Иногда даже сам предмет вызывает страх и отвращение из-за непонимания отдельных тем. Потом бывает очень сложно преодолеть неприязнь к геометрии и снова с заинтересованностью посещать уроки.
В чем причина
Во многом все зависит от того, как преподаватель объясняет свой предмет. Если учитель сможет заинтересовать учеников, дальше дело пойдет по накатанной, и каждый урок будет захватывающим. Дети даже будут оставаться на переменке, чтобы успеть решить как можно больше задач.
Если вам плохо объясняли этот предмет или есть еще какие-то причины, по которым у вас совершенно не получается вникнуть в тему, эта статья поможет разобраться.

Как научиться решать задачи по геометрии?
Для начала нужно понять, что за один день вы вряд ли далеко продвинетесь в своих знаниях, так что настраивайтесь на длительный процесс обучения.
Также нужно определиться с целью. Если вам нужно просто решить задачу по геометрии, чтобы не получить плохую оценку за контрольную работу, достаточно лишь выучить определенную тему и потренироваться в практических аспектах.
Что делать?
Возьмите учебник и пролистайте последние несколько параграфов, которые вы изучили. Постарайтесь вникнуть в информацию, поймите, что от этого зависит то, как будут оценены ваши знания. Теперь можете взять листочек и изучить несколько задач, обязательно смотрите в текст учебника и пытайтесь понять алгоритм решения.
Если что-то не получается, обратитесь к решебнику, который выпущен специально под ваш учебник. Только не списывайте абсолютно все, старайтесь понять, как решать задачи по геометрии.
Вспомните, о чем говорил преподаватель на занятиях, возможно, какая-то информация окажется полезной.
Не стоит пренебрегать и человеческим фактором. Хорошо знающие предмет школьники или студенты не откажут вам в помощи. Некоторые из них могут объяснить гораздо доходчивее преподавателей.
А тем, кто решил не просто разобраться в отдельных темах, а научиться решать задачи и как орешки их щелкать, нужно основательно потрудиться.

Во-первых, главное – это мотивировать себя на дальнейшие занятия. Бывает так, что вопрос о том, как научиться решать задачи по геометрии, встает лишь один раз, а потом начинается просто списывание примеров из интернета. Так делать крайне нежелательно.
Развивайте усидчивость. Посмотреть в решебник намного проще, разумеется, но подумайте, какое наслаждение вы испытаете, когда самостоятельно решите сложную задачку. Поэтому лучше лишние полчаса посидеть за учебником, чем стараться списать побыстрее чье-то решение.
Может быть, геометрия вам понадобится для будущей профессии. Тогда тем более не стоит откладывать дело в долгий ящик, нужно приниматься за задачи прямо сейчас.

Во-вторых, практика, и только она, поможет вам стать на шаг ближе к своей цели!
Заведите привычку узнавать что-то новое каждый день. Просто старайтесь с утра решать одну задачу, а потом проверяйте по ключам ее правильность. Позже заметите, что с каждым днем процесс идет все быстрее и качественнее.
Самое главное здесь – не сдаваться и не обращать внимания на мелкие трудности. Если вы включите в распорядок дня этот совет, то вопрос о том, как решать задачи по геометрии, отпадет сам собой.
В-третьих, обращайтесь за помощью к знакомым.
Не бойтесь в школе лишний раз поднять руку и выйти к доске, чтобы решить сложный пример, который никто не отважился постичь. Даже если что-то пойдет не так, и вам не удастся сделать задание, ничего страшного в этом нет. Преподаватель объяснит решение примера и даже похвалит вас за смелость. Также это неплохой способ показать свои знания одноклассникам.
Ребята могут помочь с выполнением заданий, когда узнают, что вы настроены серьезно в изучении предмета.

Не вешаем нос!
Не отчаивайтесь, если никто не откликнулся на вашу просьбу. Всегда можно обратиться за помощью к репетитору, который точно объяснит, как решить задачу по геометрии. Даже при ограничении в денежных средствах хорошим выходом станут занятия по скайпу, которые ничем не хуже уроков, проходящих при личной встрече.
Вот и все советы. Будем надеяться, что вы все-таки поняли, как решать задачи по геометрии. В любом случае старайтесь применять эти методы на практике, и вы осуществите задуманное!
fb.ru
Как научить решать ребенка задачи по геометрии
Documents войти Загрузить × - Иностранные языки
advertisement advertisement Related documents
Подготовила: ученица 7 «Б» класса Котельникова София Проверил:

Если ребенок часто обманывает

Тематика дипломных и курсовых работ

Рекомендации по работе с тревожными детьми Хвалите

как научить ребенка понимать алгебру

Рекомендации_презентация_Задачи на построение(геометрия
Геометрия и космичесвие объекты

Приложение 1.
Наука 27 сентября 2013 года.

Обыкновенные дифференциальные уравнения

Если ребенок часто обманывает
Первый урок геометрии.

Феномен Апокалипсиса от древности до наших дней

дом задание на каникулы
studydoc.ru
У меня часто спрашивают: "Как понять геометрию 7 класса?" | Геометрия
У меня часто спрашивают: «Как понять геометрию 7 класса?» Из своего опыта могу сказать, что любое дело требует от каждого из нас в первую очередь изучения теории. И только потом, понимая, о чём идёт речь, можно приступать к практике. Так же и с геометрией. В первую очередь необходимо понять и изучить её определения, теоремы, а затем начинать регулярные, именно регулярные действия по решению задач. Например, если не понять на рисунках или чертежах, а затем не выучить определения смежных и вертикальных углов, то вряд ли можно будет решить хоть одну задачу с ними. А ведь определение совсем простое: если нам даны две пересекающиеся прямые, то они образуют четыре угла. Те углы, которые имеют общую сторону, называются смежными, а те, которые не имеют общих сторон — вертикальные. На данном рисунке углы a и b, a и c, c и d, d и b — смежные. А углы a и d, c и b — вертикальные. Смежные углы в сумме составляют 180 градусов, а вертикальные углы равны между собой. Теперь, зная только эти определения и видя рисунок, мы можем начать решать задачи на смежные и вертикальные углы.
Задача 1. На прямой АВ взята точка С и из неё проведён луч СD таким образом, что угол ACD в 4 раза больше, чем угол BCD. Определить величину этих углов. Решение: Пусть угол BCD будет Х, тогда угол ACD будет 4Х. В сумме эти углы составляют 180 градусов. Значит, имеем уравнение: Х+4Х = 180 5Х=180 Х= 36. 4Х= 36*4 = 144. Ответ: угол BCD = 36 градусов. Угол ACD = 144 градуса.
Задача 2. Определить 2 смежных угла, один из которых на 20 градусов больше другого. Решение: Пусть один угол равен Х, тогда другой равен Х+20. Составляем уравнение Х+Х+20 = 180 2Х+20 = 180 2Х=180 — 20 2Х=160 Х=160/2 Х=80. Первый угол равен 80 градусов, тогда второй — 80 + 20 = 100 градусов.
Задача 3. Даны две пересекающиеся прямые. 2 угла, образованных этими прямыми относятся как 2:6. Найти остальные углы. Решение: Если два угла относятся как 2:6, то это смежные углы. Ведь углы вертикальные равны и относятся друг к другу как 1:1. Итак, первый угол равен 2Х, второй 6Х. В сумме они дают 180 градусов. Имеем: 2Х+6Х=180 8Х=180 Х=180/8 = 22,5 градуса. Первый угол равен 22,5*2 = 45 градусов, второй 22,5*6 = 135 градусов, третий = 45 градусов, четвёртый = 135 градусов.
Задача 4. Один из четырех углов, который образован при пересечении двух прямых, равен 54 градуса. Определить остальные углы. Решение: Ещё один угол, как вертикальный будет равен 54 градуса. Смежные углы с углом в 54 градуса будут равны 180-54 = 126 градуса. Ответ: 1-й угол 54, 2-й угол 54, 3-й угол 126, 4-й угол 126.
Задача 5. 2 прямые пересекаются в точке О. Сумма двух углов равна 220 градусов. Определить все углы. Решение: Если сумма углов равна 220 градусов, то это углы вертикальные, ведь если бы они были смежными, тогда их сумма была бы равна 180 градусов. А если это углы вертикальные, то они равны. Значит, каждый из них равен 220:2 = 110 градусов. Смежные с ними углы равны 180-110 = 70 градусов. Ответ: 110, 110, 70, 70. Задача 6. Данный угол и смежные с ним составляют в сумме 293 градуса. Найти все углы. Решение: Если три угла в сумме равны 293 градуса, то, поскольку все четыре угла в сумме равны 360 градусов, четвёртый угол будет равен 360-293 = 67 градусов. Смежные с ним будут равны 180-67 = 113 градусов. А первый, как вертикальный, равен четвёртому и равен 67 градусов. Ответ: 113, 113, 67, 67. В следующий раз мы продолжим отвечать на вопрос: «Как понять геометрию 7 класса».
Вам так же будет интересно:
Оставить комментарий
geometriyaprosto.ru
Как помочь ребенку освоить геометрию? – Citywoman
Геометрия очень важна для развития мыслительных способностей ребенка, она способствует полноценному осознанию окружающего мира. Этот раздел математики достаточно сложен для восприятия школьниками, потому что оперирует строгими утверждениями и закономерностями. Учебники, к сожалению, не всегда способны представить все в доступной и понятной для детей форме, поэтому ребенку необходима помощь в успешном изучении геометрии.
Геометрия и другие дисциплины
Помочь ребенку в изучении геометрии можно гораздо раньше, чем этот предмет появится в его школьной программе. Для понимания этой области науки необходимо развивать пространственное воображение, в этом поможет география, рисование, природоведение, труд, лепка, оригами, конструкторы. Обучение можно превратить в интересную и захватывающую игру, чтобы ребенок получал знания с удовольствием!
Что делать, если ребенок запустил учебу
Учиться нужно систематически, нельзя пропускать материал, который с первого раза кажется непонятным. Но если пробелы в обучении накопились, и геометрия совершенно не поддается школьнику, не стоит опускать руки — все поправимо!
- Поговорите с ребенком, нужно разобраться в причинах плохой учебы. Не надо ругаться и давить на школьника, постарайтесь понять, что мешает ему в изучении геометрии. Возможно, у ребенка сложности с педагогом.
- Если школьник утверждает, что предмет ему непонятен, узнайте, на каком этапе он это осознал. Стоит вернуться к тому разделу геометрии, который был слишком сложным для ребенка и начать изучать его заново, постепенно переходя к другим темам. Повторяйте пройденный материал вновь и вновь, пока в этом будет необходимость.
- Начните заниматься с ребенком самостоятельно, повторите азы. Убедитесь, что ему понятны основные определения и термины, он правильно оценивает характеристики тел и фигур — это основа, без которой невозможно успешное изучение предмета.
- Умение строить чертежи необходимо, именно они позволяют визуально представить условия любой задачи, увидеть фигуры наглядно. Приучите ребенка к обязательному использованию чертежей, они облегчат учебу.
- Используйте аналогии. Детям иногда сложно разбираться в абстрактных взаимосвязях, поэтому можно экспериментировать — определяя гипотенузу треугольника, например, можно представить, что вы высчитываете точное расстояние от дома до дачи.
- Уделяйте большое внимание практическим задачам, потому что простое заучивание теории — это бесполезное занятие, для хорошего понимания предмета этого катастрофически мало. Да, ребенку должна быть хорошо знакома аксиома параллельных прямых и основные определения, но ему также надо уметь доказывать теоремы и применять теоретические знания на практике.
Если ребенок ошибается, не ругайте его, а позвольте ему найти и исправить свои ошибки самостоятельно, при необходимости помогите и объясните непонятные моменты. Школьник должен научиться понимать, что и почему он делает неверно, это поможет быть более внимательным в будущем.
Профессиональная помощь
Помочь ребенку в освоении геометрии может репетитор. Безусловно, придется потратить время на поиск хорошего учителя и деньги, но в результате ребенок сможет лучше узнать геометрию и даже выйти за рамки школьной программы, избавиться от трудностей, которые мешают полноценно учиться в школе.
Если нет возможности нанимать репетитора, есть достойная альтернатива — видеоуроки, например, на сайте http://interneturok.ru/, благодаря которым школьник сможет получить все те знания, которых ему не хватает. Видеоуроки, пожалуй, даже удобнее — заниматься можно в любое удобное время, при необходимости видео можно остановить или просмотреть заново. Ищите и используйте возможности для помощи ребенку в обучении!
www.citywoman.info