Урок в 6 классе «Основные методы решения линейных уравнений». Как научить ребенка решать уравнения за 6 класс
как решать уравнения 6 класс
При решении уравнений необходимо помнить и в при необходимости использовать следующие правила:
- Можно умножить или разделить обе части уравнения на одно и то же число, которое не равно нулю, при этом корни данного уравнения останутся неизменными.
Например:
Найдем корни данного уравнения:
Попробуем умножить левую и правую часть уравнения на число 9:
Теперь найдем корни полученного уравнения:
- При решении уравнения его слагаемые можно перенести из одной части уравнения в другую, при этом изменяя их знак на противоположный. В таком случае корни уравнения не меняются.
Например:Рассмотрим уравнение .Чтобы его решить, перенесем число —13 в правую часть уравнения, изменяя его знак на противоположный (на +):
Проверим правильность найденного корня, подставив его значение в исходное уравнение:
Корень найден правильно.
- Если в уравнении есть подобные слагаемые, то нужно все слагаемые с переменной перенести в одну часть уравнения (обычно в левую), а постоянные — в другую часть уравнения (в правую).}
Например:
ru.solverbook.com
О методике работы репетитора по математике с темой «решение уравнений» в 5-6 классах
Знакомство ребенка с уравнениями начинается почти с самого начала изучения математики, задолго до ЕГЭ и, как правило, задолго до обращения к репетитору. Еще в младшей школе решаются простейшие алгебраические уравнения, которые служат фундаментом для построения алгоритмов решения уравнений в 11 классе. Каких только разновидностей уравнений не встретишь в школе: алгебраические, иррациональные, тригонометрические, показательные, логарифмические. Голова идет кругом. При этом, почти к каждому разделу учебника математики прикрепляются уравнения определенного вида с различной комбинацией изученных действий, функций и разным уровнем сложности. Репетитору по математике важно помнить о том, что методы обучения решению уравнений на разных этапах освоения предмета имеют много общего, так как по сути перед учеником ставится одна и та же задача — подбор числа или чисел, удовлетворяющих данному равенству.
Основы работы с уравнениями закладываются задолго до 11 класса и объясняются на простых математических объектах, пока предмет еще не разделен на алгебру и геометрию. Именно в этом возрасте ребенку отводится время на формирование представление о том, как изучаемый объект устроен и как он используется в реальных ситуациях. Исключение этого важного этапа математической подготовки в большинстве случаев оказывается в последствии невосполнимым. Даже опытный репетитор по математике, работая с учеником старших классов, не сможет в полной мере компенсировать недостаток внимания к уравнениям в младших. Можно только дать представление о методах решения или натаскать на заучивание определенных алгоритмов.
Наверное любой репетитор по математике, успевший плотно поработать с учениками 5-6 классов хотя бы пару лет, слышал жалобы от родителей, связанные со снижением успеваемости при переходе в 6 класс. Проблемы начинают возникать даже, казалось бы, с такой простой темой, как уравнения. К удивлению родителей она вдруг неожиданно переходит в категорию трудных. «Мой ребенок всегда хорошо решал уравнения и вдруг перестал их понимать», — часто жалуются родители репетитору математики. «Что нам делать? Я не могу ему донести то, что понимаю сама, а в школе преподаватель толком ничего не объясняет, а только требует», — обычная картина из практики репетитора: родители в панике. Однако, попытка найти спасение нанимая ребенку преподаваеля, не всегда приводит к желаемому результату. Почему?
Репетитор по математике в работе со слабым шестиклассником часто повторяет методологию учебников и опирается на определенные навыки работы с числами и действиями, которые должны быть у школьника сформированны к этому моменту. Но это относится только к способному ребенку. Реальность репетиторской работы такова, что эти навыки дети часто или не получают вовсе или не могут применить их работе с аналогичными, но более сложными конструкциями. И дело не только в том, что этому мало кто учит. Причина кроется еще и в возрастных особенностях работы памяти ребенка и его мышления, в способности рассмотреть простой объект внутри сложного. В большинстве случаев, с которыми репетитору приходится сталкиваться, ученику рано переходить к использованию алгоритмов в более сложных математических объектах.
Почему?
Во-первых, понимание этих аналогий часто еще не успевает сформираться. Во-вторых, механизмы позволяющие переносить эти операции на более сложные объекты могут быть не отработаны на достаточном количестве заданий. В третьих, сами операции и правила, по которым они выполняются, часто забываются.
Глубоким заблуждением многих методистов, репетиторов по математике и школьных преподавателей является мнение о том, что правила нахождения компонентов алгебраических действий помогают ребенку принять решение о том том, сложить ли ему данные числа, или отнять, найти ли разность a-b или b-a. Вспомните себя, помогало ли вам на уроках математике такое правило: чтобы найти вычитаемое, надо из уменьшаемого вычесть разность? Приходится вспоминать названия участников действия, затем текст правила (каждое для своего случая). Пока будет вспоминать текст, — успеет забыть где у него в уравнении стоит уменьшаемое, а где вычитаемое. Начтет вспоминать названия — забудет правило... А еще нужно правильно записать и произвести вычисления. Куда тут до правильного ответа? Укротить бы термины.
Как действует ученик в простом случае и почему он промахивается с подбором действий в более сложных? Дело в том, что к моменту, когда ему необходимо решить уравнение 8-x=3 он, как правило, получает хорошую практику вычислений (если преподаватель по математике дал классу эту практику) и просто узнает знакомую картинку, в которой пропущено одно число. Он может и без правил догадаться, какое число ему поставить вместо икса. И если требуется записать действие для его нахождения, он переберет все возможные варианты с числами 8 и 3 (благо они перед глазами) и выпишет подходящее. Никакими правилами нахождения вычитаемого он в большинстве случаев не пользуется. Это слишком сложно для него.
С некоторым напряжением ученику даются уравнения, нагруженные несколькими действиями, например . Если числа в таких уравнених не очень большие, то в голове пятиклассника реализуется тот же самый алгоритм подбора неизвестного компонента 2x-8 в делении. Этот алгоритм, обычно, опережает подбор действия, с помощью которого получается ответ. Сложности возникают только с тем, что ребенку приходится находить не икс, а некотороый промежуточный результат. Практика моей работы репетитором по математике показывает, что с этим видом непонимния часто удается справиться сравнительно легко. Главная помощь репетитора здесь заключается в своевременном повторении понятия «корень уравнения» и «проверка корня». При этом репетитор должен уделить внимание практическому ходу этой проверки и выделить в ней определенные этапы:1) Берем наугад число для проверки2) Выполняем его умножение на 2, затем потом вычитаем 8 и получаем некоторый промежуточный результат3) делим 42 на него и должно получиться 7.
При такой форме ребенок в 95 % случаев сам скажет репетитору математики, что нужно разделить 6. В этот момент грамотный репетитор обязательно укажет ученику на то, что подобранное число 6 должно получиться в результате вычитания. Останется понять как при вчитани числа 8 получить 6. Репетитору должен поставить новую цель: что вставить вместо икса, чтобы после умножения на 2 и вычитания восьми эта шестерка получилась. Тогда надо решить уравнение, в котором слева уже стоит не , а . Этот момент отдельно выделяется и репетитору обязательно нужно на нем остановиться отдельно. Решая такими путями уравнения ребенок запоминиает поведение чисел. Те взаимосвязи, которые предлагабются ему для заучивания запоминаются в естественном порядке, а именно в процессе деятельности.
Существуют простые, но важные правила работы с методикой:
1) Репетитор по математике должен исключить из текстов своих пояснений стандартные математические термины и шаблонные фразы («значение выражения», «переменная», «делитель», «значение переменной, при которой...»)
2) При подборе уравнения следует не дупустить проникновение в него повторяющихся действий и даже повторяющихся чисел (как начальной в записи самого уравнения, так и во всех дальнейших формах). Иначе ребенок запутается, о каком делении репетитор по математики говорит в конкретный момент и о каком числе 6 идет речь, если она используется дважды.
3) Каждая пара чисел в уравнении на каждом этапе решения должна быть удобной для подбора третьего числа.
В конце 5-го и в начале 6-ого класса понятие числа расширяется. Появляются уравнения с дробями (десятичными и обыкновенными) и вместе с ними приходят главные проблемы. Как теперь решить такое?
Подбор числа и действия затрудняется, так как операции с дробями делаются в несколько этапов. Если раньше ребенок мог распознать, что число а не делится на число b, то теперь уже можно делить друг на друга почти все числа. Сложнее узнать знакомое сочетание и подбирать для него соответствующее арифметическое действие. При достаточном количестве решенного ранее, способные дети дети запоминают алгоритмы и по аналогии применяют их в новой систуации. А что делать отстающим? У многих из них информация о правилах еще успела прочно отложиться в его долговременной памяти. Репетитор по математике истытывает в работе с такими детьми огромные трудности, а ведь решение проблемы лежит на поверхности.
Репетитору необходимо продлить время привычной деятельности ученика при решении уравнений. То есть подбирать действия прежним способом. Для этого преподавателю достаточно обязать (или разрешить) рядом с решаемым уравнением составить любой простенький пример на это же действие, но с натуральными числами. Допустим, надо решить уравнение:
Репетитор просит ученика определить последнее действие в левой части уравнения, составить с его участием любой простенький пример из программы 2-го класса и записать его где-нибудь рядом. В особых случаях можно рекомендовать использовать нижнюю строчку под самим уравнением. Ребенок смотрит, какой учасник последнего действия в исходном уравнении неизвестен, находит его аналог в придуманном примере и по нему подбирает арифметическое действие с соседними числами (благо они перед глазами). Затем просто переносит его на свое уравнение. И так с каждым исключением последнего действия. Полное оформление может выглядеть следующим образом:
Репетитор по математике должен договориться с учеником о том, чтобы в составленных примерах числа не повторялись. Не стоит cоставлять такие примеры: и подобные им ...
Для совсем слабых детей репетитор может заготовить отдельные карточки с уже подобранными примерами на все действия и класть их перед учеником в нужный момент.
Статья из цикла «методики для репетиторов».Колпаков Александр Николаевич, репетитор по математике. Москва, Строгино.
Метки: Методики для репетиторов
ankolpakov.ru
Решение уравнений. 6-й класс
Разделы: Математика
Цели:
- образовательные: показать решение уравнений способом переноса слагаемых из одной части в другую, изменив при этом их знаки; ввести определение линейного уравнения; научить решать линейные уравнения;
- развивающие: развить логическое мышление учащихся, обучать самостоятельно углублять знания, развивать память, внимание, сообразительность, умение рассуждать;
- воспитательные: формировать самостоятельность, воспитывать познавательную активность, внимательность, аккуратность, учится преодолевать трудности, сформировать у учащихся положительный мотив учения.
Оборудование: мультимедийный экран, проектор, презентация.
Ход урока
Здравствуйте, ребята. Помогите мне в начале урока заполнить эту страничку. Ответьте на вопросы и впишите ответы во второй столбик.
- Запись выражения в более коротком виде. (Упрощение)
- Результат вычитания. (Разность)
- Древние счеты. (Абак)
- Предложение, требующее ответа. (Вопрос)
- Великий английский ученый математик, физик, астроном. (Ньютон)
- Самое маленькое натуральное число. (Единица)
- Какое число разделяет положительные и отрицательные числа . (Ноль)
- Вид работы, дающий возможность судить о величине. (Измерение)
- Он и математический, и иностранный… (Язык)
Обратите внимание на только что записанный столбик этого плаката. Прочитайте получившееся слово: уравнение. Что же такое уравнение? (ответы учащихся)
Запишем в тетрадях число и тему урока. И я хочу вам немного рассказать сведения из истории об уравнениях.
Когда же и какие народы начали первыми пользоваться уравнениями? Ещё за 3–4 тысячи лет до н.э. египтяне и вавилоняне, пользуясь таблицами и готовыми выработанными рецептами, умели решать некоторые уравнения. Разумеется, приёмы решения у них были вовсе не такими, как теперь. Греки, унаследовавшие математические знания египтян и вавилонян пошли дальше.
Наибольших успехов в решении уравнений добился выдающийся древнегреческий учёный. Диофант (III век), которого по праву называют «отцом алгебры».
Диофант умел решать очень сложные уравнения, примеряя для неизвестных буквенные обозначения, ввёл специальный символ для вычитания, использовал сокращения слов.
О нём потом писали:
Посредством уравнений, теорем
Он уйму всяких разрешил проблем:
И засуху предсказывал, и ливни –
Поистине его познанья дивны.
В дальнейшем проблема решений уравнений занимала умы всех математиков. О них вы узнаете в старших классах. А вот что писал об уравнениях учёный А. Эйнштейн.
«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно. (Высказывание записано на слайде).
Я хочу, чтобы и мы с вами сегодня научились решать уравнения новым для нас способом. Но для облегчения усвоения новой темы вспомним необходимый для этого материал.
- Вспомним правила знаков при сложении, умножении и вычитании.
- Как открываются скобки, если перед скобкой стоит знак плюс?
- Как открываются скобки, если перед скобкой стоит знак минус?
- Как открываются скобки, если перед скобкой стоит множитель?
А сейчас давайте поиграем, применяя все эти правила. Ваша задача выбрать тему и вопрос, ответить на вопрос и за верный ответ получить баллы. Тем, кто получит 50 и более баллов, я поставлю оценку «5», получившим от 30 до 49 баллов поставлю «4», от 10 до 29 баллов смогут получить «3». Готовы играть? И так начали!
Открывается презентация игра «Проверь себя».
Действия с рациональными числами
- Вычисли: -0,17 – 1,2 + 0,37
Варианты ответов: 1)–1,74; 2)1,74; 3)-1; 4)1;Ответ: - 1 (10 баллов)
- Вычисли: -0,17 – (- 1,2) + 0,37
Варианты ответов: 1) – 1,74; 2) 1,4; 3) 1,74; 4)0,66;Ответ: 1,4 (20 баллов)
- Вычисли: - 4∙2∙(-0,05) + 1,9
Варианты ответов: 1) 2,3; 2) 1,94; 3)1,5;4)5,9;Ответ: 2,3 (30 баллов)
Упрощение выражений
- Упрости выражение: 2,5х – 3х
Варианты ответов: 1) 2,2х; 2) – 0,5х; 3) 5,5х; 4) 2,8х;
Ответ: - 0,5х (10 баллов)
- Упрости выражение: - 0,4∙(- 6,3х)∙2
Варианты ответов: 1) 50,4х; 2) 5,04х; 3) 7,1х; 4) - 5,04х;
Ответ: 5,04х (20 баллов)
- Упрости выражение: 0,3х – 0,4х + х
Варианты ответов: 1) 1,7х; 2) 1,1х; 3) 0,9х; 4) -1;
Ответ: 0,9х (30 баллов)
Раскрытие скобок
- Раскрой скобки и упрости, если это возможно: - (а – 2в) + а
Варианты ответов: 1) - 2в; 2) 2а + 2в; 3) 2в; 4) - 2а – 2в;Ответ: 2в (10 баллов)
- Раскрой скобки и упрости, если это возможно: (2а – 4в + 5)∙(-3)
Варианты ответов: 1) - 6а + 12в – 15; 2) - 6а + 7в – 15;
3) - 6а – 12в – 15; 4) 6а + 12в – 15;Ответ: -6а + 12в - 15 (20баллов)
- Раскрой скобки и упрости, если это возможно: 6х – 0,2(3х - 1)
Варианты ответов: 1) 0,2; 2) 5,4х - 0,2; 3) 5,4х + 0,2; 4) 5,6х;
Ответ: 5,4х + 0,2 (30 баллов)
Решение простейших уравнений
- Реши уравнение: х – 5,6 = 7
Варианты ответов: 1) 1,4; 2) 6,3; 3) 12,6; 4) 4,9;Ответ: 12,6 (10 баллов)
- Реши уравнение: - 0,06х = -1,2
Варианты ответов: 1) 20; 2) 2; 3) -2; 4) -20;Ответ: 20 (20 баллов)
- Реши уравнение: -10х = 2
Варианты ответов: 1) – 5; 2) 5; 3) – 0,2; 4) 0,2;Ответ: - 0,2 (30 баллов)
Физминутка:
А теперь представим, детки,
Будто руки наши – ветки.
Покачаем ими дружно,
Словно ветер дует южный.
Ветер стих. Вздохнули дружно.
Нам урок продолжить нужно.
Подравнялись, тихо сели
И на доску посмотрели.
Мы вспомнили некоторые правила, теперь можно приступать к решению уравнений новым способом. Ребята, как вы думаете, если на чашки весов, находящихся в равновесии, положить равные гири, равновесие сохранится? Это свойство мы можем применить и в уравнениях.
Давайте запишем на доске и в тетрадях решение уравнений
Пример 1. Решим уравнение 4 (х+5)=12Решение. По правилу отыскания неизвестного множителя имеем , т. е. . Это же уравнение можно получить, разделив обе части данного уравнения на 4 или умножив обе части на .Теперь легко найти значение х. Имеем , или ..Число -2 является корнем уравнения и уравнения , так как и .
Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
Пример 2. Решим уравнение (рис. 93).
Решение. Вычтем из обеих частей уравнения по (снимем с обеих чашек весов по две буханки хлеба). Получим . Но , значит . Это уравнение можно получить из данного, если слагаемое перенести из правой части в левую, изменив его знак на противоположный. Решая дальше уравнение , получим и .
Число 2 есть корень уравнения и уравнения , так как и .
Пример 3. Решим уравнение .
Решение. По правилу отыскания неизвестного слагаемого имеем , т.е. . Уравнения и имеют один и тот же корень 6, так как и .
Уравнение можно записать так: . Видим, видим что корень уравнения не изменяется, если перенести слагаемое 5 из левой части уравнения в правую, изменив его знак на противоположный.
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
Пример 4. Решим уравнение .
Решение. Умножим левую и правую части уравнения на 3 для того, чтобы освободиться от дробного коэффициента. Получим . Перенесем с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое Зx из правой части в левую: . Упростим левую часть уравнения: . Теперь разделим обе части уравнения на -2, получим .
Число 18 является корнем данного уравнения , так как верно равенство
Во всех рассмотренных примерах мы приводили данные уравнения к виду , где .
Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным.
На закрепление нового материала, решим уравнения № 1316(а), 1317(а), 1318(а) с комментированием правил
Итоги урока:
Вывод: разные уравнения рассматриваются в математике, но в 6 классе вы имеете дело с простейшими, хотя они, конечно, посложнее тех, с которыми вы, ребята, познакомились в начальных классах и 5 классе. В старших классах и в дальнейшем вы познакомитесь с другими видами уравнений, с решением задач с помощью уравнений и, лучше почувствуете их «силу». Ещё неоднократно убедитесь, что даже в повседневной нашей жизни без уравнений не обойтись. Поэтому, я думаю, что вы запомните сегодняшнее наше занятие.
Оглашение оценок, характеристика работы учащихся.
Задание на дом № 1341(а-в), 1342(а-в), 1334
xn--i1abbnckbmcl9fb.xn--p1ai
Учимся решать уравнения
Урок математики в 6 классе по теме «Уравнения»
Пономарева Ольга Михайловна, учитель математики
Пояснительная записка
Данный урок проведен, по учебнику 6 класса для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С, И. Шварцбурд. — М.: Мнемозина, 2015.
Устная работа направлена на закрепление вычислительных навыков и подготовку к изучению новой темы.
Этот урок является первым из восьми отведенных на изучение данной темы. Главной целью является ознакомить учащихся новым способом решения уравнений с использованием свойств: умножение или деление обеих частей уравнения на одно и то же число и переносом из одной части уравнения в другую.
Данный урок построен в соответствии с принципами здоровьесбережения. Чередование видов деятельности (устный счет, фронтальная, групповая и индивидуальная работа) позволяют сохранить работоспособность детей на хорошем уровне в течение всего урока.
Класс: 6
Предмет: Математика.
Тема: Решение уравнений.
№ урока по данной теме: Первый.
Оборудование: Документ-камера
Цель: Цели урока.
Образовательные:
Развивающие:
формирование умения выделять главное, сравнивать, анализировать и делать выводы;
формирование умения формулировать познавательные задачи, планировать познавательную деятельность;
развивать качества личности – трудолюбие, аккуратность, настойчивость в достижении цели.
Воспитательные:
выработка объективной оценки своих достижений;
формирование честности, как составляющей законопослушания;
формирование ответственности
Формирование умений и навыков решения простейших линейных уравнений при создании условий здоровьесбережения на уроке.
Воспитание взаимоподдержки в ходе совместной деятельности, настойчивости для достижения конечных результатов.
Ход урока
Начать урок словами Жен Жака Руссо «Вы - талантливые дети! Когда – нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремится к их достижению»
В тетради записать дату, классная работа.
На слайде записи: 24х – 56х 5(4а - 7) – (12 + 24а) 16 х = 32 2у + 7у = 8,1 2,7n – (3,8 n – 14,8) 8x = 2x+18.
Разделите записи на две группы. По какому признаку вы это сделали?
2 ученика записывают на доске 2 столбика: (Вахрушева А, Лабутин Н)
1.Буквенные (Алгебраические) выражения
2 Уравнения.
А) Какие действия мы умеем выполнять с буквенными выражениями?
(раскрывать скобки, приводить подобные слагаемые) Упрощаем выражения на доске ( Бурдина, Маргунов, Мига)
Б) Уравнения – решаем самостоятельно. Проверка по готовому решению ученика( через документ - камеру)
- Какие правила применяли для решения?
- Какое уравнение вызвало затруднения?
- Почему?
- Чем это уравнение отличается от тех, которые мы умеем решать?
(содержит неизвестное в обеих частях уравнения).
- Значит тема сегодняшнего урока: Уравнения, содержащие неизвестное в обеих частях
- Какова цель? - Научится решать уравнения
- Что для этого нужно нам сделать? - Вывести правило, которое не изменит корни уравнения, и позволит сделать так, чтобы неизвестные оказались в одной части.
- Запишем 1) сформулировать правило
2) применять правило.
- Какие правила, не меняющие корни уравнения мы знаем?
3. Пословица: Одна голова хорошо, а две лучше.
Как она относится к нашему уроку?
Работа в группах. (3 группы)
(Детям дается задание на карточках. Решают одну и туже задачу, но разными способами).
Один представитель от группы, выходит к доске и объясняет решение.
- Какую закономерность мы увидели во всех решенных уравнениях?
- неизвестное из правой части перешло в левую, только поменяло знак на противоположный.
- Изменились ли корни? Сформулировать правило. Проработать опорный конспект. ( работа в парах)
4. Вернемся к уравнению 8x = 2x+18. Чтобы его решить, что нужно сделать? (На доске решает Лабутин)
5. Закрепим правило при решении уравнения б) 1 – 5х = - 6х + 8.
Анализирум это уравнение, чем оно отличается от предыдущего, чем дополняем правило
__ Переносим не только неизвестные, но и известные, так, чтобы в левой части собрать – неизвестные, а в правой – известные.
Решаем на доске _ (Муленко)
6. Самостоятельно: 10х + 9 = 7х
у+ 2у + 20 = - 3у - 16 Проверка через документ -камеру.
Оценочный лист
Фамилия,имя_____________________________________________________Поставьте знак « + », если вы не допустили ошибки при выполнении действия, и знак « - », если действие выполнено с ошибкой.
| Критерии оценки | Уравнение № 1 | Уравнение № 2 |
Получен правильный ответ
| | |
Правильно выполнен перенос слагаемых из одной части уравнения в другую
| | |
Правильно выполнено приведение подобных слагаемых
| | |
Отсутствуют вычислительные ошибки
| | |
Самооценка работы по критериям. Кто поставил себе 8 « + «, 7, 6 ,5 Молодцы. Обратите внимание на «-« и проработайте соответствующие правила.
7. Вернемся к цели урока. Достигли ли ее?
8. Необходимо еще раз закрепить полученные знания . Домашнее задание: п. 42, правило , 1342 (а, в, д, ж)
Уравнение из ГИА – 9 №1
Электронный дневник, группа «Готовимся к экзаменам»
9 Резерв. 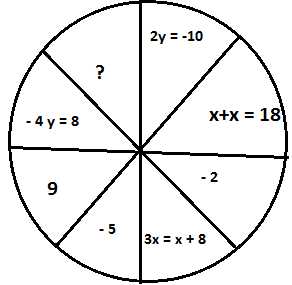
Логическая задача. Как найти неизвестное число?
- Нужно соотнести уравнение и его корни. Решить уравнение 3х = х
+ 8 и найденный корень и будет тем неизвестным, которое нужно найти х = 4.
10 Вернемся к эпиграфу урока. Кто выскажет свои мысли.
Приложения
Опорный конспект по теме «Решение уравнений».
● Если к обеим частям верного равенства прибавить или отнять одно и тоже число, не равное нулю, то получится верное равенство.
● Если обе части верного равенства умножить или разделить на одно и тоже число, не равное нулю, то получится верное равенство.
● Члены уравнения можно переносить из одной части в другую,
изменив их знак на противоположный.

videouroki.net
Тема урока: Решение уравнений 6 класс
Тема урока: Решение уравнений 6 класс
На этом уроке вы узнаете, какие свойства уравнений можно применять при их решении. Вы познакомитесь с определением линейного уравнения и уравнения, сводящегося к линейному. Разобранные примеры и упражнения проиллюстрируют применение рассмотренных правил и позволят связать новый и ранее изученный материал в единое целое.
Первое свойство уравнений. Иллюстрирующий пример. Формулировка
Рассмотрим решение уравнения:
Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 5.
Число 8 – это корень уравнения (1) и корень уравнения (2).
Сформулируем первое свойство уравнения.
Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.
Применение первого свойства уравнений. Упражнения
Пример 1.Умножим обе части уравнения на 9. Тогда коэффициент перед станет целым.
Ответ:
Пример 2.Умножим обе части уравнения на 10. Тогда коэффициенты перед станут целыми.
Ответ:
Пример 3. Разделим обе части уравнения на 20.
Ответ:
Пример 4. Разделим обе части уравнения на 2,1.
Ответ:
Второе свойство уравнений. Иллюстрирующие примеры. Формулировки
Рассмотрим решение уравнения:
Число 4 – это корень уравнения (1) и корень уравнения (2).
Заметим, что уравнение (2) можно было получить, перенеся число +5 из левой части в правую с противоположным знаком:
Сформулируем второе свойство уравнения:
Любое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.
Рассмотрим решение еще одного уравнения: .Вычтем из левой и правой части уравнения . Тогда останется только в левой части.
Число 4 – это корень уравнения (3) и корень уравнения (4).
Второе свойство уравнений можно сформулировать иначе.
Если к обеим частям уравнения прибавить одно и то же число, то корни уравнения не изменятся. Если из левой и правой части уравнения вычесть одно и то же число, то корни уравнения не изменятся.
Применение второго свойства уравнений. Упражнения
Пример 1. Воспользуемся вторым свойством уравнений. Принято слагаемые, которые содержат неизвестное, собирать в левой части уравнения, а остальные в правой.
Пример 2. Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.
Примеры решения более сложных уравнений
Пример 1.
Сначала раскроем скобки.
Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.
Пример 2.
Воспользуемся основным свойством пропорции. Произведение средних равно произведению крайних.
Раскроем скобки в левой и в правой части уравнения.
Перенесем неизвестное влево, а известное вправо.
Линейные уравнения. Определение
Во всех рассмотренных примерах мы приводили уравнение к виду
Уравнения такого вида называют линейными уравнениями с одним неизвестным. Уравнения, которые можно с помощью преобразований привести к такому виду, называют сводящимися к линейным.
Упражнение
При каких значениях переменной значение выражения равно значению выражения ?
Составим уравнение и решим уравнение.
Перенесем неизвестное влево, а известное вправо.
Ответ: при
Текстовая задача
Условие. Рост мальчика – 75 см и еще половина его роста. Найдите рост мальчика.
Решение.1. Пусть (см) – половина роста.Тогда весь рост равен (см),
с другой стороны, весь рост – (см).
Составим уравнение:
75 см – половина роста
2. – весь рост мальчика
Ответ: 150 см.
infourok.ru
Линейные уравнения в 6 классе
После простейших рассмотрим следующие линейные уравнения, решаемые в 6 классе, — уравнения вида ax+b=cx+d.
Алгоритм (план) решения таких линейных уравнений:
неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки.
Рассмотрим примеры решения таких линейных уравнений в 6 классе.
1) 5x-11=2x+7
Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
5x-2x=7+11
(Чтобы лучше запомнить это правило, предлагаю следующую ассоциацию. Есть хозяин, к нему пришел гость. Хозяин у себя дома, в своих домашних тапочках. Гостю надо снять обувь, в которой он пришел — не будет же он ходить в доме в обуви, в которой ходил по улице.
В левой части «хозяин» — слагаемое с переменной, 5x. Оно «у себя дома», поэтому его знак не меняем. «В гости» к нему приходит из правой части уравнения 2x. Его знак меняем на противоположный. В левой части 2x имело знак «+», при переносе знак изменяем на «-«.
Аналогично, «хозяин» правой части — 7. Его знак не меняем, так как это слагаемое остается в правой части. К нему из левой части «приходит в гости» -11. Его знак меняем на противоположный — был «-«, при переносе меняем его на «+».)
3x=18
Это — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:
x=18:3
x=6
Ответ: 6.
2) 12 — 7x=16x + 3
Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
-7x-16x=3-12
-23x=-9
обе части уравнения делим на число, стоящее перед иксом:
x=-9:(-23)
При делении чисел с одинаковыми знаками получается положительное число. Поскольку 9 на 23 не делится, ответ записываем в виде обыкновенной дроби:
Ответ: 9/23.
3) 15x+11=10x-7
Это — линейное уравнение. Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками:
15x-10x=-7-11
5x=-18
Обе части уравнения делим на число, стоящее перед иксом:
x=-18:5
При делении чисел с разными знаками получаем отрицательное число. При делении на 5 ответ записываем в виде десятичной дроби.
x=-3,6
Ответ: -3.6.
4) 54-3y=4y+72
Это — линейное уравнение. Неизвестные переносим в одну сторону, известные — в другую, изменяя при переносе их знаки:
-3y-4y=72-54
-7y=18
Обе части уравнения делим на число, стоящее перед игреком:
y=18:(-7)
При делении чисел с разными знаками получаем отрицательное число. 18 на 7 не делится, поэтому ответ записываем в виде обыкновенной дроби:
Эта дробь — неправильная. Выделяем из нее целую часть:
Ответ:
Позже рассмотрим, как решать в 6 классе более сложные линейные уравнения, в которых требуется раскрыть скобки и привести подобные слагаемые.
www.for6cl.uznateshe.ru
Урок в 6 классе «Основные методы решения линейных уравнений»
1.Мотивация к учебной деятельности. Актуализирует требования к ученику с позиций учебной деятельности. Создает условия для формирования внутренней потребности учеников во включении в учебную деятельность. | – Проверим домашнее задание? – С каким настроением сегодня вы пришли на урок? Прошу определиться и показать соответствующий смайлик. - Ребята, как вы думаете, чем мы будем сегодня заниматься на уроке? – Сегодня мы продолжим изучать тему «Линейное уравнение. Основные методы решения уравнений». -На прошлом уроке мы с вами решили задачу и ответили на вопрос: сколько лет Диофанту? Я попросила вас узнать о нем и ознакомить всех. Кто подготовил информацию? -Как появились уравнения? Кто их придумал? -Многие математики занимались решением уравнений. Одним из них был французский математик, имя которого вы должны узнать сами, решив несколько уравнений. -------------------- Итак, вы узнали это имя-Виет. -Какие сложности возникли при выполнении домашнего задания? -Что нужно знать, чтобы научиться хорошо решать уравнения? ----------------------- -Ребята при решении уравнений часто возникают вопросы на действия чисел с разными знаками. Поиграем? | (2 слайд) С каким настроением я пришел на урок? Я – разный – и натруженный и праздный,И целее – и нецелесообразный,Я весь несовместимый, неудобный, застенчивый и наглый,Злой и добрый. -------------------------------------------------- (3 слайд) УГАДАЙКА. «нелийное внеурание» (открывается на экране.) -------------------------------------------------- (4 слайд) Уравнения для меня важнее, потому что политика - для настоящего, а уравнения – для вечности. А.Эйнштейн -------------------------------------------------- Историческая справка. (о Диофанте) ------------------------------------------------ (5 слайд) Историческая справка. Как появились уравнения? Кто их придумал? 3-4 тысячи лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения. Греки унаследовали знания Египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий ученый Диофант. Большой вклад внес среднеазиатский ученый Мухаммед аль Хорезми (|X век). Уравнения аль Хорезми решает с помощью двух приемов: а) ал-джабр («восстановление»), т. е. перенесение вычитаемых (отрицательных) членов из одной части уравнения в другую; б) ал-мукабала («противоставление») –отбрасывание из обеих частей уравнения одинаковых членов, вроде нашего приведения подобных членов. ----------------------------------------------- (6 слайд) 3х-6=х-8 8х-1=5х+8 8х+9=3х+15 -6х=-4х+16
Т В Е А И -8 -1 1,2 0,5 3 Виет. ------------------------------------------------- (7 слайд)  Это имя-Виет. Это имя-Виет.
Франсуа Виет – великий французский математик. Он положил начало алгебре как науке о преобразовании выражений и решении уравнений в общем виде. Виет был первым, кто ввел буквенное обозначение как неизвестных, так и данных величин. Он создал понятие математической формулы как таковой. Благодаря этому открытию, Виет внес огромный вклад в создание буквенной алгебры. Более подробно вы познакомитесь с трудами Виета в старших классах. (8 слайд) Вопросы к устному зачету. 1.Как раскрыть скобки, перед которыми стоит знак «+»? 2. Как можно найти значение выражения, противоположное сумме нескольких чисел? 3.Как раскрыть скобки, перед которыми стоит знак «-»? 4.Что называют числовым коэффициентом выражения? 5. Чему равен коэффициент выражения ах? А выражения –ах? 6. Какие слагаемые называют подобными? 7. На основании какого свойства умножения выполняют приведение (сложение) подобных слагаемых? 8. Какое уравнение называют линейным уравнением с одним неизвестным? 9. Изменятся ли корни уравнения, если обе части уравнения умножить (разделить) на число, не равное 0? 10. Правило переноса слагаемых из одной части уравнения в другую. -------------------------------------------------- (9 слайд) Разминка: «Да» и «Нет» не говорите. Любое положительное число больше 0 Любое отрицательное число больше 0 Любое положительное число меньше любого отрицательного числа Любое положительное число больше любого отрицательного числа Из двух отрицательных чисел большим будет то, у которого модуль меньше Два противоположных числа всегда равны Если у отрицательное число, то – у >0 Молодцы, ребята. А сейчас поиграем. -------------------------------------------------- (10слайд) Домино 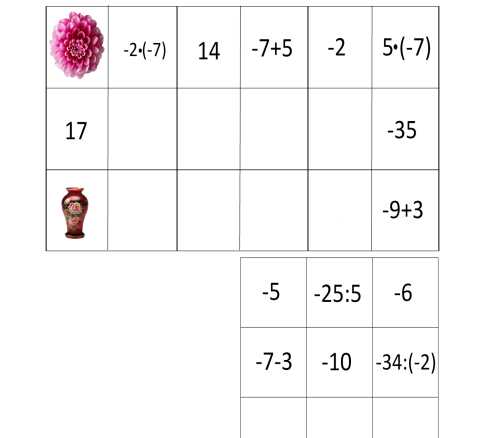 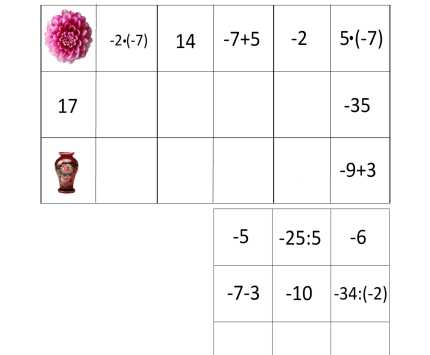 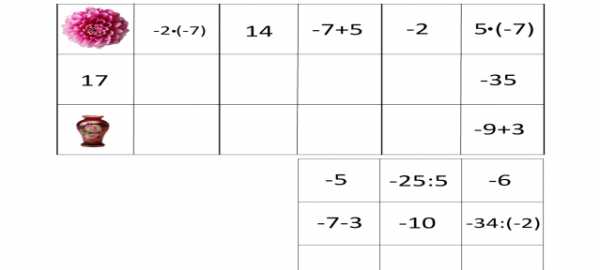 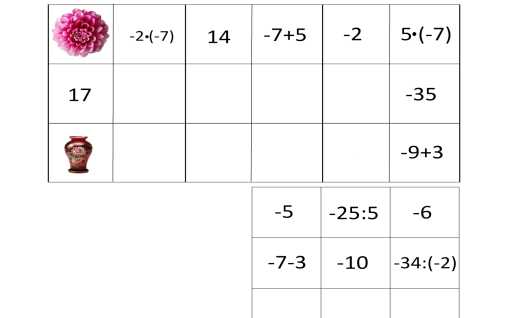 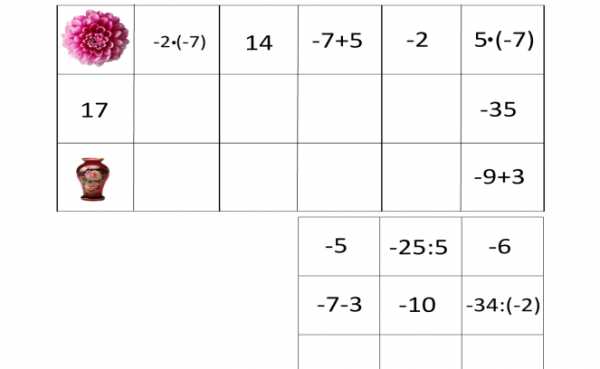 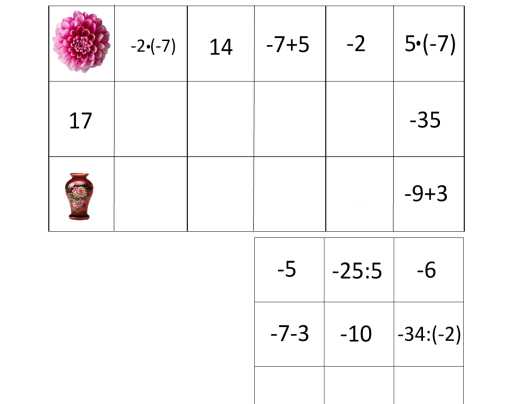 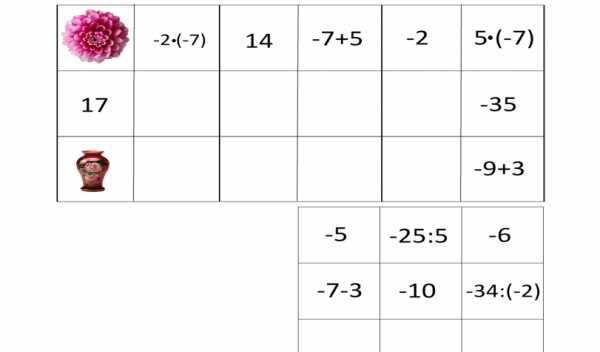 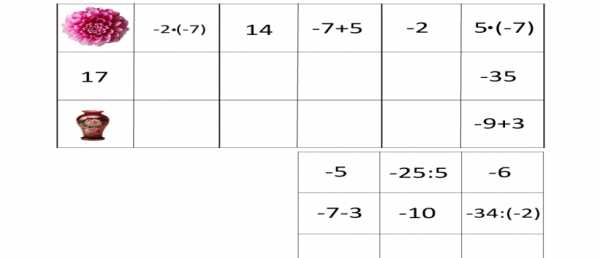
| Отвечают на вопросы учителя, консультанты дают оценку по результатам проверки домашней работы. Выбирают каждый свой смайлик, соответствующий их настроению. Отвечают: -«Линейное уравнение» (по желанию) Ребята рассказывают то, что узнали о Диофанте. Ребята знакомятся с исторической справкой. Решают уравнения. Отвечают: - Виет. -Правила. Работа в парах. Ребята отвечают друг другу на вопросы устного зачета. Верно - руки вверх. Неверно- правая рука вверх (молча). Играем в домино, решая примеры на все действия чисел с разными знаками. | Осознанное и произвольное построение речевого высказывания. | Регулятивные: способность к рефлексии собственной деятельности и деятельности товарищей. Коммуникативные: осознанное и произвольное построение речевого высказывания. Личностные: уметь выделять нравственный аспект поведения. | II. Актуализация знаний и фиксирование индивидуального затруднения в пробном учебном действии; выявление места и причины затруднения. Создает условия для выполнения учащимися пробного учебного действия. Выявляет место и причину затруднения. | ----------------------- -Молодцы. А сейчас ДОМИНО, которое вы сами подготовили. | (11слайд) Найди соответствие: -2х=18 2 7у=-0,07 -10 5х+7=-8 0 -10а=10а-40 -9 -а=5а+12 9 -2(х-3)=-12 1 7(в+2)=-56 -2 -7а+9=2 -0,01 17-3х=17 -3 -------------------------------------------------- Работа в группе | Фронтальная работа. Выполняют устно задание, комментируют действия, отвечают на вопросы. Ответы с места. Играют в домино в группе по 4 человека: решают уравнения. (дают оценку товарищам) | Используют различные приемы проверки правильности выполнения заданий | Регулятивные: уметь определять цель учебной деятельности самостоятельно, осуществлять поиск средств ее достижения. Познавательные: уметь ориентироваться в своей системе знаний уметь преобразовывать информацию из одной формы в другую. Коммуникативные: уметь формулировать собственное мнение и позицию | III. Закрепление с проговариванием во внешней речи. Организует усвоение учениками нового способа действий с проговариванием во внешней речи | - Ребята, какие трудности вызвало у вас решение уравнений. ----------------------- -Ребята, вы повторили алгоритм решения линейного уравнения, а сейчас примените его при решении. ------------------------А сейчас проверьте свое решение по эталону. ----------------------- -Ребята, мы основательно подготовились: повторили правила, алгоритм решения уравнений. -А сейчас самостоятельная работа с последующей самопроверкой. -Вспомним частные случаи, которые встречаются при решении уравнений. | (12слайд) Алгоритм решения уравнения 1. Раскрыть скобки в уравнении, если они есть. 2. Перенести слагаемые с переменной в одну часть уравнения, а слагаемые без переменной - в другую часть уравнения, изменив при этом их знаки. 3. Привести подобные слагаемые. 4. Найти корень уравнения. 5. Выполнить проверку. 6. Записать ответ. -------------------------------------------------- (13слайд) Решение уравнения 1 вариант. 3 (х +2)+9=7(х-3) 2 вариант. 4(х-3) –6= 5(х+4) -------------------------------------------------- (13слайд) ЭТАЛОН 1вариант. 3х+6+9=7х-21 3х-7х=-21-6-9 -4х=-36 х=9 2 вариант. 4х-12-6=5х+20 4х-5х=20+12+6 -х=38 х=-38 -------------------------------------------------- (14слайд) Самостоятельная работа 1вариант. а) 5x-3=4x+7 б)-8a+9=-9a-3 в)(х-8)/7=3/14 2вариант. а)-3х-2=5х+6 б)7а+1=8а+9 в)(х-3)/3=4/15 -------------------------------------------------- (15 слайд) Самопроверка. 1в. 2в. а) 10 а)-1 б)-12 б)-8 в) 9,5 в) 3,8 (16 слайд) Частный случай (если останется время) аХ=0, (a≠0) Х=0 0X=0 Х-любое
3. 0X=а, (a≠0) нет корней | -Трудно: при переносе слагаемых, при раскрытии скобок допускаются ошибки. Проговаривают алгоритм (потом проверяют на экране). Решают уравнение в тетради. Самопроверка по эталону. Проверяют по эталону. (Один ученик комментирует решение). Выполняют задания самостоятельно в тетрадях. Проверяют ответы. Ребята вспоминают уравнения, которые вызвали затруднения. | Умеют переносить слагаемые из одной части уравнения в другую; умеют решать уравнения, раскрывая скобки. | Регулятивные: уметь оценивать и корректировать свои действия в соответствии с учебной задачей. Познавательные: уметь выполнять действия по алгоритму, ориентироваться на разнообразие способов решения задачи | IV. Рефлексия учебной деятельности на уроке. Организует фиксирование нового знания, рефлексию, самооценку учебной деятельности | Даю оценку классу: МОЛОДЦЫ. | - Давайте подведем итоги. Что нового вы узнали на уроке? Чему научились? - Какую цель мы поставили в начале урока? Достигли ли вы цели? -Оцените свою работу в контрольных листах. - Какое сейчас у вас настроение? - Довольны ли вы собой. - Кого бы вы хотели сегодня похвалить из своих друзей и за что? -------------------------------------------------- (17 слайд) Найти коэффициент произведения: 6а(-2) Привести подобные слагаемые: 2а+3а-6а Найти коэффициент произведения: -7m(-3n) Решить уравнение: -3х=9-3х Решить уравнение: 7х=-7х Решить уравнение: 0х=-55 Упростить: -3ав*2с М О Л О Д Ц Ы. -12 -а 21 люб. 0 н. к. -6авс ------------------------------------------------- Рефлексия «Дерево знаний». Домашнее задание: № 1369(а,б),1376 Дополнительно:№1382. | Осуществляют самооценку. Дают оценку товарищу. Решают, отвечают на вопросы, получают слово: МОЛОДЦЫ. Прикрепляют свои смайлики(в виде яблок) на доске, где изображена яблоня. Записывают домашнее задание. | | Регулятивные: уметь оценивать правильность выполнения действия на уроке на уровне адекватной ретроспективной оценки. Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности |
xn--j1ahfl.xn--p1ai



 Это имя-Виет.
Это имя-Виет.


















