 (запись
на доске)
(запись
на доске)Разделы: Начальная школа, Конкурс «Презентация к уроку»
Загрузить презентацию (698,4 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Ход урока
1. Организационный момент.
2. Актуализация знаний.
 (запись
на доске)
(запись
на доске)
– Почему
 (Чем
больше долей, тем меньше каждая доля.)
(Чем
больше долей, тем меньше каждая доля.)
– Что такое проценты? (Части величин, которые выражаются дробями со знаменателем 100.)
– Что вы записали? (Мы записали дроби.) – Что называют дробью? (Дробью называют одну или несколько равных долей частного.) – Назовите знаменатели. (8,10, 8, 12, 6) – Что показывает знаменатель? (Знаменатель показывает, на сколько равных частей делят целое.) – Назовите числители. (1, 5, 4, 5, 5) – Что показывает числитель? (Числитель показывает, сколько равных частей взято.)
Разбейте дроби на две группы. Обратите внимание, что в математике встречаются дроби с одинаковыми знаменателями.
Молодцы!
3. Постановка проблемы.
Сравните дроби (запись на доске)

– Где возникло затруднение? – Почему? (Сравнение дробей.)– Сформулируйте тему урока. (Демонстрируется Слайд 1.)
4. “Открытие” детьми нового знания.
Практическая работа на Слайде 2. (Сравниваются дроби с одинаковыми знаменателями.)
Вывод, сделанный детьми, иллюстрируется на Слайде 3.
Практическая работа на Слайде 4. (Сравниваются дроби с одинаковыми числителями).
Вывод, сделанный детьми, иллюстрируется на Слайде 5.
5. Первичное закрепление.
Физкультминутка для глаз.
6. Самостоятельная работа. (Слайд 13. Сравнить дроби).
7. Слайд 14. Что заметили? Какие величины обозначаются этими буквами?
– Как найти цену? – Как найти количество? – Назовите формулу стоимости.
Заполнить пустые клетки таблицы.
8. Самостоятельная работа. (Слайд15. Решение задачи.)
9. Итог урока. (Слайд 16)
10. Благодарность за урок (Слайд 17).
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Мы делили апельсин. Много нас, а он один
Эта долька для ежа, эта долька для чижа…
А для волка — кожура.
В Школе умных детей Любовь Стрекаловская рассказала, как ввести эту тему и сделать так, чтобы ребенок понял тему и научился решать дроби.
Давайте начнем с самого-самого начала. Представьте себе ребенка, который никогда не видел (а если видел, то не понимает смысла) записи дроби. Он не знает даже этого слова.
Как объснить ему тему и перейти к более сложной части -действию с дробями и решению задач? Как не отбить желание к этой теме? Как связать ее с жизнью?
В школьной программе объяснить дроби предлагается так:
1 Взять яблоко и предложить съесть его двум детям сразу. Они ответят, что это невозможно. Далее необходимо разрезать фрукт и вновь предложить детям. Каждому достанется по одинаковой половине. Таким образом, половинка яблока является частью от целого яблока. А само яблоко состоит из двух частей.
2 Вводим запись. И показываем, что одна половинка — это часть от целого, или 1/2. Значит дробь — это число, которое является частью предмета, меньше, чем один. Также дробь — это количество частей от какой-то вещи.
Далее детям на дом задается выучить определение, и когда введено понятие, начинается период практики.
Однако, по опросам родителей, эта тема является одной из самых трудных для усвоения детьми. Когда обучение происходит по принципу — вот правило — учи — применяй, эффект намного ниже, чем при подходе, который предлагает Любовь Стрекаловская в Школе умных детей.
Ребенок может знать правило, но не понимать, почему это так работает? Почему так записывается?
А отсюда будут ошибки в сравнении 3/11 и 3/17 частей, ошибки в сравнии 2/5 и 1/5 частей
Согласно методике, представленной в школе умных детей, ребенок подводится к новым знаниям и умениям, но все выводы делает самостоятельно. И основной упор при объяснении дел делается на понимание ребенком смысла той или иной темы.
Как эффективно объяснить ребенку дроби?
Детям показывают апельсин и предлагают разделить его на доли.
Один апельсин — это целый предмет. И состоит он из долей.
Мы делили апельсин. Много нас, а он один
Эта долька для ежа, эта долька для чижа…
А для волка — кожура.

На доли можно поделить многое: арбуз, яблоко, шоколад и даже квартиру (комната, кухня, коридор — все это доли квартиры)
Будет замечательно, если ребенок и вы возьмете и физически разделите шоколадку на доли, апельсинку на доли, мандаринку на доли.
Именно на этом шаге мы обращаем внимание на то, что один апельсин — это целый предмет, и его можно обозначить цифрой 1.
Шоколадка — целый предмет, или 1 шоколадка.
Ведь мы шоколадку «разделили» или «раздробили» на части! Апельсин разделили или «раздробили» на доли!
Хорошим подспорьем являются детали ЛЕГО, из которых можно собрать целый прямоугольник и «раздробить» его на части.
На этом шаге можно нарисовать прямоугольник, разделить его на 4 равные части, например, и попросить ребенка закрасить (или отделить) одну часть, две части.

Нарисовать квадрат, раздробить его на 4 части. И попросить закрасить 2 части.
Передаем инициативу думать и делать выводы ребенку и задаем ему вопрос.
— Кто догадается, сколько всего частей в этом предмете?
— На сколько частей мы его раздробли? Разделили?

На четыре!
Вспоминаем, что деление (при делении в столбик, записывается чертой)

Так же и в дробях. Черта обозначает деление! На сколько частей мы разделили данный прямоугольник?
Так и напишем, делили на 4

А теперь сколько частей мы взяли? Закрасили?

А давай возьмем две части? Как закрасим? Как напишем?
Далее необходимо разделить прямоугольник на другое количество частей, и предожить взять две части. Спросите ребенка, как это показать?
Как записать, что взяли 2 части из 5?
Вспоминаем, что надо поставить черту (разделить), на 5 частей. И взять 2 части

Для этого шага пригодится шоколадка.

Можно спросить, сколько шоколадок? Одна.
— На сколько долек мы раздробили шоколадку? — На 8 долек.
— Как записать шоколадку, но с помощью дроби? На сколько разделили?
— На 8 частей.
— А в целой сколько частей?
8 частей или 8/8 целая шоколадка.
Далее возвращаемся и записываем целым предметом другие разделенные до этого предметы.
Отломите три кусочка, дайте ребенку. Сколько дали? 3. От скольки? от 8!
Запишем полученную дробь 3/8!
Детали лего, полоски, прямоугольники, шоколад, конфеты, жвачки с дольками и т.п
В ход идет любой подручный материал.
Но одно условие — дробить надо на равные части.
Дети очень любят играть с дольками из пачки жвачки.

10/10 — это целая упаковка жвачки
2/10 — как в рекламе
6/10 — 6 долек из пачки жвачки
Шаг 6. Разбираемся в терминологии
И снова задаем ребенку вопросы и помогаем найти ответы.
— В числе 3/8 что обозначает число 8?
— На сколько поделили!
— Что означает число 3?
— Сколько взяли!
— Правильно, число долек, которое взяли. Его еще называют числитель.
Предложите ребенку две дроби:

И поставить знак > в ту сторону, какая дробь больше
Для выполнения задания лучше взять шоколадку, в которой есть 20 долек.
И взять 2 дольки (приложить к дроби 2/20) и 4 дольки (приложить к дроби 4/20). Спросить, где больше. Глядя куда ворона откроет рот?
Техника ворона, благодаря которой детям можно объяснить тему сравнения чисел представлена в видео ниже:
Когда ребенок справится с этим заданием и подобными, усложняем задачу.
Пишем другой пример:

Вспоминаем шоколадку.
Взяли и там и там по две части. Но в первом случае, раздробили шоколадку на 20 долек, а во втором — эту же шоколадку, на 10 долек.
Конечно, лучше всего проделать это на практике.
Подобные сравнения — самая сложная тема для детей на этапе знакомства с темой дроби. Им кажется, что если число 20 больше, то и дробь тоже.
И именно здесь скрывается подводный булыжник.
Попробуйте и практикуйте с шоколадкой такие примеры.
Ребенок, при соблюдении последовательности шагов при объяснении темы, а так же, если вы не будете давать готовые решения и ответы, схватит тему и поймет ее.
А именно это является самым ценным.
Такой подход называется — проблемным обучением, или развитием в ребенке критического мышления. Когда мы ребенку не даем правило или ответ, но помогаем вывести его самому.
Ведь ребенок сам назвал, что шоколадку «раздробили», а значит узнал слово «дробь».
Сам вспомнил, как записывать деление чертой.
Сам ответил, что в примере 3/8, тройка — это число долек, которые «Взяли», числитель
Сам понял, что 8 — это на сколько поделили.
В школе умных детей вы найдете простые и понятные видео-ответы на все темы, получите уникальный опыт учителя и пошаговую инструкцию, как и что объяснить ребенку.
Чтобы дети, которые не понимают ту или иную тему или которым не повезло с учителем, имели возможность полюбить обучение, учиться у лучших учителей (в том числе по английскому у носителей языка)
Чтобы родители, которые совсем не педагоги, и не знают методик преподавания, имели инструмент, позволяющий легко и просто учить ребенка на семейном обучении или стать ребенку грамотным помощником дома, не тратя бюджет семьи на репетиторов.
Школа умных детей — это инвестиция, которая окупится уже в первые месяцы обучения ребенка.

Что вы получите?
Уроки по русскому и математике на 4-6 минут, это объяснение для родителей, как объяснить ребенку ту или иную тему, с какими сложностями можно столкнуться. Но многие наши родитетели напрямую включают уроки деткам (3-4 класс смело), а в 1-2 классе вместе смотрят и потом выполняют задания.
Уроки по английскому языку — это напрямую уроки для детей с отдельными поясняющими уроками и материалами для родителей.
Так же в школе открыта база знаний с техниками эффективного обучения: как учить стихотворения, определения, пересказывать текст, повысить скорость чтения и другие инструменты
И многое, много другое.
Сейчас в школе около 500 уроков на все сферы школьной жизни.
Доступ октрывается ко всем урокам начальных классов (1-4 классы) до мая 2019 года (1.5 учебных года вместо 1) при оплате в ноябре-декабре 2017 года
Получить объяснение всех тем начальной школы простым и эффективным языком
Получить объяснение всех тем начальной школы простым и эффективным языком








Наша система позволит вам отыскать самую короткую дорогу на пути к воспитанию умного, счастливого, успешного, талантливого ребенка, верящего в себя.
Вы получите четкую систему действий, которая заиграет ярко, живо и с любовью.
Станьте участником Школы умных детей уже сегодня и получите эффективную систему обучения ребенка.
Стать участником школы умных детей
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Нравится Загрузка...
gladtolearn.ru
Дата: 13 марта 2014 Автор: Алина Рубрика: Правила

Когда же в школе проходят дроби?… Класс 4-й, кажется, или чуть раньше. Сложная тема, ничего не скажешь. Но вот интересно: жизнь знакомит ребёнка с дробями гораздо раньше школьной программы! Первый раз это происходит, когда хочется поделиться с другом конфетой, а она всего одна. И вот ребёнок уже знает, что такое «половина» и что значит «пополам». А юные музыканты, придя в первый класс музыкальной школы, сталкиваются с дробями буквально на первом уроке: целые ноты, половинные, четвертные, «восьмушки». И на примере яблока малышам объясняют, что это такое. Стало быть, можно начинать первое знакомство с дробями пораньше. Почему бы и нет? Если это будет наглядно, доступно, просто, то ребёнок усвоит эту премудрость легко и играючи.
Договоримся сразу, что дробь — это часть целого, меньше единицы. На сколько частей мы будем делить целое? А это как договоримся. Что будем считать единицей? Тоже как договоримся. Вот такие они сговорчивые, эти дроби. И ещё нужно запомнить одну вещь: то число, на сколько частей мы решили делить целое — это знаменатель, сколько этих частей мы взяли — это числитель.
Например, вот такая история. На траве лежат 3 яблока, ёжик взял только 2. За целое (единицу) мы возьмём все яблоки — весь урожай. Но их у нас 3, значит, наш урожай делится на 3 части. 3 — это знаменатель. Весь урожай (единица) — это 3/3, а каждое яблоко — это 1/3 урожая. Раз ёжик взял 2 яблока, значит, он взял 2/3 урожая!
А можно взять лего, такой любимый многими детьми конструктор. Мы ведь давно заметили, что все его элементы разные по размеру, правда? И на каждой детальке разное количество точек-«пупырышек». Посчитаем — вот одна, две, четыре, шесть и даже восемь.
Давайте за целое (единицу) будем считать «кирпичик» лего с восьмью точками. Для начала сравним его с другими. Сколько деталек лего с 4-мя точками нужно взять, чтобы получился наш «кирпичик»-единица? Правильно, две. Значит, одна деталька с 4-мя точками — это 1/2 нашей «единицы». А сколько деталек с двумя точками нужно взять, чтобы получить целое? Верно, четыре. Стало быть, одна такая деталька — это 1/4. А деталь с одной точкой -это 1/8, потому что таких деталек понадобится аж 8 штук, чтобы получилось целое. Теперь задачка посложнее: перед нами элемент с шестью точками. В нём помещается 3 «четвертинки», а если добавить к нему ещё одну — получится целое (единица). Итак, вот и первый пример готов: 3/4+1/4=4/4 или же 1 (если числитель и знаменатель равны, значит, это единица!)
Это далеко не единственный эксперимент, который можно провести с лего. С дробями-то можно договориться о многом. А что, если мы то же самое, будем считать не четвертями, а восьмыми? И знаменателем у нас будет 8? Смотрим на картинку: единица — «кирпичик» с восьмью точками. 1/2 — это получается 4/8, а 1/4=2/8. А это уже история о том, как можно сокращать дроби. Но эта тема, действительно, может немножко подождать!Автор: Юлия Белка
(Visited 11 195 time, 2 visit today)
Оцените статью: Поделитесь с друзьями!Метки:
shkolabuduschego.ru
Разделы: Начальная школа, Конкурс «Презентация к уроку»
Загрузить презентацию (1,9 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели:
Тип урока: комбинированный с компьютерной поддержкой и элементами здоровьесберегающих технологий.
На уроке с компьютерной поддержкой используются следующие формы обучения:
Оборудование: мультимедиа проектор, карточки для практической работы, фломастеры (карандаши), заготовка-круг, ножницы.

План урока
I. Организационный момент.
II Устный счет.
III. Сообщение темы урока. Постановка учебной задачи.
IV. "Открытие" новых знаний.
V Первичное закрепление. Практическая работа
VI. Решение тренировочных упражнений.
V. Итог урока.
1. Организационный момент.
-- Итак, начинаем урок математики. Посмотрите друг другу в глаза, улыбнитесь, мысленно пожелайте друг другу добра, удачи. Работайте старательно и вас обязательно ждёт успех.
- Ребята, сегодня на уроке вы должны открыть новое знание, но, как вам известно, каждое новое знание связано с тем, что мы уже изучили. Поэтому, начнём мы с повторения.
Перед тем, как приступить к работе вспомним, какие правила мы должны соблюдать на уроке? (Учитель выслушивает ответы детей) (слайд 2)

ПРАВИЛА:
II. Устный счёт (слайд 3)
1. Вычисли удобным способом:
37 +85 + 115 + 33
2. Миша нашёл а грибов, а Паша в 4 раза больше. Сколько грибов нашли мальчики? На сколько грибов Паша нашёл больше?
3. Прочитай число: 198400002. Сколько в нём сотен? Сколько единиц 1 класса?
4. Ленту длиной 2 м разрезали на 5 частей. Какой длины оказалась каждая часть?
5. 1 : 2= ? - Как 1 разделить на 2? (Ответы дете0й
- Итак, какая проблема у нас с вами возникла?
III. Сообщение темы урока
Тема сегодняшнего урока - "Доли и дроби" (слайд 4)
Цели:
- Нам часто в жизни приходится делить целое на части. А сегодня в этом нам поможет семья Долиных. (слайд 5) Давайте я вам расскажу о семье Долиных. Бабушка (слайд 6) очень любит печь пироги и печенье. Дедушка гордится своим садом. Папа с мамой работают на ферме, в основном они выращивают коз, в этом им помогают их дети Дробик и Долюша.
Дробик и Долюша проголодались, а на обед у них только один песочный пирог. Бабушка куда-то ушла и поделить его некому. Поделите его сами.
Дробик: Я разрешаю тебе, Долюша поделить пирог при условии, что я выберу свою часть первым (слайд 7.) Долюша режет пирог пополам. Он следит за тем, чтобы оба куска были одинаковыми.
Долюша разрезала пирог пополам. (слайд 8) Половина - это доля! Но как только мы её запишем вот так ?, доля станет называться дробью. Числа, которые больше 0, но меньше 1, называются простыми дробями . Этот кусок уже не целое, то есть меньше 1, но и не 0, ведь он есть.
- А после пирога ребята съели апельсин (слайд 9)
IV. "Открытие" новых знаний.
Число под чертой указывает на сколько равных частей был поделен предмет. Число над чертой показывает, сколько таких частей берется.
Дробь - это одна или несколько равных долей, записанных с помощью двух чисел, разделенных чертой. - Как же они называются? ( уч-ся ищут в классе ответ на карточках)
 , где - m
числитель, а n - знаменатель. (слайд 10)
, где - m
числитель, а n - знаменатель. (слайд 10)
Число под чертой называется знаменателем, а число над чертой называется числителем.
Папа с мамой тоже проголодались. Дробик и Долюша, поделитесь с ними. Как вы поступите? Значит надо поделить пирог на 4 части (слайд 11). Четверть - это доля. Как напишем это число? Почему?
(слайд 12)

Игра "Числитель-знаменатель"
Чтобы запомнить, что такое числитель и знаменатель и не путать их поиграем в игру. Если я называю числитель, поднимаем руки вверх - показываем, что он записывается сверху. Если я называю знаменатель, показываем, что он пишется внизу. Если показываю черту дроби, складываем руки горизонтально
Бабушка Доля испекла пиццы. И ей прислали заказы на них. Давайте поможем разделить пиццы (раздать пиццы- круги и заказы на них. Ученики делят на 4 и 8 частей)
Сравнение дробей (вырезают)
- У кого больше? Что мы видим?
Дети сравнивают в парах способом наложения. Учитель на модели
Вывод: чем больше знаменатель, при одинаковом числителе, тем меньше дробь, чем меньше знаменатель, при одинаковом числителе, тем больше дробь.
Вывод : чем меньше числитель, при одинаковом знаменателе, тем меньше дробь, чем больше числитель, при одинаковом знаменателе, тем больше дробь.
Давайте сравним доли (слайд 13): Чем больше долей, тем меньше каждая часть. (1/9 1/3)
(слайд 14) (сравнение дробей с одинаковым числителем)
Пауза. (стоя) Закройте глаза. Представьте, что ваш носик вырос, как у Буратино. Обмакните его, как в сказке, в чернила и начертите носом с движением головы в воздухе квадрат, разделите его на 4 части, закрасьте 3/4 своим любимым цветом.
(слайд 15) (Нахождение доли числа) (1/9 от 72 м, 1/8 от 96 м, 1/5 от 90 ц, 1/6 от 84 ч, 1/7 от 280 кг, 1/4 от 320 с)
(слайд 16) Яблоко вести 300 г. Сколько весит 1/6 этого яблока?
Арбуз весит 8 кг. Сколько весит половина арбуза?
V. Первичное закрепление. Практическая работа
А теперь давайте посмотрим и запишем, какая часть дроби закрашена (слайд 16).
VI. Решение тренировочных упражнений.
1. Ну а теперь несколько задач (слайды 17 - 21)
2. Теперь давайте попробуем найти число по доле. № 225 (Учебник "Математика-4", М.И.Моро,2008)
3. Попробуем выполнить сложение и вычитание дробей (слайд 22):
а) Картофель занимает 3/7участка, а помидоры 1/7 участка. Какую часть участка занимают помидоры и картофель?
б) За два дня засеяли 10/11 поля. В первый день засеяли 4/11 поля. Какую часть поля засеяли во второй день?
в) Бабушка принесла апельсины. Дробик получил 3/7, а Долюша 2/7 части всех апельсинов. На сколько Дробик получил больше апельсинов, чем Долюша?
V. Итог урока. (слайд 23)
- Сегодня вы получили оценки 20/4 и 20/5. Сколько это?
- Вы, действительно, смогли доказать, что дроби не поставили вас в трудное положение.
Закрепление - крюки Эдиссона
ДОМАШНЕЕ ЗАДАНИЕ

| Фигура | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Закрашено | ||||||||||
| Незакрашено |
Окончен урок, и выполнен план. (слайд 24)
Спасибо, ребята, огромное вам.
За то, что упорно и дружно трудились, И знания точно уж вам пригодились
xn--i1abbnckbmcl9fb.xn--p1ai
Выходим на битву с домашним заданием по математике! Враг — непокорные дроби. Программа 5 класса. Стратегически важная задача — объяснить ребенку дроби. Поменяемся ролями с учителем и попробуем сделать это «малой кровью», без нервов и в доступной форме. Обучить одного солдата куда легче, чем роту…
 ria.ru
ria.ru
Не ждите, пока ребенок пойдет в 5 класс и встретится с дробями на страницах учебника по математике. Ответ на вопрос «Как объяснить ребенку дроби» рекомендуем поискать на кухне! И сделать это прямо сейчас! Даже если вашему малышу только 4-5 лет, смысл понятия «дроби» он в состоянии уяснить и даже может научиться простейшим действиям с дробями.
Мы делили апельсин. Много нас, а он одинЭта долька для ежа, эта долька для чижа…А для волка — кожура.
Помните стихотворение? Вот самый наглядный пример и самое эффективное руководство к действию! Объяснить ребенку дроби проще всего на примере еды: режем яблоко на половинки и четвертинки, делим пиццу между членами семьи, разрезаем буханку хлеба перед обедом и т.п. Главное, перед тем, как съесть «наглядное пособие» не забудьте озвучить, какую часть от целого вы «уничтожаете».
Сделайте акцент на том, что ЦЕЛЫЙ апельсин (яблоко, шоколадка, арбуз и пр.) — это 1 (обозначаем цифрой 1).
Апельсин или шоколадку мы делим, можно еще сказать «дробим» на несколько частей.
Покажите ребенку хорошо знакомый предмет — линейку. Объясните, что между числами есть промежуточные значения — части.
 i.ytimg.com
i.ytimg.com
Смысл понятия «дроби» и правильную запись легко показать на примере конструктора. В числителе НАД чертой пишем какая часть, а в знаменателе ПОД чертой — на сколько таких частей было разделено целое.
 gladtolearn.ru
gladtolearn.ru

spacemath.xyz
Обязательно на наглядном примере покажите разницу между дробями с одинаковым числителем, но разными знаменателями.
 gladtolearn.ru
gladtolearn.ru
На примере 4-х квадратов одинакового размера покажите, как можно разделить их на одинаковое/разное количество частей. Пусть ребенок сам разрежет ножницами бумажные заготовки, а затем запишет при помощи дробей результаты.
 gladtolearn.ru
gladtolearn.ru
Вспомните квадрат и то, как мы делили его на 4 части. Квадрат — это целое, мы можем записать его как 1. Но как записать в виде дроби: что в числителе, что в знаменателе? Если мы делили квадрат на 4 части, то целый квадрат, это 4/4. Если мы делили квадрат на 8 частей, то целый квадрат это 8/8. Но это все равно квадрат, т.е. 1. И 4/4, и 8/8 — это единица, целое!
Чтобы ученик 5 класса понял тему «Дроби» и научился выполнять вычисления с дробями, заглянем в методику. Нам, родителям, важно понимать, как объясняет детям дроби учитель в школе, иначе мы можем окончательно запутать своего «солдата».
Дробь — это число, которое является частью целого предмета. Оно всегда меньше единицы.
Пример 1. Яблоко — это целое, а половинка — одна вторая. Она же меньше, чем целое яблоко? Половинки делим еще раз пополам. Каждая долька — одна четвертая от целого яблока, и она меньше, чем одна вторая.
Дробь — это количество частей от целого.
Пример 2. Например, в магазин одежды завезли новый товар: 30 рубашек. Продавцы успели разложить и развесить лишь одну треть всех рубашек из новой коллекции. Сколько рубашек они развесили?Ребенок легко устно посчитает, что треть (одна третья) — это 10 рубашек, т.е. 10 развесили и вынесли в торговый зал, а еще 20 осталось на складе.
ВЫВОД: Дробями можно измерять все, что угодно, не только куски пиццы, но и литры в бочках, поголовье диких животных в лесу, площадь и т.п.
Приводите самые разные примеры из жизни, чтобы ребенок 5 класса понял СУТЬ дробей: это поможет в дальнейшем в решении задач и выполнении вычислений с правильными и неправильными дробями, и обучение в 5 классе будет не в тягость, а в радость.
Как убедиться, что ребенок усвоил, что в записи дробей обозначают числа в числителе и в знаменателе?
Пример 3. Спросите, что значит 5 в дроби 4/5?
— Это на сколько частей поделили.— А что значит 4?— Это сколько взяли.
Сравнение дробей — самая, пожалуй, сложная тема.
Пример 4. Предложите ребенку сказать, какая дробь больше: 3/10 или 3/20? Кажется, что раз 10 меньше 20, то и ответ очевиден, но это не так! Вспомните про квадраты, которые мы разрезали на части. Если два одинаковых по размеру квадрата разрезать — один на 10, второй на 20 частей — ответ очевиден? Так какая дробь больше?
Действия с дробями
Если вы видите, что ребенок хорошо усвоил смысл записи в виде дроби, можно переходить к простым арифметическим действиям с дробями. На примере конструктора можно сделать это очень наглядно.
Пример 5.
 edinstvennaya.ua
edinstvennaya.ua
Пример 6. Математическое лото на тему «Дроби».
 www.kakprosto.ru
www.kakprosto.ru
Уважаемые читатели, если вы знаете другие эффективные методики, как объяснить ребенку дроби, делитесь в комментариях. С радостью пополним нашу копилочку дельных школьных советов.
rastishka.by

Разделы: Начальная школа
Цели:
1. Повторить и закрепить умения читать и записывать дроби; сравнивать дроби с одинаковыми знаменателями и дроби с одинаковыми числителями.
2. Развивать математическую речь, внимание, память, логическое мышление.
3. Воспитывать целеустремлённость, бережное отношение к своему здоровью, любознательность.
Ход урока
1. Орг. момент. Настрой на урок.
- Урок математики я начну словами французского философа Ж. Ж. Руссо: “Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремится к их достижению…”.
- Я желаю вам уже сегодня на уроке убедиться в словах Ж. Ж. Руссо. Удачи! В добрый путь за знаниями!
2 Актуализация знаний. Постановка проблемы.
- Чтобы определить тему нашего урока, мы должны выполнить задание.
- У каждого из вас на партах лежат полоски. Разделите полоску на 4 равные части. Покажите 3 части. Графическую модель какого числа мы с вами получили? (3/4).
- ____________ запиши на доске это число. (3/4)
- Как называется это число? (Дробь)
- Какова тема нашего урока? (Дроби)
- Цель нашего урока: повторить и закрепить умения читать и записывать дроби, сравнивать дроби с одинаковыми знаменателями и дроби с одинаковыми числителями; развивать внимание, память мышление.
- Для чего изучаем дроби? Как и где это может пригодиться нам в жизни?
3. Работа по теме урока.
- Итак, дроби.
- Что такое дробь? (Дроби – это числа, выражающие части единиц счёта или измерения. Дробь – это одна или несколько равных долей, записанных с помощью двух натуральных чисел, разделённых чертой)
- Как называется число, записанное под чертой? (Знаменатель)
- Что показывает знаменатель дроби? (Знаменатель дроби показывает на сколько частей разделили целое)
- Как называется число, записанное над чертой? (Числитель)
- Что показывает числитель дроби? (Числитель показывает сколько таких частей взяли)
- Найдите на доске дроби. (Дети называют карточки с дробными числами, а я выстраиваю их в один ряд)
- Какое число оказалось лишним? Почему? (8 – натуральное число, а остальные дробные числа)

- Что общего между этими числами? (Дробные числа с одинаковыми знаменателями)
- Как знак какого действия понимают черту дроби? (Знак деления)
- Сегодня на уроке мы познакомимся с великим немецким математиком, который имеет непосредственное отношение к дробям. Оказывается, в древности для основных дробей, которые были в обиходе, существовали индивидуальные знаки, а остальные дроби получались из основных дробей с помощью арифметических действий. Вот как, например, обозначались некоторые дроби в древнем Египте:
половина –
треть –
четверть –
шестая часть –
Поскольку три четверти составляют в сумме половину и четверть, то эту дробь записывали так:
- Современная система записи дробей с числителем и знаменателем была создана в Индии, только там не писали дробной черты, а кто же значительно упростил эту запись и ввёл дробную черту, мы узнаем, выполнив верно следующее задание.
- В классе 3 ряда, значит, будет 3 команды. Ваша задача расположить карточки с дробными числами в порядке убывания. Расположив верно, первый ряд узнает - фамилию, второй ряд – имя, немецкого математика, который ввёл данный знак деления. А задача третьего ряда – соединить дроби с их графическими моделями.
- А к доске выходит _________________. Твоя задача расположить эти дроби в порядке возрастания и соединить их с графическими моделями.
- Задания всем понятны? Итак, приступаем.

- А теперь проверим как справились с заданием первый и второй ряд. Первый ряд – прочитайте, какое слово у вас получилось? Второй ряд? Проверим.
Лейбниц Готфрид Вильгельм, немецкий, математик, физик и изобретатель, юрист, историк и языковед, родился в 1646 г. в Лейпциге в семье профессора местного университета. В 15 лет в этот университет поступил Лейбниц и стал изучать право, философию и математику. Окончив университет, он получил степень доктора права.
В 1711, 1712 и 1716 гг. встречался с Петром I, разработал ряд проектов по развитию образования и государственного управления в России.
Лейбниц был талантливым изобретателем; он проектировал оптические приборы и гидравлические машины, работал над созданием “пневматического двигателя”, изобрел первую и уникальную для того времени счетную машину.
И он же ввёл дробную черту, как знак деления.
- Можем ли мы про этого человека сказать, что он умел ставить перед собой цели и путём усердного труда добиваться их. И я думаю, что вы согласитесь со мной, что только целеустремлённый человек может многого добиться в своей жизни.
- Какие знания вам понадобились, чтобы расположить эти дроби в порядке возрастания. (Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше)
- Ребята, а что общего между этими числами? (Дробные с одинаковыми числителями)
- Какое правило ты вспомнил, когда выполнял это задание? (Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше)
- Прочитайте слово, которое получилось у __________________. (Логист)
- Как думаете, что означает это слово? От какого слова образовано слово логист?
- Логист – это современная профессия.
Ставя перед собой цель, надо уметь верно спланировать свои действия для её достижения, построить правильный и чёткий план. Хорошо с этим справляются “логисты”.
Логист – это человек, который должен рассчитать схему, наиболее выгодную для развития того или иного проекта и при этом сэкономить везде, где это возможно.
- А для этого надо со школьной скамьи развивать логику, мышление, быстроту и точность вычислений, чем мы с вами и занимаемся на уроках математики.
4. Решение задачи на логику.
- А теперь давайте проверим вашу логику. Послушайте внимательно задачу.
У Оли и Яны два одинаковых яблока. Оля съела 3/6 своего яблока, а Яна 1/4 часть своего яблока. Кто из девочек съел больше?
После ответов детей.
- Сейчас вы воспользовались логикой, догадкой. В старших классах вы научитесь сравнивать такие дроби.
5. Самостоятельная работа.
- А теперь мы покажем свои умения сравнивать дроби, основываясь на правилах. Поработаем с учебником. Откройте страницу 92, найдите №10.
- Рассмотрите эти дроби.

- Разбейте эти дроби на две группы. (Дроби с одинаковыми знаменателями и дроби с одинаковыми числителями)
- Какое правило нужно знать, чтобы сравнить дроби с одинаковыми знаменателями? (Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше)
- По какому принципу будем сравнивать дроби с одинаковыми числителями? (Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше)
- Выполните задание самостоятельно.
- Проверим.
- Кто выполнил без единой ошибки? Кто допустил 1 ошибку?
Физкультминутка.
5/3 присели
6/8 наклоны вправо - влево
7/9 хлопки в ладоши
4/7 прыжки на месте
- Продолжаем урок.
6. Блиц-турнир.
- А сейчас у нас “блиц – турнир” по задачам. Мы повторим с вами два важных правила, знание которых нам пригодится сегодня на уроке и вообще в нашей повседневной жизни.
1. На территории нашего города и района 110 крупных предприятий, 2/5 из которых составляют промышленные. Сколько промышленных предприятий в нашем городе и районе?
110:5*2=44 задача на нахождение части числа
- Как найти часть числа? (Чтобы найти часть числа, выраженную дробью, надо целое число разделить на знаменатель и умножить на числитель дроби)
2. В нашем городе и районе 108 учреждений культуры 4/9 из которых составляют библиотеки. Сколько библиотек на территории нашего города и района?
108:9*4=48 задача на нахождение части числа.
- Как найти часть числа? (Чтобы найти часть числа, выраженную дробью, надо целое число разделить на знаменатель и умножить на числитель дроби)
3. Сколько спортивных площадок в нашем городе и районе, если 4/10 их составляют 88 площадок?
88:4*10=220 задача на нахождение числа по его части
Как найти число по его части? (Чтобы найти число по его части, выраженной дробью, надо разделить эту часть на числитель и умножить на знаменатель дроби)
- А для чего нужно столько спортивных площадок в нашем городе и районе? (Чтобы укреплять своё здоровье)
- Какие два важных правила мы повторили при решении этих задач?
- Возьмите квадраты. Они зелёного цвета. Зелёный цвет – это цвет жизни. Дизайнеры, психотерапевты, создатели рекламы утверждают, что он успокаивающий, способствует жизни, росту, гармонии, объединяет людей с природой, помогает быть ближе друг к другу, развивает силу воли, постоянство, зелёный цвет очень благотворно влияет на наши глазки.
Гимнастика для глаз. (Музыка)
- Поэтому мы сейчас выполним гимнастику для глаз. Посмотрите на квадрат. Обведите его глазками по часовой стрелке. Против часовой стрелки. Проведите глазками по диагонали от левого правого верхнего угла к нижнему левому углу. От левого верхнего угла к нижнему правому углу. Разделите невидимыми линиями квадрат на 4 равные части. Продолжаем смотреть на квадрат. Поморгайте часто глазками. Зажмурьтесь. Откройте глаза.
7. Анализ и решение задачи.
- Наши глазки отдохнули и мы продолжаем работу. Ваша задача с помощью этого квадрата показать дробь 6/9.
Проверка.
- К доске выйдет _____________. Покажи, как ты это сделал. Объясни.
Остальные сравните. (Сложил на 9 равных частей, 6 частей заштриховал)
- Какая площадь в квадрате больше: заштрихованная или незаштрихованная? Почему? (Заштриховано шесть частей, а не заштриховано 3 части, значит заштрихованная часть больше)
- А давайте найдём площадь заштрихованной части.
- А мы умеем находить площадь? (Да)
- Площадь этой фигуры сможете найти? (Да)
- А площадь этой фигуры? (Нет)
- В математике есть общее решение для всех случаев. Обозначьте числом заштрихованную часть. (6/9)
- Как найти часть числа, выраженную дробью? (Чтобы найти часть числа, выраженную дробью, надо целое число разделить на знаменатель и умножить на числитель дроби)
- Вот это правило мы применим, выполняя это задание.
- А у нас есть это целое число? (Нет)
- Чем оно является? Что нужно взять за целое число? (Площадь прямоугольника)
- Сможем ли мы её найти? (Да)
- Как?
- А теперь основываясь на правило, что мы должны сделать далее?
- Как найти часть числа? (Чтобы найти часть числа, выраженную дробью, надо целое число разделить на знаменатель и умножить на числитель дроби)
- Прочитайте ответ задачи.
- А теперь преобразуем задачу. Что ещё мы можем найти в этой задаче? (Площадь незаштрихованной части)
- Как? (Из целого, то есть из площади нужно вычесть площадь заштрихованной части, а ещё можно через дробь)
- А какой из этих двух способов более рациональный, удобный?
- Что можно ещё найти? (Разницу между заштрихованной частью и незаштрихованной частью)
- Посмотрите, какие мы молодцы! Из одной задачи мы смогли составить и решить три задачи.
- А знание какого правила нам помогло? (Правило нахождения части числа)
- Как найти часть числа? (Чтобы найти часть числа, выраженную дробью, надо целое число разделить на знаменатель и умножить на числитель дроби)
8. Итог урока.
- Чему учились на уроке? Что нового узнали?
- Сколько нам пришлось размышлять, думать логически, выстраивать логические цепочки чтобы справиться с решением заданий. А это и есть те качества, которыми должен обладать логист и другой специалист.
xn--i1abbnckbmcl9fb.xn--p1ai
Седовская общеобразовательная школа
Математика
4 класс
Тема урока:
«Ознакомление с дробями»

Подготовила учитель начальных классов
Чекунаева Е.Г.
Тема. Ознакомление с дробями.
Цель: довести до сознания детей как образовываются дроби; показать запись дроби и ознакомить с терминами числитель и знаменатель; развивать логическое мышление, математическую речь, познавательную активность; воспитывать стремление достигать поставленную цель, чувство ответственности, уверенности в себе, умение работать в коллективе.
Тип урока: урок совершенствования знаний и умений
Оборудование: Наглядный материал, карточки, интерактивная доска,
презентация.
Ход урока
І Организационный моментСоздание ситуации успеха.Девиз урока:
Думать – коллективноРешать – оперативноОтвечать – доказательноРаботать – старательноИ это для всех обязательно.
Перед тем, как приступить к работе вспомним, какие правила мы должны соблюдать на уроке? (Учитель выслушивает ответы детей)
ПРАВИЛА:
Слушать.
Слышать друг друга.
Дополнять.
Исправлять, помогать.
ІІ Актуализация опорных знаний
-Вычислив значения выражений и расположив их в порядке возрастания, вы узнаете тему урока:
1. «Мозговой штурм» Устный счет
Р 6300 : 100 : 7 x 9 = 81
О 12000 : 4000 х 7 х 10 = 210
Б 720 : 90 x 10 x 8 = 640
И 90 x 30 : 100 x 1000= 27000
Д 16 x 100 : 10:40 = 4
2. Работа в тетрадях
-Записать число, классная работа, тема урока.
3. Минутка каллиграфии
-Напишите ту цифру, которая у вас меньше всего получается.
4 Технология «Микрофон»
У немцев сохранилась пословица: Попасть в дроби, то есть попасть в трудное положение. Я думаю, что сегодня мы выдержим все испытания и преодолеем все трудности.
О какой дроби пойдет речь? (охотничья дробь, барабанная дробь и обыкновенная дробь)
Какие цели и задачи стоят сегодня перед нами? (Наша задача выяснить- смогут ли дроби поставить нас в затруднительное положение или нет?
ІІІ Изучение нового материала
1.Практическая работа. Работа в парах
- У вас на столах фигуры. Возьмите прямоугольник. Разделите его на 2 части, не пользуясь линейкой и карандашом. (Ученики находят выход: разделить перегибанием.)
- На сколько частей разделили прямоугольник? (На 2 части)
- Заштрихуйте 1 часть.
- Сколько частей не раскрашено?
- Возьмите круг. Разделите его на 4 части, не пользуясь линейкой и карандашом. (Ученики действуют так же).
- Сколько получилось частей? (4 части)
- Закрасьте 1 часть. Какая это часть круга? (четвертая)
- Сколько частей не раскрашено? (3 части)
Дополнительно: Самая известная из долей – это, конечно. Половина. Слова с приставкой “пол” можно услышать часто: полчаса, полкилометра. Разделить целое на две равные части – половина. Долю называют “половина”. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на три части - “треть”. Долю называют “треть”. Если целое разделить на 4 равные части, то получится или по-другому говорят “четверть”. Скажите, когда мы говорим четверть? (Учебная четверть, четверть часа)
2. Объяснение материала учителем.
а)Нахождение долей
(арбуз разделили на 6 долей, 1 доля-…)
б)Вывод: в математике существуют числа, выражающие части единиц счета (измерения). Они называются – дроби.
(Число под чертой показывает на сколько равных частей разделен отрезок.
Число над чертой показывает, сколько таких частей взяли.
3. Игра "Числитель-знаменатель"
Чтобы запомнить, что такое числитель и знаменатель и не путать их поиграем в игру. Если я называю числитель, поднимаем руки вверх - показываем, что он записывается сверху. Если я называю знаменатель, показываем, что он пишется внизу. Если показываю черту дроби, складываем руки горизонтально
4.Игра «Доли»
Найти дробь и щелкнуть по ней мышкой, записать в тетрадь.
-Мы делили апельсин…
5. Работа в группах.
-Какая часть фигуры закрашена ?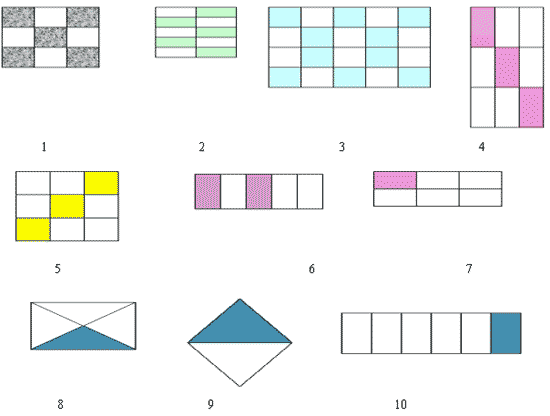
Записать.
6.Решить задачи (устно)
ІV Развитие математических умений учащихся
1.Комментированное решение задачи №662
2.Решение логической задачи
-Как разрезать головку сыра на 8 равных долей, сделав только 3 разреза?
V Рефлексия
Оцените свою работу на уроке. Если вам понравилось, то улыбнитесь, если было трудно и вы что-то не поняли, задайте вопрос.
Каждый из обучающихся произносит продолжение одной из фраз:
На уроке я узнал…
Мне было легко…
Я пока затрудняюсь…
Я узнал новое…
Я понял, мне необходимо поработать над темой.
VІ Домашнее задание
Решить задачи № 664, 665 на стр. 102, выучить правило стр. 101
VІ І Итог урока
- Что мы называем дробью?
- Как записывается дробь?
- Что обозначает дробная черта?
- Как называются числа дроби? Что показывает числитель? Знаменатель дроби?
Спасибо за внимание!
infourok.ru