Репетитор по математике о задачах на дроби в 5-6 классе. Как научить ребенка дробям 4 класс
Образование, чтение и запись дробей

Разделы: Начальная школа, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,5 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Предмет: математика.
Тип урока: урок обобщения и систематизации.
Тема: “Образование, чтение и запись дробей”.
Класс: 4
Цели:
- закрепить умение определять, на сколько равных
частей, долей разделена величина и сколько таких
частей взято;
- научить читать и записывать обыкновенные дроби;
- научить сравнивать дроби, опираясь во всех
случаях на рисунок;
- познакомить на наглядном примере с основным
свойством дроби;
- закрепить умение детей ориентироваться в
определении времени.
Конспект урока
I. Устный счёт.
- Объясните, как получить 1/2 долю круга?
Продемонстрируйте ответ.
- Круг разделили на 6 равных частей. Как назовете
одну такую часть? Продемонстрируйте, как
получить сложением одну шестую часть круга.
- Что означает выражение " 1/3 отрезка"?
- В 1/10 части початка кукурузы 93 зерна. Сколько
зёрен в целом початке?
- На свете существует 150 разновидностей акул, но
лишь 1/5 часть нападает на человека. Сколько видов
акул нападает на человека?
- Верблюд живёт 40 лет. 1/5 часть своей жизни он
растёт. Сколько лет растёт верблюд?
- В Древнем Риме соревнования проводились в
течение 1/3 года. Сколько месяцев в году длились
соревнования?
- 1/5 часть ленты составляет 10 метров. Какой длины
лента?
- Составьте свою задачу на нахождение числа по
доле. Каким действием она будет решаться?
Подберите фигуру вместо знака вопроса. (Слайд
2) Докажите.
(Круг разбит на 6 частей: 6Х3=18; круг разбит на 8
частей: 8Х4=32; круг разбит на 4 части: 4Х6=24)
II. Объяснение нового материала.
Введение в тему.
- Как называется этот предмет? (Слайд 3)
Где вы его встречали? На сколько одинаковых
частей разделён жезл? Покажите 1/5. (Дети
показывают 1/5 часть разными способами. Их
действия подкрепляются появлением надписей по
щелчку мыши).
- Покажите две одинаковые части. Как мы запишем,
что это 2 части из пяти? (По щелчку мыши появляется
надпись “2/5”)
- Что показывает эта запись?
- На этом слайде вы видите запись. (Слайд 4)
2 – это числитель, 5 – это знаменатель. Эта запись
показывает, что мы взяли 2 доли из 5. Такая запись
называется – дробь. (По щелчку мыши появляется
слово “дробь”)
- Прочитайте дробь.
- Возвращаемся к жезлу. (Слайд 5) Теперь
покажите мне три части из пяти. (По щелчку мыши
появляются разные способы решения данного
задания).
- Запишите дробь. Проверьте. (Слайд 6)
- Какая дробь, по вашему мнению, будет следующей?
(Слайды 7, 8)
- Если мы возьмём все 5 долей из пяти – то, что
получится? Это целое число.
- На слайде (Слайд 9) вы видите жука из
семейства усачей. Сравните, раскраску усов с
жезлом. Как вы думаете, почему такая раскраска у
жезла? Зачем этому жуку такие полосатые усы?
(Ответы детей)
Кульминационный фрагмент.
Отгадайте загадку:
Ранним утром ей не спится
Очень хочется трудиться
Вот и меду принесла
Работящая... (пчела)
- Как называется данный плод работы пчёл? (Слайд
10)
- Сколько ячеек сотов мы видим у пчелы? (15) (Слайд
11)
- Покажите 1/15 долю. (По щелчку мыши выделяется 1/15
доля по–разному).
- Две ячейки объединились. Какой дробью можем
обозначить результат? Как получили 2/15?
- Сколько ячеек сотов выделено цветом? Как
обозначим дробью 4 ячейки из 15?
Усложнение материала.
- Что произошло? (Слайд 12) (Из 15 ячеек
сотов исчезли 3).
- Сколько ячеек осталось? (12)
- Покажите 1/12 (Обратите внимание на знаменатель,
почему в знаменателе 12?).
Ещё 1/12 и ещё 1/12. (По щелчку мыши выделяются
цветом доли – появляется “столбик” из трёх сот)
- А теперь представьте себе, что это вовсе не
ячейки сотов, а ... (во время паузы ученики могут
пофантазировать, что это могут быть вазы, абажуры
настольных ламп и т.п.).
- Сколько ваз вы видите? Сколько оранжевых ваз?
Запишите, что оранжевая ваза у нас одна из
четырёх.
- Сравните. Раньше мы говорили, что это 3/12, а
теперь говорим, что это1/4. Сделайте вывод.
Подумайте, как у нас получилось такое равенство.
(Ученики могут сделать вывод, что если мы
числитель и знаменатель дроби 3/12 разделим на 3, то
получится 1/4)
4. Физкультминутка. (Слайд 13)
Пчёлка по лугу летела
И на кашку тихо села.
Посидела, посмотрела.
Потянулась к солнышку.
Улыбнулась, подбочась
За работу принялась.
Тренировочные упражнения.
Циферблат часов (Слайд 14) разделён на 2
части.
- Покажите 1/2.
- Разделим циферблат на 4 части (По щелчку мыши
проводится вертикальная черта). Покажите 1/4, 2/4.
Сравните 2/4 и 1/2. сделайте вывод. Покажите 3/4.
Разделим циферблат на 12 частей. (По щелчку мыши
циферблат делится на 12 частей)
- Покажите 1/12, 3/12. С какой дробью можно уровнять
3/12? (Можно вспомнить про “вазы”).
- Покажите на циферблате (Слайд 15) четверть
четвёртого; без четверти 7. (На макете часов дети,
передвигая стрелки, показывают указанное время)
- Найдите ответы и узнайте, что нарисовано: (Слайд
16)
2/5 от 15 – это...;
3/7 от 28 – это...;
2/9 от 72 – это....
- Решите задачу:
- В нашем классе 28 человек. 3/4 учатся на “4” и
“5” (хорошисты), а остальные отличники. Сколько
отличников в классе? Рассмотреть разные способы
решения с опорой на наглядность. (Слайды 17, 18 и
19).
III. Задания на развитие смекалки и
сообразительности.
Слайд 14.
- Раздели прямой линией циферблат часов на 2
части так, чтобы сумма чисел на обеих частях была
одинаковой.
(Подсказка: Сложить все числа, разделить сумму
на 2)
Слайд 15.
- Из семи палочек выложена дробь 1/7. Как,
передвинув одну палочку, получить дробь 1/3.
Слайд 16.
- Сколько перед вами квадратов? (14)
Удалите 3 палочки так, чтобы квадратов стало 4.
В этом задании можно вернуться к повторению.
Например, сколько одинаковых, маленьких
квадратов вы видите? Покажите 2/9, 4/9 и т.д.
IV. Подведение итога урока.
- Молодцы! Мы смогли справиться с очень трудной
темой. Но это только начало очень интересной
работы с дробями. Мы научились дроби
образовывать, читать, писать. А ещё нам предстоит
дроби сравнивать, складывать, умножать, делить и
вычитать, сокращать.
Дополнительная информация:
Слово “соты” при склонении может вызвать
затруднения. Привожу выдержку из толкового
словаря русского языка авторов: Ожегов С.И.,
Шведова Н.Ю.
СО/ТЫ, - ов, ед. сот, - а, м. У пчёл,
ос; симметрически расположенные ряды
шестигранных ячеек для хранения мёда и кладки
яиц. Рамка с сотами (в пчелином улье). Мёд в
сотах.II прил. сотовый, - ая, - ое. С. мёд
(находящийся в сотах)
Литература:
- Труднев В.П. Внеклассная работа по математике в
начальной школе. Пособие для учителей. М.:
“Просвещение”, 1975
- Арутюнян Е.Б., Левитас Г.Г. Занимательная
математика. – М.: АСТ-ПРЕСС, 1999
xn--i1abbnckbmcl9fb.xn--p1ai
Понятие дроби для 4- 5 класса, изучаем наглядно дроби от 5 лет
Дата: 13 марта 2014
Автор: Алина
Рубрика: Правила

Когда же в школе проходят дроби?… Класс 4-й, кажется, или чуть раньше. Сложная тема, ничего не скажешь. Но вот интересно: жизнь знакомит ребёнка с дробями гораздо раньше школьной программы! Первый раз это происходит, когда хочется поделиться с другом конфетой, а она всего одна. И вот ребёнок уже знает, что такое «половина» и что значит «пополам». А юные музыканты, придя в первый класс музыкальной школы, сталкиваются с дробями буквально на первом уроке: целые ноты, половинные, четвертные, «восьмушки». И на примере яблока малышам объясняют, что это такое. Стало быть, можно начинать первое знакомство с дробями пораньше. Почему бы и нет? Если это будет наглядно, доступно, просто, то ребёнок усвоит эту премудрость легко и играючи.
«Дробная» математика для детей
Договоримся сразу, что дробь — это часть целого, меньше единицы. На сколько частей мы будем делить целое? А это как договоримся. Что будем считать единицей? Тоже как договоримся. Вот такие они сговорчивые, эти дроби. И ещё нужно запомнить одну вещь: то число, на сколько частей мы решили делить целое — это знаменатель, сколько этих частей мы взяли — это числитель.
Например, вот такая история. На траве лежат 3 яблока, ёжик взял только 2. За целое (единицу) мы возьмём все яблоки — весь урожай. Но их у нас 3, значит, наш урожай делится на 3 части. 3 — это знаменатель. Весь урожай (единица) — это 3/3, а каждое яблоко — это 1/3 урожая. Раз ёжик взял 2 яблока, значит, он взял 2/3 урожая!
А можно взять лего, такой любимый многими детьми конструктор. Мы ведь давно заметили, что все его элементы разные по размеру, правда? И на каждой детальке разное количество точек-«пупырышек». Посчитаем — вот одна, две, четыре, шесть и даже восемь.
Давайте за целое (единицу) будем считать «кирпичик» лего с восьмью точками. Для начала сравним его с другими. Сколько деталек лего с 4-мя точками нужно взять, чтобы получился наш «кирпичик»-единица? Правильно, две. Значит, одна деталька с 4-мя точками — это 1/2 нашей «единицы». А сколько деталек с двумя точками нужно взять, чтобы получить целое? Верно, четыре. Стало быть, одна такая деталька — это 1/4. А деталь с одной точкой -это 1/8, потому что таких деталек понадобится аж 8 штук, чтобы получилось целое. Теперь задачка посложнее: перед нами элемент с шестью точками. В нём помещается 3 «четвертинки», а если добавить к нему ещё одну — получится целое (единица). Итак, вот и первый пример готов: 3/4+1/4=4/4 или же 1 (если числитель и знаменатель равны, значит, это единица!)
Это далеко не единственный эксперимент, который можно провести с лего. С дробями-то можно договориться о многом. А что, если мы то же самое, будем считать не четвертями, а восьмыми? И знаменателем у нас будет 8? Смотрим на картинку: единица — «кирпичик» с восьмью точками. 1/2 — это получается 4/8, а 1/4=2/8. А это уже история о том, как можно сокращать дроби. Но эта тема, действительно, может немножко подождать!Автор: Юлия Белка
(Visited 11 309 time, 1 visit today)
Оцените статью: Поделитесь с друзьями!
Метки:
shkolabuduschego.ru
Как научиться решать дроби? - Полезная информация для всех
Сама столкнулась с тем, что дроби оказались достаточно сложной темой для моих детей.
Есть очень хорошая игра quot;Дроби Никитинаquot;, она предназначена для дошкольников, но и в школе отлично поможет ребенку разобраться , что же все-таки это такое - дроби, их соотношение друг к другу..., причем все в доступной, наглядной и увлекательной форме.
Представляет она из себя двенадцать разноцветных кругов. Один круг - целый, а все остальные поделены на равные части - две, три.... ( до двенадцати).
Ребнку предлагается выполнить несложные игровые задания, например:
Как называютсячасти кружков? или
Какая часть больше? ( наложить меньшую на большую.)
Моим эта методика помогла. Вообще очень жалею , что все эти quot; Никитинские развивашкиquot; не попались на глаза, когда дети были еще малышами.
Игру можно сделать самостоятельно или купить готовую, а узнать обо всем подробней - здесь.
Решение дробей можно объяснить и на кубиках Lego. Он развивает не только воображение, но и творческое и логическое мышление, а значит, его можно использовать и как учебное пособие.
Алишия Зиммерман придумала использовать кубики известного конструктора для обучения детей основам математики.
И вот как на основе конструктора Lego можно объяснить дроби.
Практика показывает, что больше всего трудностей возникает при сложении (вычитании) дробей с разными знаменателями и при делении дробей.
Трудности возникают из-за кривых указаний в учебнике, как, например, разделить дробь на дробь.
quot;Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а числитель второй дроби на знаменатель первой дробиquot;.
Может ли ребенок в 4 классе это понять и не запутаться? НЕТ!
А нам учительница объяснила элементарно: нужно вторую дробь перевернуть, а потом умножить!
Тоже самое со сложением.
quot;Чтобы сложить две дроби, нужно числитель первой дроби умножить на знаменатель второй дроби, а числитель второй дроби умножить на знаменатель первой дроби, полученные числа сложить и записать в числитель. А в знаменатель нужно записать произведение знаменателей дробей. После этого полученную дробь можно (или нужно) сократитьquot;.
А проще так: quot;Приведите дроби к общему знаменателю, который равен НОК знаменателей, а потом сложите числителиquot;.
Показать им на наглядном примере. Например, яблоко разрежьте на 4 части, на 8, на 12 сложите в целое, сложите несколько частей, отнимите. При этом на бумаге объясняйте с использованием правил. Правила сложения, вычитания. деления дробей, а так же как из неправильной дроби выделить целое - вс это учите в ходе манипуляций с яблоком. Не торопите детей, пусть внимательно с вашей помощью разберутся с дольками.
Научить решать дроби, в частности детей, это дело вполне обычно и не создаст много хлопот. Самое просто что можно сделать, это взять что-то целое, например мандарин, или любой другой плод, разделить его не части, и на примере показывать вычитания, сложение и другие операции с кусочками этого плода, что и будет дробями от целого. Все нужно объяснять и показывать, и завершающим фактором будет на математических примерах объяснять и решать задания совместно, пока ребенок сам не научиться делать эти задания.
На рисунке наглядно видно что чему соответствует и как смотрится дробь на реальном предмете, именно так и нужно объяснять.
Вам к этому вопросу, нужно подойти основательно, так как решение дробей в жизни пригодится. Нужно в этом вопросе, как говорится, с детьми быть на равных, и объяснять теорию на им доступном языке, например на языке quot;тортаquot; или мандарина. Нужно делить торт на до и раздавать друзьям, после чего ребенок начнет вникать в суть решения дробей. Не начинайте с тяжелых дробей, начните с понятий 1/2, 1/3, 1/10. Сначала отнимайте и прибавляйте, а потом переходите на более сложные понятия как умножение и деление.
Проблемы с дробями бывают разные. Один ребнок не может понять, что одна вторая и пять десятых - это одно и то же, у других вызывает недоумение приведение различных дробей к одному знаменателю, у третьих - деление дробей. Поэтому и одного правила на все случаи жизни нет.
Главное в задачах на дроби - не упустить момент, когда понятное перестат таковым быть. Возвращаться к quot;печкеquot; и повторять вс сначала, даже если оно кажется убого-примитивным. Например, вернуться к тому, что такое одна вторая.
Ребнок должен понять, что математические понятия - абстрактны, что одно и то же явление можно описать разными словами, выразить разными числами.
Мне нравится ответ, данный Mefody66. Добавлю из личной многолетней практики: научить решать задачи с дробями (а не решать дроби; решать дроби нельзя, равно как невозможно решать числа) довольно несложно, надо лишь быть рядом с ребенком, когда он только приступает к решению таких задач, вовремя корректировать его решение, дабы ошибки, которые неизбежны при любом обучении, не успели закрепиться в сознании ребенка. Переучивать сложнее, чем учить новое. И как можно больше решать таких задач. Довести до автоматизма решение таких заданий - вот это хорошо бы сделать. Умение решать задачи с обыкновенными дробями по важности в школьном курсе математики занимает такое же место, как и знание таблицы умножения. Так что надо не полениться и проследить, как ваш ребенок решает такие задачи.
И не очень опирайтесь при этом на учебник: учителя в школах объясняют именно так, как писал в своем ответе Mefody66. Лучше поговорить с учителем, выяснить, какими словами учитель объяснял эту тему. И использовать по возможности те же слова и фразы (чтобы не сильно запутывать ребенка)
Еще: наглядные примеры использовать советую лишь на начальном этапе объяснения, потом побыстрее абстрагироваться, переходить к алгоритму решения. Иначе наглядность может повредить при решении более сложных задач. Например, если надо сложить дроби со знаменателями 29 и 121 - какая тут наглядность поможет? Только запутает.
Дроби - одна из тех благодатных математических тем, где нет не приложимых к делу абстракций. В ход идти должны продукты ( на quot;тортахquot; , как Хуаните Солис в quot;Отчаянных домохозяйкахquot; - реально классный метод объяснений). Все эти числители-знаменатели - потом. Потом нужно, чтобы ребенок понял, что деление на дробь уже и не уменьшение вовсе, а умножение- не прибавка. Тут лучше показать, как делить на дробь в форме умножения на перевертыш. В игровой форме подать сокращение, если делятся на одно число, то делить, почти судоку получается, если заинтересовать. Главное вовремя заметить непонятки, потому что дальше будут темы покруче, которые понять не просто. Поэтому побольше практики решении дробей и все быстро наладится. Мне, гуманитарию наичистейшему, далкому от малейшей степени абстракции, дроби всегда были понятны, чем остальные темы.
info-4all.ru
Как объяснить ребенку в 3-4 классе дроби? С чего нужно начать?
Математика… Бесконечные цифры, числа, слагаемые, вычитаемые, равно, разделить, умножить. И со всем этим предстоит столкнуться вашему ребенку, ну а вам освежить в памяти и объяснить, если на уроке не все было понятно. С целыми числами все понятно: вот апельсин, а вот еще один. Но как наглядно объяснить школьнику, что такое дроби? Наша статья подскажет, что нужно сделать, чтобы ваш маленький математик смог со всем разобраться.
Как показать и объяснить ребенку дроби
Представить в уме, что такое, например, две трети ребенку сложно, поэтому дробь нужно показать. Для демонстрации понадобятся следующие подручные средства:
- Мелки для рисования на асфальте.
- Конфеты, пряники, леденцы либо другие сладости, которые можно показывать по одной.
- Фрукт, состоящий из долек (апельсин, грейпфрут и т. д.).
- Яблоко.
- Специальный обучающий круг, состоящий из секторов.
Как использовать данные предметы:
- Предложите ребенку на улице сыграть в классики. Как известно, в процессе игры обучение проходит легче, а результаты получаются более продуктивными. Начертите стандартные классики с клетками и цифрами: 1, 2, 3 и т. д. Пусть малыш проскачет их все, называя вслух цифры. А теперь в нескольких секторах разделите клетку пополам и объясните, что к предыдущей теперь будет добавлена половина. То есть вместе цифры 4 сначала идет 3,5, а уже потом целая четверка, ведь клетка состоит из половин.
- Выложите перед школьником две конфеты. Предложите разделить их поровну между ним и вами. Скорее всего, это не вызовет затруднений. Теперь усложните задачу: достаньте еще всего лишь одну конфету. Что же делать теперь? Вполне возможно, ваше чадо скажет, что поделить на двоих одну конфету невозможно. Докажите ему обратное, разрезав сладость пополам. Объясните, что целое можно поделить на две составные части, и называться это будет одна вторая.
- Неполные числа хорошо демонстрировать на цитрусовых дольках. Возьмите, к примеру, мандарин. Сначала разделите его пополам. Расскажите ребенку, как получилось такое деление, и как оно называется. Каждую половину разделите еще раз поровну. И так до тех пор, пока вы не получите отдельные дольки. Такой наглядный пример поможет ребенку в будущем представлять дроби в уме.
Вместо фрукта можно использовать обучающий круг с секторами.
- Если нет фрукта с дольками, возьмите обычное яблоко. Предложите малышу угостить друга, но так, чтобы лакомство досталось им обоим. Если он не сможет сам понять, как это сделать, объясните ему все так же, как на примере апельсина (мандарина, грейпфрута и т. д.), отрезая от яблока дольки соответствующего размера.
Объяснить дроби ребенку – занятие, требующее терпения и правильной формулировки. Не ругайте ученика, если он не сразу сможет осознать информацию, которую до него пытаются донести. Ваш позитивный настрой и вера в его силы способны на многое, в конце концов, у вас все получится.
o-kroha.com
Дроби
Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы возьмёте себя в руки и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?
Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово дробь тоже говорит за себя — дробь означает дробление, деление, разделение.
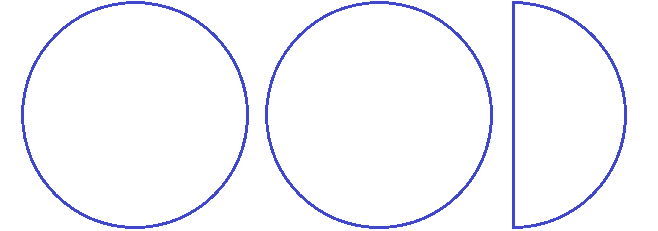
Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим, мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.
 Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
 Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
 А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
 Такие записи называют дробями. Дробь состоит из числителя и знаменателя.
Такие записи называют дробями. Дробь состоит из числителя и знаменателя.
Число, которое записывается сверху называется числителем дроби.
Число, которое записывается снизу называется знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая»
или так: «один кусок из четырёх»,
или так: «одна четвёртая доля»,
или так: «четверть».
Всё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь? Очень просто. Сверху записываем 2 (поскольку мы уже съели два куска), а внизу записываем 4 (поскольку всего кусков было 4):
 В этой дроби числитель это 2, а знаменатель это 4. Эта дробь читается так: «две четвёртых» или так: «два куска из четырёх».
В этой дроби числитель это 2, а знаменатель это 4. Эта дробь читается так: «две четвёртых» или так: «два куска из четырёх».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три. Допустим мы съели один кусок этой пиццы. Как записать такую дробь? Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается 3, поскольку пицца разделена на три части, а сверху этой линии записывается 1, поскольку съеден один кусок:
Допустим мы съели один кусок этой пиццы. Как записать такую дробь? Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается 3, поскольку пицца разделена на три части, а сверху этой линии записывается 1, поскольку съеден один кусок:
 В этой дроби числитель это единица, а знаменатель — тройка. Эта дробь читается так: «Одна третья»
В этой дроби числитель это единица, а знаменатель — тройка. Эта дробь читается так: «Одна третья»
или так: «Один кусок из трёх»,
или так: «Одна третья доля»,
или так: «Треть».
Если мы съедим два куска этой пиццы, то такая дробь будет называться «две третьих» и записываться вот так:

Теперь представьте, что пиццу мы разделили на две части или как говорят в народе «пополам»:
 Допустим из этих двух кусков мы съели один кусок. Как записать такую дробь? Очень просто. Опять же рисуем линию. Внизу этой линии записываем 2, поскольку пицца разделена на две части, а вверху записываем 1, поскольку съеден один кусок:
Допустим из этих двух кусков мы съели один кусок. Как записать такую дробь? Очень просто. Опять же рисуем линию. Внизу этой линии записываем 2, поскольку пицца разделена на две части, а вверху записываем 1, поскольку съеден один кусок:
 Эта дробь читается так: «одна вторая»,
Эта дробь читается так: «одна вторая»,
или так: «один кусок из двух»,
или так: «одна вторая доля»,
или так: «половина».
Дроби, которые мы рассмотрели выше, называют обыкновенными. Почему обыкновенными? Потому что дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Десятичные будем рассматривать немного позже. Обыкновенная дробь эта та дробь, которая состоит из числителя и знаменателя.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На рисунке показаны знаменатели для каждой разделенной поровну пицце:
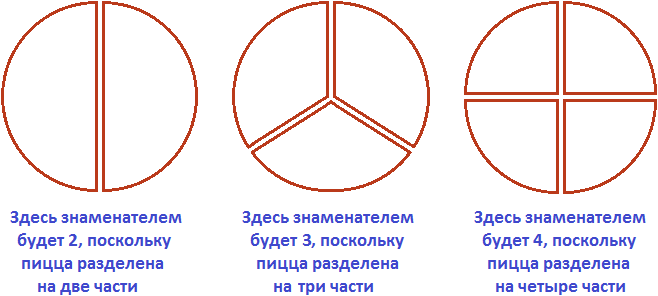
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли  (одну часть из двух) или как говорят в народе «половину» пиццы.
(одну часть из двух) или как говорят в народе «половину» пиццы.
С помощью переменных дробь можно записать так:
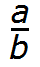 где a — это числитель, b — знаменатель.
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильные и неправильные.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
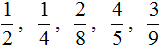
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём  (одну четвёртую пиццы), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
(одну четвёртую пиццы), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
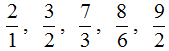 Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько это «чего-либо» разделено. А числитель показывает сколько этого «чего-либо» взяли.
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько это «чего-либо» разделено. А числитель показывает сколько этого «чего-либо» взяли.
Теперь возьмём к примеру неправильную дробь 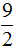 и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
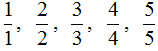
Вообще, такие дроби даже не имеют права называться дробями. И вот почему. Рассмотрим к примеру дробь 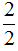 . Применим её к нашей пицце.
. Применим её к нашей пицце.
Допустим, мы хотим съесть 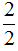 пиццы. В знаменателе стоит 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По-сути, взята вся целая пицца, и если мы съедим эту
пиццы. В знаменателе стоит 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По-сути, взята вся целая пицца, и если мы съедим эту 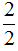 пиццы, то съедим не часть пиццы, а всю пиццу целиком. Другими словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
пиццы, то съедим не часть пиццы, а всю пиццу целиком. Другими словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь 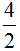 . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
. Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
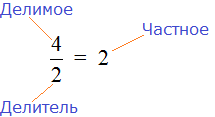
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
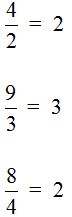
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного посложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части в дроби».
Выделение целой части в дроби
Вычислим дробь 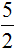 . Пять разделить на два будет два и один в остатке:
. Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
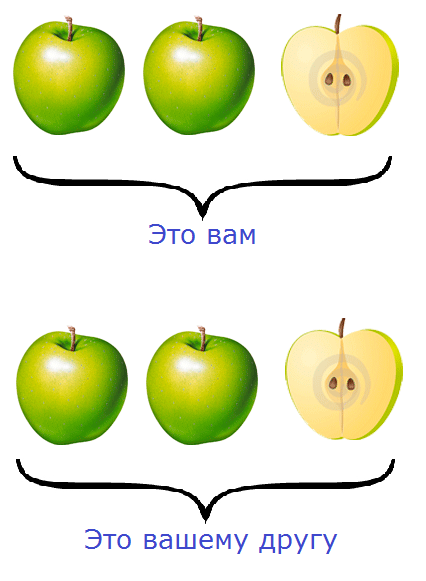
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби 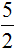 и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
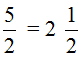
Схематически это выглядит так:
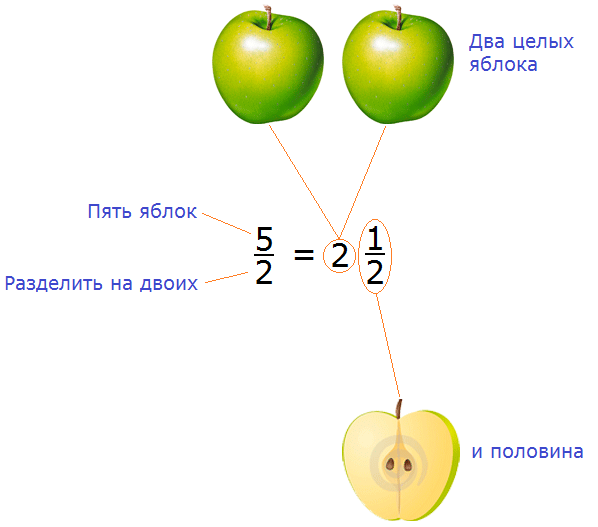
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.
В нашем примере мы выделили целую часть у дроби  и получили новую дробь
и получили новую дробь 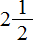 . Такую дробь называют смешанной. Смешанная дробь это дробь у которой есть целая часть и дробная.
. Такую дробь называют смешанной. Смешанная дробь это дробь у которой есть целая часть и дробная.
В нашем примере целая часть это 2, а дробная часть это 
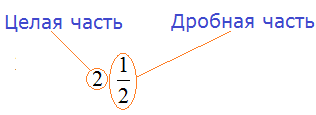
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:
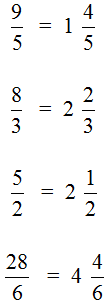
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби 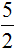 . Записываем уголком данное выражение и решаем:
. Записываем уголком данное выражение и решаем:
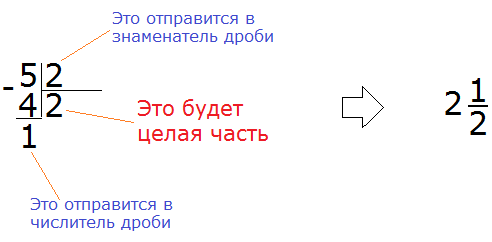
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Главное понять, что куда отнести. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть в дроби 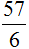
Записываем уголком данное выражение и решаем. Далее собираем смешанную дробь:

Получили: 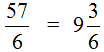
Перевод смешанного числа в неправильную дробь
Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь 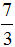 . Если выделить в ней целую часть, то получается
. Если выделить в ней целую часть, то получается 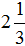
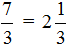
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель остаётся прежним.
Например, переведём смешанное число 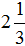 в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем к 6 прибавляем числитель дробной части:
6 + 1 = 7
Полученная семёрка будет числителем новой дроби, а знаменатель останется прежним:

Подробное решение выглядит так:

А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
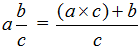
Пример 2. Перевести смешанное число 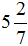 в неправильную дробь.
в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем прежним: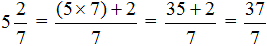
Основное свойство дроби
Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Что это значит? Это значит, что значение дроби не изменится.
Например, рассмотрим дробь  . Умножим её числитель и знаменатель на одно и то же число, например на число 2:
. Умножим её числитель и знаменатель на одно и то же число, например на число 2:
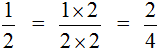
Получили новую дробь  . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби  и
и  равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь  (один кусок из двух), а второй иллюстрирует дробь
(один кусок из двух), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и оттуда взяли один кусок. А вторая пицца была разделана на четыре куска, и оттуда взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и оттуда взяли один кусок. А вторая пицца была разделана на четыре куска, и оттуда взяли два куска.
Поэтому, между дробями  и
и  можно поставить знак равенства (=) потому что эти дроби несут одно и то же значение. Другими словами, они равны:
можно поставить знак равенства (=) потому что эти дроби несут одно и то же значение. Другими словами, они равны:
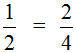
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь 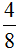 . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2:
. Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2:
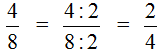
Получили новую дробь  . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби 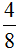 и
и  равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь 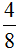 (четыре куска из восьми), а второй иллюстрирует дробь
(четыре куска из восьми), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и оттуда взяли четыре куска. А вторая пицца была разделана на четыре куска, и оттуда взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и оттуда взяли четыре куска. А вторая пицца была разделана на четыре куска, и оттуда взяли два куска.
Поэтому, между дробями 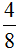 и
и  можно поставить знак равенства (=) потому что эти дроби несут одно и то же значение. Другими словами, они равны:
можно поставить знак равенства (=) потому что эти дроби несут одно и то же значение. Другими словами, они равны:
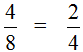
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Сокращение дробей
Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь  выглядит намного проще и красивее, чем дробь
выглядит намного проще и красивее, чем дробь 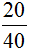 .
.
Если при решении задач и примеров получается большая некрасивая дробь, то нужно пытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на общий делитель называется сокращением дроби.
Пример 1. Сократим дробь 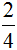 . Надо разделить числитель и знаменатель на наибольший общий делитель чисел 2 и 4.
. Надо разделить числитель и знаменатель на наибольший общий делитель чисел 2 и 4.
В данном случае, дробь простая и для неё НОД ищется легко. НОД { 2 и 4 } это 2. Значит числитель и знаменатель дроби 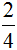 надо разделить на двойку. Итак, делим числитель и знаменатель на 2:
надо разделить на двойку. Итак, делим числитель и знаменатель на 2:
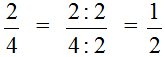
Пример 2. Сократим дробь 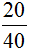 . Чтобы сократить эту дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40. НОД { 20 и 40 } это 20. Значит делим числитель и знаменатель дроби на 20:
. Чтобы сократить эту дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40. НОД { 20 и 40 } это 20. Значит делим числитель и знаменатель дроби на 20:
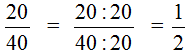
Пример 3. Сократим дробь 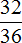 . Чтобы сократить эту дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36. НОД { 32 и 36 } это 4. Значит делим числитель и знаменатель дроби на 4:
. Чтобы сократить эту дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36. НОД { 32 и 36 } это 4. Значит делим числитель и знаменатель дроби на 4:
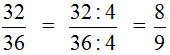
Если в числителе и знаменателе стоят простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.
Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть данного способа заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби 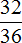 . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
. Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
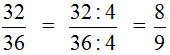
Теперь представьте, что в данном выражении отсутствует конструкция 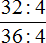 , и сразу записан ответ
, и сразу записан ответ  . Получится следующее выражение:
. Получится следующее выражение:
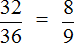
Суть в том, что число на которое разделили числитель и знаменатель хранят в уме. В нашем случае, числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записывают рядом с числителем, предварительно зачеркнув его:
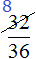
Затем, точно так же делят знаменатель на число 4. Полученный ответ записывают рядом со знаменателем, предварительно зачеркнув его:
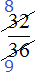
Затем собирают новую дробь. В числитель отправляют новое число 8 вместо 32, а в знаменатель отправляют новое число 9 вместо 36
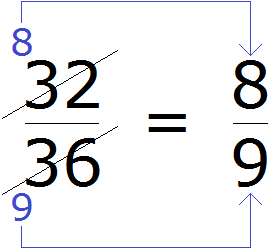
Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Также дроби можно сокращать, предварительно разложив на множители числитель и знаменатель. Например, сократим дробь 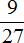 предварительно разложив на множители числитель и знаменатель:
предварительно разложив на множители числитель и знаменатель:
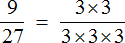
Итак, мы разложили числитель и знаменатель дроби 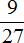 на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение: 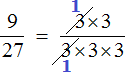
Сократить можно ещё по тройке в числителе и в знаменателе:
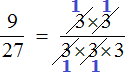
Далее сокращать больше нечего. Последнюю тройку в знаменателе просто так сократить нельзя, т.к. в числителе нет множителя, который можно было бы сократить вместе с ней.
Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
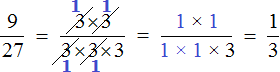
Получили ответ  . Значит при сокращении дроби
. Значит при сокращении дроби 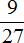 получается новая дробь
получается новая дробь  .
.
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на множители числителя и знаменателя, если вы только начинаете изучать математику. Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решен старым способом и будет выглядеть так:
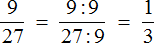
Сравните это выражение, с выражением которое мы получили, когда пользовались вторым способом
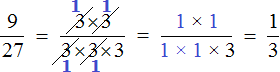
Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?
Задания для самостоятельного решения
Задание 1. Запишите в виде дроби следующий рисунок:

Задание 2. Запишите в виде дроби следующий рисунок:
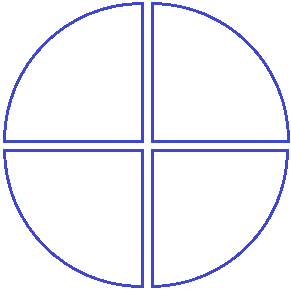

Задание 3. Запишите в виде дроби следующий рисунок:
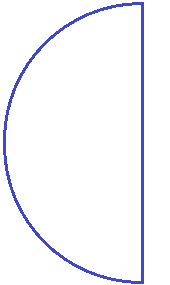

Задание 4. Запишите в виде дроби следующий рисунок:
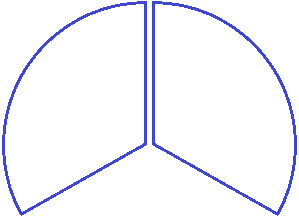
Задание 5. Запишите в виде дроби следующий рисунок:


Задание 6. Выделите целые части в следующих дробях:
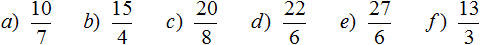
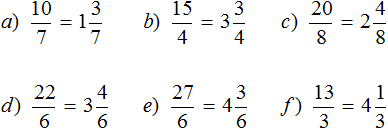
Задание 7. Выделите целые части в следующих дробях:
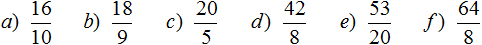
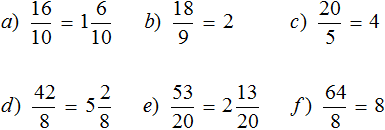
Задание 8. Переведите смешанные дроби в неправильные:
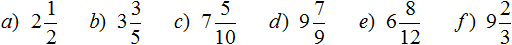
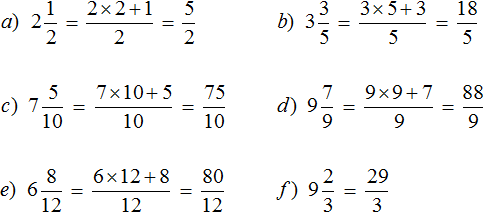
Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части
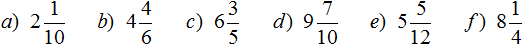
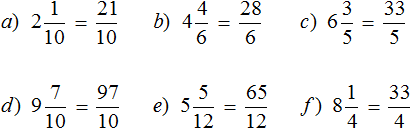
Задание 10. Сократите следующую дробь на 3

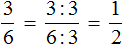
Задание 11. Сократите следующую дробь на 3 вторым способом

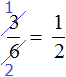
Задание 12. Сократите следующую дробь на 5
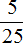
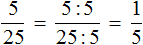
Задание 13. Сократите следующую дробь на 5 вторым способом
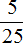

Задание 14. Сократите следующие дроби:
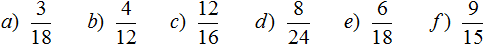

Задание 15. Сократите следующие дроби вторым способом:
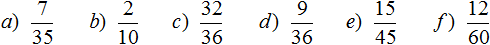
Задание 16. Запишите в виде дроби следующий рисунок:
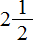
Задание 17. Запишите в виде дроби следующий рисунок:

Задание 19. Запишите в виде дроби следующий рисунок:

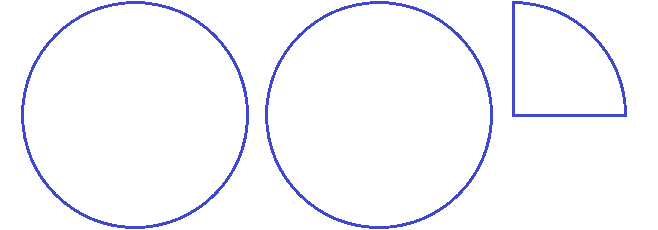
Задание 20. Запишите в виде дроби следующий рисунок:


Задание 21. Запишите в виде дроби следующий рисунок:

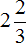
Задание 22. Изобразите в виде рисунка следующую дробь:

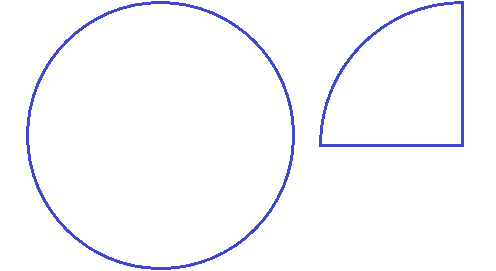
Задание 23. Изобразите в виде рисунка следующую дробь:
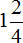
Задание 24. Изобразите в виде рисунка следующую дробь:
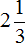
Задание 25. Изобразите в виде рисунка следующую дробь:
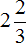

Задание 26. Изобразите в виде рисунка следующую дробь:
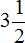
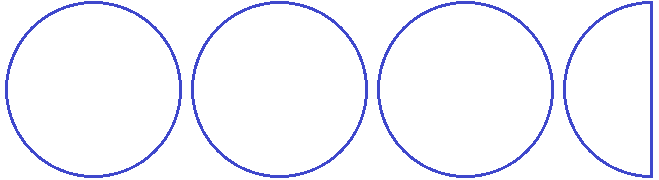
Задание 27. Изобразите в виде рисунка следующую дробь:

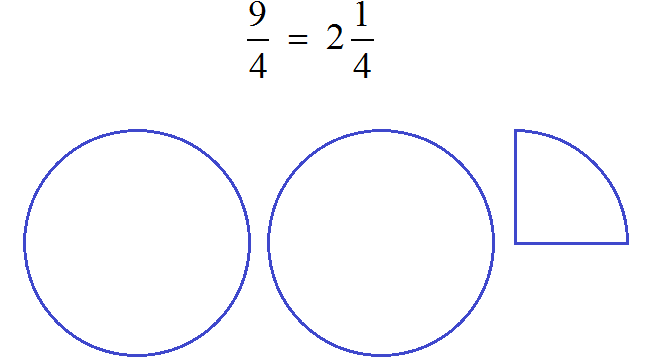
Задание 28. Изобразите в виде рисунка следующую дробь:


Задание 29. Изобразите в виде рисунка следующую дробь:

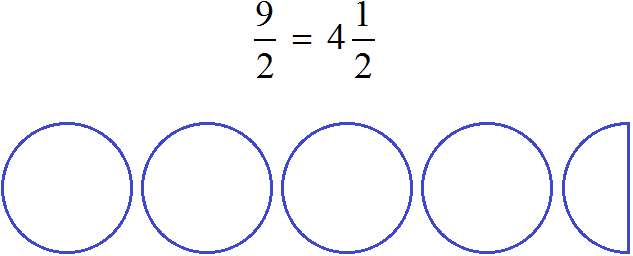
Задание 30. Изобразите в виде рисунка следующую дробь:

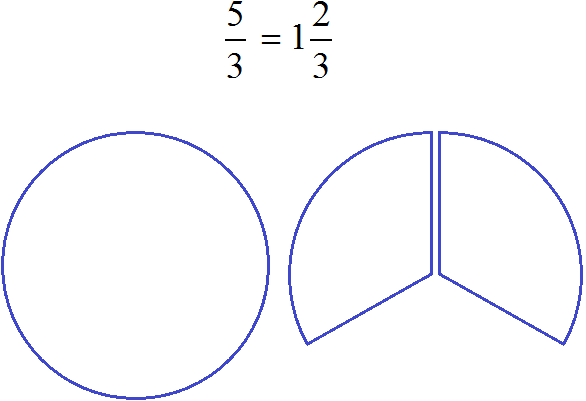
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
10 математических подсказок, которые научат вас считать очень быстро • Фактрум
Умножение? Проценты? Дроби? Да запросто! С математическими лайфхаками от Фактрума всё это больше не будет представлять для вас проблемы. А детишкам-школьникам наша шпаргалка пригодится ещё больше! Поделиться
Класснуть
Мы предлагаем вашему вниманию десять картинок, после внимательного изучения которых страшное слово «математика» больше не будет пугать даже самого «безнадёжного гуманитария»!
Запоминаем знаки «больше» и «меньше»
 Источник иллюстраций: You-journal.ru
Источник иллюстраций: You-journal.ruТаблица умножения на 9 — легкотня!

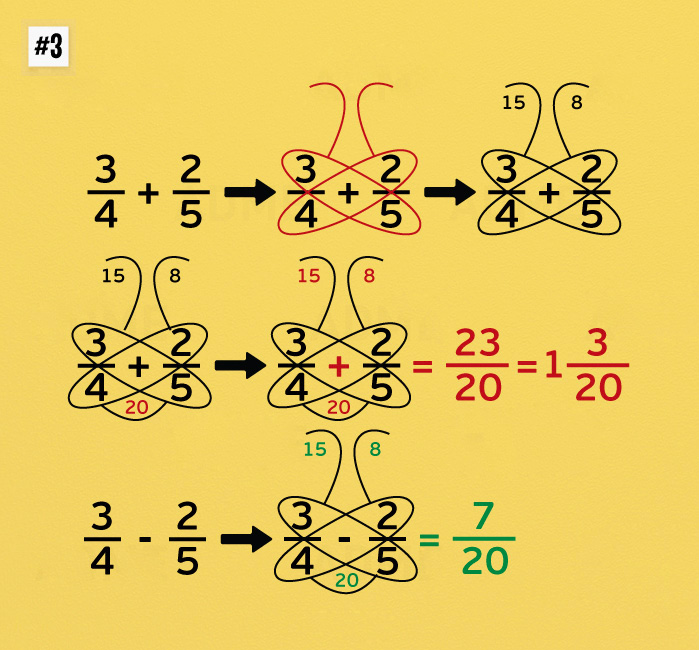
Используйте «метод бабочки» для действий с дробями
На 11 умножать ещё приятнее
Немного лирики с числом Пи

Не вспомнить, а посчитать
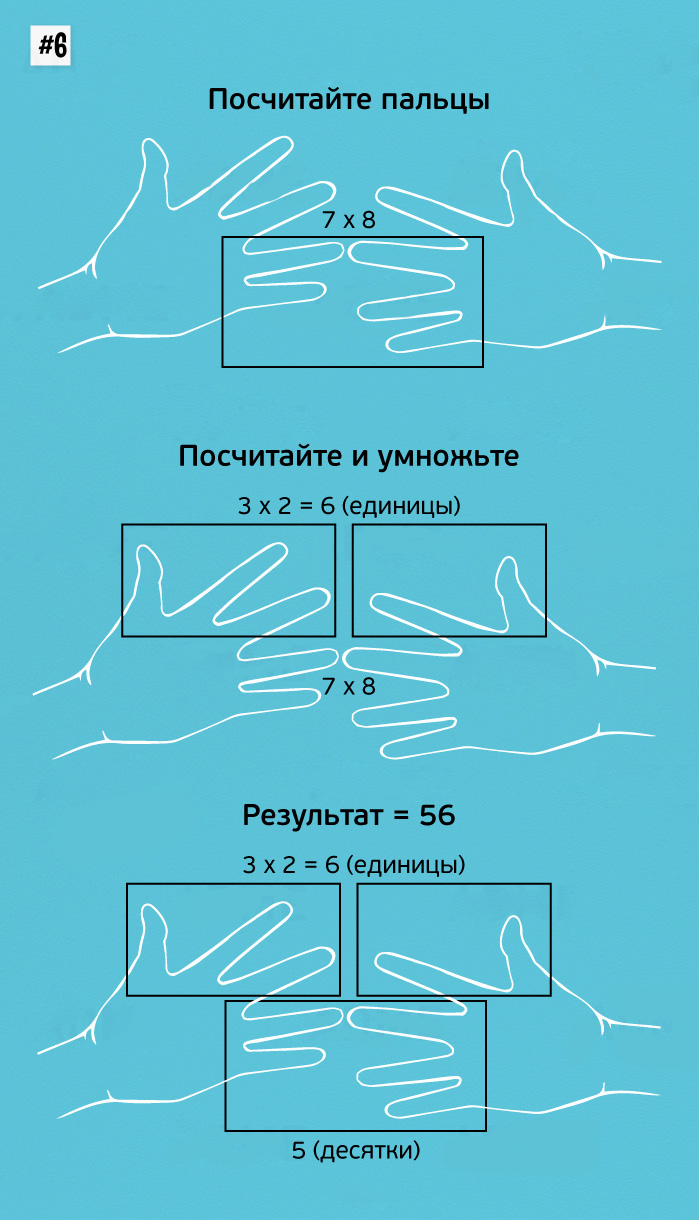
Теперь научимся комфортно перемножать двузначные числа
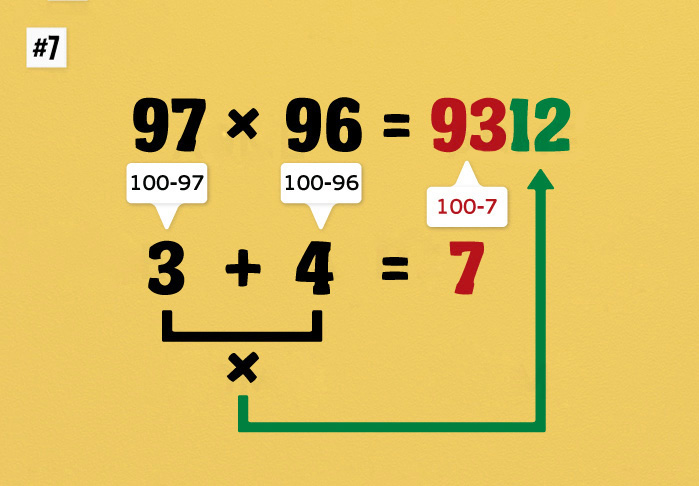
Считать налоги или наценку — запросто!

Переходим к делению — гениальный трюк!

А это пригодится в кулинарии!

Читайте также: 10 обалденных фактов о математике, которые понравятся даже гуманитариям
Понравился пост? Поддержи Фактрум, нажми: Поделиться
Класснуть
www.factroom.ru
Репетитор по математике о задачах на дроби в 5-6 классе
Задачи на части (на дроби) в 5 — 6 классе, безусловно, тяжелейшая тема для преподавания. Возможно даже самая тяжелая за весь школьный курс. Как может построить свою работу с ней репетитор по математике? Рассмотрим некоторые приемы обучения решению таких задач, опишем связанные с темой проблемы и поговорим о ее дидактике.
Причиной большинства обращений к репетитору в 5 классе является повальное непонимание законов разделения на части. Это естественно, ибо задачи, на которых формируется представление о долях, предъявляют достаточно высокие (для этого возраста) требования к уровню развития ученика, часто связанные с его физиологией. Этот обстоятельство часто не позволяет репетитору математики действовать стандартно, опираясь на традиционые объяснения.
Несмотря на влияние физиогогии родители ребенка обычно стараются повлиять на ситуацию как можно быстрее. Большинству из них нужен репетитор по математике для скорейшего исправления текущей отметки. Иногда это мешает планомерно и неспешно объяснять математические законы и выстраивать темы в логически правильном порядке.
Долгое время я не решался написать об этих задачах. И дело не только в сложности восприятия материала школьниками. В изучении темы выделяется несколько этапов с различными ограничениями в использовании чисел. Не случайно дроби проходят не один год. Программа 5 класса переплетается с программой 6-го класса (а по Петерсону еще и с четвертым). Поэтому даже при одном и том же характере работы преподавателя с дробями разница в индивидуальных особенностях учеников и программах не позволяют описать методы работы репетитора по математике с темой точно и коротко. Более того, в разных учебниках «доли» изучаются в разное время, по-разному «обкладываются» задачами и по-разному интегрируются в дидактику смежных тем. Поэтому очень сложно охватить все проблемы. Надеюсь, что репетиторы по математике со стажем меня понимают.
Много раз я сталкивался с проблемами задач на дроби и уяснил для себя главное: тема требуют постепенного и долгого изучения. Ее нельзя проработать за один-два урока. Поэтому первое, что я делаю, — объясняю родителям ситуацию и прошу предоставить дополнительные часы для занятий. Не менее двух раз в неделю. Для репетитора по математике это стандартный график, позволяющий в большинстве случаев полноценно заниматься пробелами.
Репетитор по математике о своей методике
Формально мой подход не отличается от того, что предлагают другие репетиторы, а именно — решение задач в большом количестве. Однако к ним еще нужно поготовить ученика, предложить ему некий план или даже алгоритм подбора пути решения. К сожалению, его точность и прозрачность не всегда соответствует желаемому. Репетитор по математике должен понимать, какие задачи и с каким учеником следует разбирать, в каком порядке и в каком количестве. Подходы разных преподавателей могут отличаться порядком разбора задач, пояснениями, терминологией, сопровождениями в рисунках, схемах и даже их полным отсутствием. Я использую собственную базу типовых примеров и наводящих вопросов, систему записей, оформлений и обозначений (немного схожую с Петерсоновской). Оптимизирую краткие записи к задачам, делаю их удобными, информативными и ориентированными на поиск решения.
Попробую изложить ...
Разбор элементарных задач
Первый этап работы репетитора — знакомство ученика с базовыми задачами, обучение составлению для них кратких записей. Очень важно вложить в ученика мысль о том, что сложная задача на дроби состоит из нескольких упакованных в нее простых, с определенной последовательных элементарных операций. Их выделением и проработкой репетитор по математике занимается на первом уроке.
Выделяется 3 типа простейших задач на дроби:1) Целая величина известна2) Целая величина неизвестна3) Неизвестна дробь
Для каждой из них подбирается реальная ситуация, которую удобно моделировать рисунком. Распространены примеры деления яблока или плошади. Например: Яблоко имеет массу 160 грамм, найдите вес  яблока. Пример стандартный, но подходит не всех ученикам, ибо для проверки правильности демонстрируемых репетитором ариметических действий приходится делить то, что нельзя взять в руки, именно вес. При низком интеллектуальном уровене развития ученика репетитор по математике оказывается бессильным что-либо ему объяснить, ибо проблемы уходят далеко от темы «дроби». Если такое происходит, я использую пример с полом:
яблока. Пример стандартный, но подходит не всех ученикам, ибо для проверки правильности демонстрируемых репетитором ариметических действий приходится делить то, что нельзя взять в руки, именно вес. При низком интеллектуальном уровене развития ученика репетитор по математике оказывается бессильным что-либо ему объяснить, ибо проблемы уходят далеко от темы «дроби». Если такое происходит, я использую пример с полом:
Пол выложен одинаковыми плитками как показано на рисунке. На каждую плитку положили по шарику. Сколько шариков лежит на  пола?
пола? 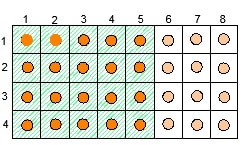 Преимущество этого примера в том, что ребенок может не только выделить (закрасить) 5/8 пола, но и пересчитать количество шариков непосредственно. При этом репетитор по математике указывает на возможность ответить на вопрос через простые арифметические действия (на рядах и колонках).
Преимущество этого примера в том, что ребенок может не только выделить (закрасить) 5/8 пола, но и пересчитать количество шариков непосредственно. При этом репетитор по математике указывает на возможность ответить на вопрос через простые арифметические действия (на рядах и колонках).
Наводящие вопросы репетитора по математике
Cлабого ребенку можно еще и полдвести к выполнению действий. Для этого репетитор по математике задает ему систему наводящих вопросов, например:
Репетитор: сколько колонок на рисунке?Ученик: 8 колонокРепетитор: сколько шариков расположено в одной колонке?Ученик: 4 шарикаРепетитор: Каким действием это можно найти?Ученик: 32:8=4Репетитор: сколько колонок в 5/8 пола?Ученик: 5 колонокРептитор: Если в одной колонке 32:8=4 шарика, то в пяти колонках шаров будет ...Ученик: 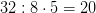 шариков.Привильно !!!!!
шариков.Привильно !!!!!
Главное преимущество задачи на плитки и шарики состоит в использовании арифметических действий, каждое из которых удается проверить простым пересчетом. После того, как репетитор по математике убедился в понимании действий, он диктует ученику проверенное правило: «делим на знаменатель и умножаем на числитель».
Несмотря на то, что можно пересчитывать количество не шариков, а самих плиток, я намеренно оставляю шары в сюжете задачи. Почему? На их примере изучается ситуация, когда какой-нибудь целый объект удерживает внутри себя (или на себе) мелкие объекты (в нашем случае пол удерживает шарики). Это широко распространено в дидактике математики 5-6 класса. Часто что-то куда-то засыпается, заливается, вкладывается и равномерно распределяется по объекту. В мешки засыпают сахар, в бидоны заливают молоко и т.д. Репетитор по математике на примере шариков помогает ребенку быстрее разобраться в числовых особеннностях этих ситуаций и понять законы измерения частей объектов.
Далее ... На том же рисунке с шариками нужно поставить обратную задачу: Допустим, мы знаем, что на 5/8 пола лежит 20 шаров. Как найти их общее количество? И здесь репетитору по математике тоже помогает рисунок, на котором можно просто пересчитать кружочки. Легко подбирать и комментировать выполняемые действия: 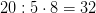 . Все ясно и прозрачно. Наводящие вопросы (если они нужны) аналогичны первому случаю.
. Все ясно и прозрачно. Наводящие вопросы (если они нужны) аналогичны первому случаю.
Репетитору по математике важно остановиться на терминологии и оформлении краткой записи.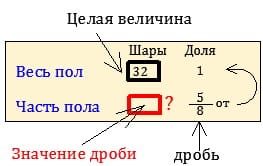 От того, насколько как она будет зависит идентификация правил. Ученик должен усвоить, что целый объект — это такая же величина, как и его часть, измеряемая двумя единицами: привычной (метрами, сантиметрами, килограммами, литрами, страницами, деревьями, шариками и т.д.) и «особой». В роли последней выступает целая величина. Рядом с ней в кратких записях можно поставить 1ед. Все участники элементарной задачи получают названия. То, от чего ищется часть называется целой величиной, сама дробь так и остается дробью, а часть, которую находят от целого репетитор по математике называет «частью» или «значением» дроби». Я предпочитаю второй вариант.
От того, насколько как она будет зависит идентификация правил. Ученик должен усвоить, что целый объект — это такая же величина, как и его часть, измеряемая двумя единицами: привычной (метрами, сантиметрами, килограммами, литрами, страницами, деревьями, шариками и т.д.) и «особой». В роли последней выступает целая величина. Рядом с ней в кратких записях можно поставить 1ед. Все участники элементарной задачи получают названия. То, от чего ищется часть называется целой величиной, сама дробь так и остается дробью, а часть, которую находят от целого репетитор по математике называет «частью» или «значением» дроби». Я предпочитаю второй вариант.
Как правило, к репетитору обращаются в момент, когда тема набрала обороты и в классе решают в перемешку задачи на разные базовые правила. Поэтому, их приходится включать в один урок. Если ребенок не самый слабый, то вместо плиток я применяю яблоко, причем с одним и тем же набором значений величин для всех типов задач. Выписываю из образцы в отведенную для этого теоретическую тетрадь (или на форзац рабочей тетради). Каждую запись отдельно комментирую и специальным образом оформляю:  Задача 1-го типа: целая величина известна.
Задача 1-го типа: целая величина известна.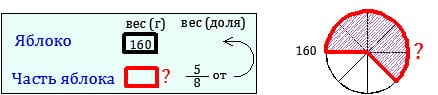
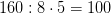 (г) -вес части яблока.Чтобы найти значение дроби нужно целую величину разделить на знаменатель и умножить на числитель.
(г) -вес части яблока.Чтобы найти значение дроби нужно целую величину разделить на знаменатель и умножить на числитель.
Задача 2-го типа: целая величина неизвестна.
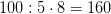 (г) — вес яблока.Чтобы найти целую величину нужно значение дроби разделеить на числитель и умножить на знаменатель.
(г) — вес яблока.Чтобы найти целую величину нужно значение дроби разделеить на числитель и умножить на знаменатель.
Задача 3-го типа: неизвестна дробь.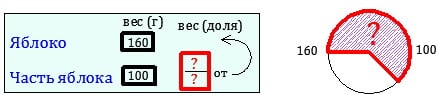
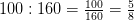 (яблока) -вес его части
(яблока) -вес его части
В третьей задаче для 5 класса репетитором по математике должны быть выбраны другие числа, ибо сократить дробь 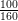 пятиклашки еще не могут. Обратите внимание на то, что обыгрывается один и тот же комплект чисел. В первой задаче репетитор по математике находит
пятиклашки еще не могут. Обратите внимание на то, что обыгрывается один и тот же комплект чисел. В первой задаче репетитор по математике находит 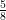 целого яблока, а во второй выполняет обратные действия: по той же дроби
целого яблока, а во второй выполняет обратные действия: по той же дроби 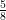 и найденному ранее значению 100 восстановливает число 160 (его даже можно в определенный помент стереть ластиком). Прием обратных действий полезен для работы с невнимательными школьниками. Он позволяет быстро сконцентрироваться на правилах, а не на изучении нового условия новой задачи. Более того, при заранее изветном ответе ребенок убеждается в правильности выбора этих действий. Действительно, как можно в них усомниться, если репетитор по математике получает в ответе то, что и должно получиться?
и найденному ранее значению 100 восстановливает число 160 (его даже можно в определенный помент стереть ластиком). Прием обратных действий полезен для работы с невнимательными школьниками. Он позволяет быстро сконцентрироваться на правилах, а не на изучении нового условия новой задачи. Более того, при заранее изветном ответе ребенок убеждается в правильности выбора этих действий. Действительно, как можно в них усомниться, если репетитор по математике получает в ответе то, что и должно получиться?
Под каждой краткой записью оформляется решение и записывается правило:
1) чтобы найти значение дроби, нужно целую величину разделить на знаменатель и умножить на числитель.2) Чтобы найти целую величну нужно разделить на числитель и умножить на знаменатель.3) Чтобы найти дробь нужно разделить ее значение на целую величину.
Как репетитор математики работает с комбинированными задачами
Чаще всего они встречаются в 6 классе, хотя в учебнике Петерсона сочетания двух и даже трех типов задач предлагаются уже в 5 классе. Прежде всего ученик должен знать с чего начинать исследование задачи. Важно отработать каждый его этап в отдельности.
Краткая запись
Краткая запись к задаче — важнейший и незаменимый элемент методики любого хорошего репетитора по математике. Она является одновременно и опорой и средством заставить ученика перечитывать условие как минимум — два три раза. Правильно составленная краткая запись в сочетании с четкими правилами «трех типов» позволяют разложить комбинированную задачу на несколько элементарных. Поэтому репетитору чрезвычайно важно научить правильно ее составлять.
Как репетитор по математике работает с текстами?Главной проблемой составления краткой записи является проблема анализа текста задачи. Практика показывает, что дети крайне невнимательно и низкоэффективно с ним работают. Не умеют выделять ценную информацию о величинах и сами величины, сортировать главное и второстепенное. Для борьбы с такими проблемами репетитор математики может взять на вооружение метод слежения. Что такое краткая запись? — всего лишь короткий текст условия, из которого выброшены лишние слова, а названия величин и их значения записаны отдельными строками. Что мешает репетитору по математике выделять эти слова в тексте? Особенно важно научить поиску целых величин, на которые в краткой записи будут указывать стрелки. Репетитор должен обратить внимание ученика на то, что слово или фраза, написанная сразу после дроби, указывает на единицу измерения дроби, то есть на ее целую величину. Репетитору по математике никто не запрещает выделить ее в тексте (подчеркнуть или записать другим цветом) и поставить к ней стрелочку. Пример оформления:
Если внимание ребенка ослаблено, на первых порах ему лучше предлагать уже размеченные тексты, с выделенными целыми величинами и стрелочками.
Для того, чтобы не пропустить ни одну из участвующих величин репетитору по математике нужно задать вопрос: Что в задаче можно измерить? Пок ученик думато, репетитор подчеркивает в тексте соответствующие им слова. В нашем случае это показано синим цветом.
Важно отработать поиск и применение типовых задач внутри комбинированной. Дети часто путают когда им делить на знаменатель, а когда на числитель. В 6 классе путают умножать ли на дробь или делить на нее. Проблема усугубляется когда в задачу встревает еще и сумма (разность) величин. Ребенок пытается запомнить эти ситуации, но от их многообразия пухнет голова. Чем может помочь ему репетитор по математике? Самое эффективное запоминание — зрительное. При многократном зрительрном анализе ребенок «фотографирует» расположение известных и неизвестных компонент выделенных репетитором строк (связанных «дробной стрелкой») и распознает эту же комбинацию величин в другой задаче. по нему в другой задаче что именно надо лелать. Для увеличения числа обращений к правилам типовых задач я рекоментдую репетиторам по математике использовать визуальные образы задач (без текстов). Репетитор подает ученику задачу ее краткой записью с полной информацией о всех известных взаимосвязях между величинами . Сложности возникают с суммами нескольких величин. В таком случае репетитору по математике приходится искать дополнительные обозначения для суммы. Я решил это пробьлему так: поле суммы закрашивается, а поля ее слагаемых обводятся тем же цветом по периметру. Очень удобно. Если какое-то из слагаемых тоже равно сумме других, более мелких величин, то его внутренняя частсь закрашивается другим цветом, а поля слагаемых этим же цветом обводятся по контуру. И таких вложений может быть сколько угодно.
Например, краткая запись к задаче про вишню может быть следующей:
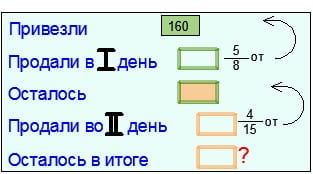
Попрбуйте составить краткую запись к олимпиадной задачке: мама испекла булочки. Аня съеха 2/3 всех булочек и еще 2. Петр съел 2/3 остатка и еще 2 булочки, а Денис съел 2/3 последнего остатки и последние 2 булочки. Сколько булочек испекла мама?
Александр Николаевич, репетитор по математике Москва (м.Щукинская, Строгино)
Метки: Работа репетитора, Репетиторам по математике
ankolpakov.ru