Основное свойство пропорцииСвойствоПроизведение крайних членов пропорции равно произведению ее средних членов.
Обратное свойствоСвойство Пример
Производные пропорцииПравило Пример
Правило ! По трем известным членам пропорции всегда можно найтиее неизвестный член. Пример
ОтношенияОпределение Отношением двух чисел a и b называется их частное a : b. Показывает во сколько раз a больше b или какую часть число a составляет от b.1 Примеры отношенийПример 1 Отношение числа 16 к числу 4 равно 16 : 4 = 4, т.е. 16 в 4 раза больше чем,чем 4. Пример 2 Отношение числа 4 к числу 12 равно 4 : 12 = 13, т.е. 4 составляет третьот числа 12. Пример 3 Масса стакана с жидкостью равна 440г. Стакан весит 40г. Какую часть всей массы составляет масса стакана? Во сколько раз масса стакана с жидкостью больше массы жидкости?Решение: Масса стакана составляет 40 : 440 = 1 11 часть полной массы. Масса жидкости равна 440 - 40 = 400г; масса стакана с жидкостью больше массы самой жидкости в 440 : 400 = 1,1 раза.
пропорции в 6 классе | математика-повторениеЗадача 1. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги? Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги: 3,3:300 или х:500. Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений): 3,3:300=х:500. Неизвестный средний член пропорции равен произведению крайних членов пропорции, деленному на известный средний член. (Подробно о пропорции и нахождению ее крайнего, среднего членов читайте в статье: «6.1.1. Пропорция. Основное свойство пропорции.») х=(3,3·500):300; х=5,5. Ответ: пачка 500 листов бумаги имеет толщину 5,5 см. Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде: или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см. Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6 классе. Задача 2. Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды? Решение. Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы. 5:100 или х:98. Получаем пропорцию: 5:100 = х:98. х=(5·98):100; х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды. Задача 3. Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти? Решение. Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти: 16,8:21 или х:35. Получаем пропорцию: 16,8:21=х:35. Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35) и делим на известный средний член (21). Сократим дробь на 7. Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5 (5 и 10) и на 3 (168 и 3). Ответ: 35 литров нефти имеют массу 28 кг. Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля? Решение. Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это: х:100 или 9:18. Составляем пропорцию: х:100 = 9:18. Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9) и делим на известный крайний член (18). Сокращаем дробь. Ответ: площадь всего поля 50 га. www.mathematics-repetition.com Что такое пропорция | МатематикаЗдесь мы рассмотрим, что такое пропорция, как называются члены пропорции и основное свойство пропорции. Определение пропорции: Пропорция — это равенство двух отношений. С помощью букв пропорцию записывают так:
или
Читают: «a относится к b как c относится к d» или «отношение a к b равно отношению c к d». Числа a и d называют крайними членами пропорции, числа b и c — средними членами пропорции: Примеры пропорций: 1) 4,8:1,6=3,6:1,2 Здесь 4,8 и 1,2 — крайние члены пропорции, 1,6 и 3,6 — средние члены пропорции.
Здесь 2,1 и 6 — крайние члены пропорция, 8,4 и 1,5 — средние члены пропорции. Основное свойство пропорции: Произведение крайних членов пропорции равно произведению ее средних членов.
Отсюда следует, что
Таким образом, если в пропорции поменять местами крайние члены или средние члены, то получим новые верные пропорции. Пропорция- это равенство. Если это равенство содержит переменную, значение которой надо найти, то оно является уравнением. Как решать пропорции, мы рассмотрим в следующий раз.Кроме того, пропорции используются для решения некоторых задач. В частности, пропорции существенно облегчают решение задач на проценты. Позже мы рассмотрим также решение задач с помощью пропорций. www.for6cl.uznateshe.ru
www.yaklass.ru Пропорция. Основное свойство пропорции - 6 классГоловач Александр Григорьевич ГУО «Средняя школа №18 г. Бреста» Тема: Пропорция. Основное свойство пропорции. (6 класс) Тип урока: изучения и первичного закрепления новых знаний Образовательная: познакомить учащихся с понятиями: пропорция и члены пропорции; научить чтению пропорции и составлению пропорций из отношений; познакомить учащихся с основным свойством пропорции и сформировать навык по определению верной пропорции. Развивающая: активизировать познавательную деятельность учащихся; развивать память, логическое мышление; Воспитательная: воспитывать уважение к труду, работе в коллективе. Литература: Математика: учеб. пособие для 6 кл. общеобразоват. учреждений с рус. яз. обучения / Е. П. Кузнецова [и др.]; под ред. Л. Б. Шнепермана. – Минск: Нац. ин-т образования, 2010. — 320 с.: ил. Оборудование: учебник, доска, мел, презентация, компьютер, проектор. Ход урока:
1. Организационный момент Организую внимание учащихся. Предлагаю сесть. Отмечаю отсутствующих на уроке учеников. Здороваются. Садятся. 2. Проверка домашнего задания - Сегодня у нас на уроке новая тема «Пропорция. Основное свойство пропорции». И цели нашего урока: познакомиться с определение «Пропорция»; из каких элементов состоит пропорция; изучить основное свойство пропорций. Но перед тем, как приступить к изучению новой темы, давайте проверим домашнее задание. 3. Актуализация знаний /*фронтальный опрос*/ - На прошлом уроке у нас была тема «Отношение чисел и величин». 1. Давайте вспомним, что же называется отношением? 2. А как называются сами эти числа или величины? 3. Скажите, что будет с отношением, если его члены умножить или разделить на одно и тоже число, отличное от нуля? А теперь давайте вспомним, как читаются отношения и найдем их значение. 1. 2. 3. 4. 5. 6. 1. Частное двух чисел (или двух величин) называется отношением. 2. Эти числа или величины называются членами отношения. 3. Отношение не изменится, если его члены умножить или разделить на одно и тоже число, не равное нулю. 1. Отношение числа 25 к 5 равно 5. 2. Отношение числа 33 к 11 равно 3. 3. Отношение числа 6 к 14 равно . 4. Отношение числа 12 к 4 равно 3. 5. Отношение числа 30 к 70 равно 6. Отношение числа 55 к 11 равно 5. 4. Изучение нового материала - Ребята скажите, под какими номерами у наших отношений получились одинаковые значения. У нас получились записи равных отношений:
- Так вот равенство двух отношений называют пропорцией. Пропорцию записывают:
или Прочитать такую пропорцию можно по-разному: - отношение a к b равно отношению c к d; - a относится в b, как c относится к d; - a, деленное на b, равно c, деленное на d. Т.к. в записи числа a и d стоят с краю, то их принято называть крайними членами пропорции. Ну а т.к. числа b и c находятся в середине, то и называются они соответствующе – средними членами пропорции. Эти названия сохраняются и тогда, когда пропорция записана в виде . Давайте вернемся к получившимся у нас пропорциям и назовем их крайние и средние члены.
А теперь немного посчитаем. Перемножьте в наших пропорциях крайние и средние члены
Какой вывод можно сделать? , то Верно. Это утверждение называется основным свойством пропорции. Отношение 1 равно отношению 6. Отношение 2 равно отношению 4. Отношение 3 равно отношению 5. Крайние 25 и 11, средние 5 и 55. Крайние 33 и 4, средние 11 и 12. Крайние 6 и 70, средние 14 и 30.
Произведение крайних членов пропорции равно произведению ее средних членов. 5. Физкультминутка - Ну а теперь немного отдохнем. Проведем физкультминутку для глаз. Т.к. уже зима, то на экране будут появляться снежинки, а ваша задача внимательно следить за их движениями. 6. Первичное закрепление - А теперь с новыми силами начнем выполнение заданий. № 5.27 (устно) 5.29 (1;3) 5.30 (1;3) 5.31 (1;3) (доп. 5.32) № 5.27 1) ; 2) ; 3) ; 4) . №5.29 (1;3) Составьте пропорцию, если m и n – ее крайние члены, а x и y – средние: 1) ; 3) ; № 5,30 (1;3) Определите, является ли пропорцией равенство. 1) 3) № 5,31 (1;3) 1) 3) № 5.27 1) 5,1 относится к 3, как 34 относится к 20. Крайние члены: 5,1 и 20. Средние члены: 3 и 34. 2) 4,4 относится к 0,66, как 10 относится к 1,5. Крайние члены: 4,4 и 1,5. Средние члены: 0,66 и 10. 3) 4 относится к 25, как 16 относится к 100. Крайние члены: 4 и 100. Средние члены: 25 и 16. 1) 6 относится к 31, как 18 относится к 93. Крайние члены: 6 и 93. Средние члены: 31 и 18. №5.29
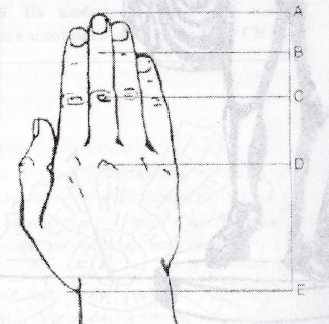
1) или 3) или № 5,30 (1;3) 1) нет 3) нет № 5,31 (1;3) 1) да 3) да 7. Задание на дом - Откройте дневники и запишите задание на дом: п.5.2 №5.29-5.31 (2;4) 8. Рефлексия. Подведение итого Подведение итогов. 1. С каким новым определение Вы сегодня познакомились? 2. Что такое «Пропорция»? 3. Какие члены пропорции бывают? 4. Как звучит основное свойство пропорции? Выставляю отметки за урок. Рефлексия. Предлагаю учащимся продолжить фразу: “Сегодня на уроке я узнал…”, “Было интересно…”, “Было трудно…”, “Меня удивило…”, “Я хотел бы узнать…”, “Сегодня на уроке я научился…”. Ответы: 1. С определением «Пропорция». 2. Пропорция – это равенство двух отношений. 3. У пропорции бывают крайние и средние члены. 4. Произведение крайних членов пропорции равно произведению ее средних членов. infourok.ru конспект урока "Отношения и пропорции" 6 классВоронцова Галина Николаевна Муниципальное казенное общеобразовательное учреждение «Старокармыжская средняя общеобразовательная школа» Конспект урока по математике 6 класс «Отношения и пропорции» Цель: - сформировать понятие пропорции, отношения. - закрепить новые понятия. - совершенствовать навык счета. - развивать чувство гармонии, прекрасного. Оборудование: - плакат с опорным конспектом. - наглядность (рисунки) - бумага, ножницы, линейка Тип урока: изучение нового материала Ход урока. 1.Изучение нового материала. (можно использовать слайды по определениям и задачам, записи отношений и пропорций) Примеры на доске: 7:2 1:8 Учитель: Прочесть записи на доске. Ученики: частное чисел 7 и 2; 1 и 8; четыре седьмых; пять третьих; отношение чисел 4 и 7; отношение чисел 5 и 3 Учитель: вы употребили новое понятие «отношение», некоторым из вас оно может уже знакомо, некоторые его встретили при чтении энциклопедии и других источников по математике. Давайте мы поподробнее ознакомимся с этим понятием. Определение: Отношением чисел называют частное двух чисел не равных 0, Отношение показывает, во сколько раз первое число больше второго или какую часть первое число составляет от второго. По словарю Ожегова - Отношение 1. Взаимная связь разных величин, предметов, действий. 2.Частное, получаемое от деления одного числа на другое, а также запись соответствующего действия (запись понятия на отдельном листочке и вывешивается на доске). Если значения двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин (отношением длин, отношением масс и т.д.) Частное двух величин называют отношением величин. Учитель: Запишем дату, тему урока «Отношения и пропорции» и определение отношения в тетради. 2.Закрепление понятия «отношение. 1). «Г» (говори правильно) – стр. 121, №706 – отношения читает каждый ученик про себя, затем один вслух. 2).№ 706 (стр. 121), используя слово «отношение» прочитайте записи и назовите члены отношений. 3) творческое задание учащимся: составить всем по одному отношению и назвать их по очереди. Учитель: Как же обстояло дело с понятием « отношение» раньше? 3. Историческая справка. При решении разнообразных практических задач часто приходится сравнивать однородные величины между собой, вычислять их отношения. Долгое время под числом понималось только натуральное число (собрание единиц), полученное в результате счета. Отношение как результат деления одного числа на другое не считалось числом. Новое определение числа было дано впервые английским ученым Исааком Ньютоном(1643-1727). В своей «Всеобщей арифметике» он писал: «Под числом мы понимаем не столько множество единиц, сколько отвлеченное отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу». Вот с тех пор и считается что отношение величин одного наименования есть число. 4. Продолжение изучения нового материала. Учитель: Рассмотрим следующие пары отношений 20:4 и 1/3:1/15 6:3и18:9 1,2:4 и 3:10 (запись на доске) -Что можно сказать про эти отношения? (проблемный вопрос для класса). Ученики: если найти отношения, то получатся одинаковые ответы в правой и левой частях и можно между ними поставить знак равно. Учитель: пары отношений равны между собой. Определение. Равенство двух отношений называется пропорцией. В буквенном виде пропорция записывается следующим образом а : в = с : д или а, д – крайние члены; с, д – средние члены. Правильное чтение пропорций (отношений, записанных выше). По словарю Ожегова: Пропорция - 1)Равенство двух отношений 2)Определенное соотношение частей между собой, соразмерность(в частях здания). Для запоминания определения пропорции можно выучить следующее четверостишие: Кто с задачами постарается Тот не упустит решений. А пропорцией называется Равенство двух отношений. 5.Историческая справка про «пропорции». В древности учение о пропорциях было в большом почете у пифагорийцев. С пропорциями они связывали мысли о порядке и красоте в природе, о созвучных аккордах в музыке и гармонии во вселенной. В 7 книге «Начал» Евклида (3 в. до н.э.) изложена теория отношений и пропорций. Современная запись пропорции выглядит так: а : в = с :д или в : а = д : с (а + в) : в = (с + д) :д а : (а – в) = с : (с – д ) а : с = в : д (а – в) : в = (с – д) :д Известный нам способ записи пропорций появился не сразу. Ещё в 17в. французский ученый Р.Декарт (1596-1650) записывал пропорцию 7 : 12 = 84 : 144 так /7/12/84/144/ Современная запись пропорции с помощью знаков деления и равенства была введена немецким ученым Г. Лейбницем (1646 – 1716) в 1693г. Вначале рассматривали только пропорции, составленные из натуральных чисел. В 4 в. до н.э. древнегреческий математик Евдокс дал определение пропорции, составленной из величин любой природы. Древнегреческие математики с помощью пропорций 1) решали задачи, которые в настоящее время решают с помощью уравнений, 2) выполняли алгебраические преобразования, переходя от одной пропорции к другой. Часть математики, в которой говорится об отношениях и пропорциях греки называли музыкой. Почему такое странное название? Дело в том, что греки создали и научную теорию музыки. Они знали: чем длиннее натянутая струна, тем ниже «толще» получается звук, который она издает. Они знали, что короткая струна издает высокий звук. Но у всякого музыкального инструмента не одна, а несколько струн. Для того чтобы все струны при игре звучали «согласно», приятно для уха, длины звучащих частей их должны быть в определенном отношении. Поэтому учение об отношениях, о дробях и стало называться музыкой. Пропорциональность является непременным условием правильного и красивого изображения предмета. Это мы видим в произведениях искусства, архитектуре, встречается в природе. Рисунки о пропорциональности в природе и искусстве, архитектуре. Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета. Творческое задание учащимся. Вырежьте из бумаги прямоугольник со сторонами 10 см и 16см. Отрежьте от него квадрат со стороной 10см. Что произойдет с прямоугольником, т.е. с отношением сторон? Затем снова от этого прямоугольника отрежьте квадрат со стороной 6см. Что произойдет в этом случае со сторонами прямоугольника? Ученики: в первом и во втором случаях остается прямоугольник, одна сторона которого примерно в 1,6 раза больше другого. Учитель: этот процесс можно продолжать и дальше. На прямоугольники, в которых стороны соотносятся приблизительно как 1,6:1, обратили внимание очень давно. Посмотрите на изображение храма Парфенон в Афинах (Приложение 1). Даже сейчас это одно из самых красивых сооружений мира. Этот храм построен в эпоху расцвета древнегреческой математики. И его красота основана на строгих математических законах. Если мы опишем около фасада Парфенона прямоугольник (Приложение 2), то окажется, что длина его больше ширины примерно в 1,6 раза. Такой прямоугольник назвали золотым прямоугольником. Говорят, что его стороны образуют золотое сечение. Понятие «золотого сечения» Золотое сечение или божественное деление – это такое деление целого на две неравные части, при котором большая часть относится к целому, как меньшая к большей. Число 1,6 лишь приближенно ( с точностью до 0,1) представляет величину золотого сечения. Пример 1.Если отрезок разделен на две части так, что меньшая имеет длину Х, а большая – длину У, то в случае золотого сечения У: (Х+У)=Х:У.
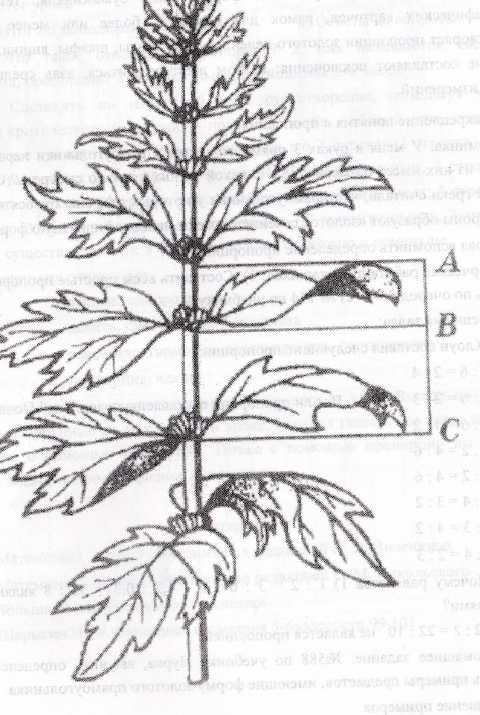
У Х Пример2. В правильной пятиконечной звезде каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения. С АС : (АС+СВ) = СВ : АСА В Пример 3. На изображении раковины точка С делит отрезок АВ приблизительно в золотом сечении. АС : СВ = СВ : АВ Пример 4. Знаменитая скульптура Аполлона Бельведерского. Если высоту великолепно сложенной фигуры разделить в крайнем и среднем отношении, то линия раздела окажется на высоте талии. Особенно хорошо удовлетворяет этой пропорции мужская фигура. Пример 5. Каждую отдельно взятую часть тела( голову, руку, кисть) также можно разделить на естественные части по закону золотого сечения. Пример 6. Расположение листьев на общем стебле растений. Между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В). Вывод: Можно привести множество подобных примеров. Нам кажутся одинаково некрасивыми и квадратная, и слишком удлиненная прямоугольная форма: и та, и другая грубо нарушают пропорцию золотого сечения. То же можно наблюдать и во многих других случаях, когда прямоугольная форма предмета не зависит от практических целей и может свободно подчиняться требованиям вкуса. Прямоугольная форма книг, бумажников, тетрадей, фотографических карточек, рамок для картин – более или менее точно удовлетворяет пропорции золотого деления. Даже столы, шкафы, ящики, окна, двери не составляют исключения: в этом легко убедиться, взяв среднее из многих измерений. 6.Закрепление понятия « пропорция» Разминка: У меня в руках 3 прямоугольника. Прямоугольники неравные, но один из них имеет размеры 5х8. На какой из них приятно смотреть?(Ответ: Древние греки считали, что прямоугольники у которых стороны относятся как 5х8 (стороны образуют «золотое сечение») имеют наиболее приятную форму. Снова вспомнить определение пропорции. Творческая работа для учащихся: 1). Составить всем простые пропорции и озвучить по очереди. 2). № 744по учебнику 3). Решение задач: А) Клоун составил следующие пропорции: 1)3 : 6 = 2 : 4 2) 4 : 6 = 2 : 3 Все ли пропорции составлены правильно? Почему? 3) 3 : 6 = 4 : 2 4) 6 : 2 = 4 : 6 5) 6 : 2 = 4 : 6 6) 6 : 4 = 3 : 2 7) 6 : 3 = 4 : 2 8) 8 : 4 = 2 : 3 Б) Почему равенства 1) 1 : 2 = 3 : 6 и 1,2 : 0,3 = 32 : 8 являются пропорциями? 2) 4,2 : 2 = 22 : 10 не является пропорцией? 7. Домашнее задание: №735, 752 выучить определения, придумать примеры предметов, имеющие форму золотого прямоугольника 8. Решение примеров №744,745, 752, 760 9.Творческое задание. Золотое сечение встречается и в растительном мире. На каждом столе лежит рисунок стебля растения. Составьте золотую пропорцию, сделайте необходимые измерения и вычислите коэффициент пропорциональности. 10. Итог урока А). итог по выполненному заданию. Б).ответы на вопросы. 1. Что такое отношение, пропорция? 2. Как называются числа в отношении, пропорции? 3. Что показывает отношение 2-х чисел? В) Составить по изученной теме стихотворение, используя метод развития критического мышления - прием Синквейн – «белый стих, стих не в рифму», все что изучили на уроке представить в 6-7 строках ( 1 строчка- тема, 1 существительное; 2 строчка – определение, 2 прилагательных; 3 строчка – действие, 3 глагола; 4 строчка – ассоциации, 4 существительных; 5 строчка – действие, 3 глагола; 6 строчка – определение, 2 прилагательных; 7 строчка – 1 существительное). У кого что получилось, опрос каждого ученика. Можно предложить такой вариант: отношения равные, однородные делить, преобразовать, сравнить равенство, гармония, соразмерность, соотношение пропорция, члены. Оценка работы каждого учащегося, отметки за урок. Вывод по уроку: Знания, полученные на сегодняшнем уроке, помогут решать все типы задач на проценты с помощью пропорции. Позже с помощью пропорции вы будете решать задачи по химии, физике и геометрии. Литература:
Приложение 1 infourok.ru составление пропорции по условию задачи
Записи с меткой "составление пропорции по условию задачи"Задача 1. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги? Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги: 3,3:300 или х:500. Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений): 3,3:300=х:500. Неизвестный средний член пропорции равен произведению крайних членов пропорции, деленному на известный средний член. (Подробно о пропорции и нахождению ее крайнего, среднего членов читайте в статье: «6.1.1. Пропорция. Основное свойство пропорции.») х=(3,3·500):300; х=5,5. Ответ: пачка 500 листов бумаги имеет толщину 5,5 см. Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде: или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см. Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6 классе. Задача 2. Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды? Решение. Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы. 5:100 или х:98. Получаем пропорцию: 5:100 = х:98. х=(5·98):100; х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды. Задача 3. Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти? Решение. Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти: 16,8:21 или х:35. Получаем пропорцию: 16,8:21=х:35. Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35) и делим на известный средний член (21). Сократим дробь на 7. Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5 (5 и 10) и на 3 (168 и 3). Ответ: 35 литров нефти имеют массу 28 кг. Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля? Решение. Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это: х:100 или 9:18. Составляем пропорцию: х:100 = 9:18. Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9) и делим на известный крайний член (18). Сокращаем дробь. Ответ: площадь всего поля 50 га. www.mathematics-repetition.com 
|
- отношение, а≠0, в≠0,где а и в – члены отношения.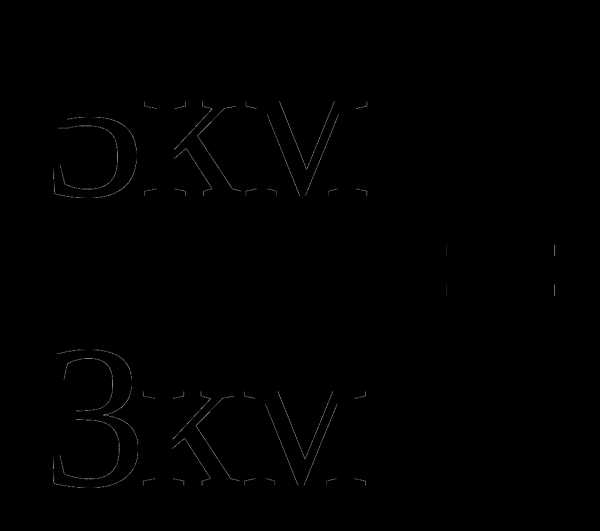
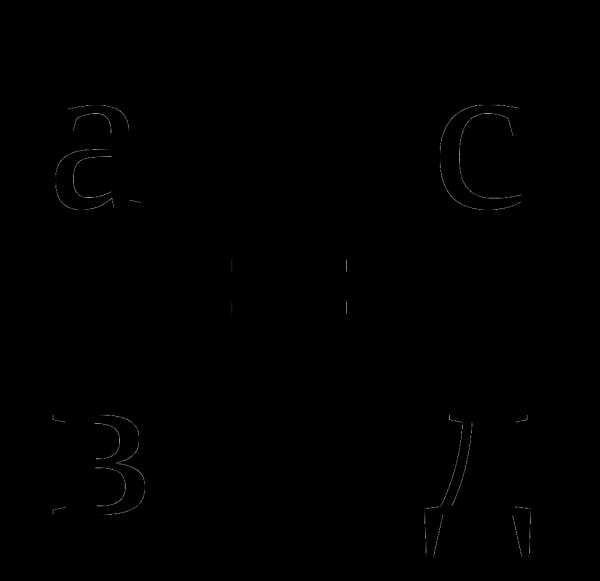где а, в, с, д - члены пропорции, не равные 0.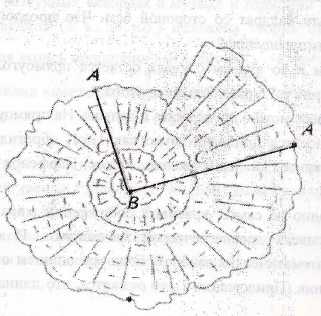
Приложение 2
