Роль моделирования при работе над задачей в 5 классе (стр. 1 из 8). Математические модели 5 класс как объяснить ребенку
Математическое моделирование 5 класс
Дополнения к учебному пособию Математика для 5-го класса под редакцией Л.Б. Шнепермана, в связи с изменениями в программе ● О математическом моделировании для учащихся 5 класса Разные виды математического моделирования самым естественным образом демонстрируются, например, при решении текстовых задач. Так, мы имеем дело с графическими моделями при использовании отрезков для иллюстрирования особенностей условий задач на нахождение двух чисел по их сумме и разности, по их сумме и частному, по их разности и частному (см. соответствующие пункты в учебном пособии). Числовые выражения и выражения с переменными (формулы и уравнения) также могут являться моделями некоторых ситуаций, описанных в задачах. Выражение (числовые или с переменной), составленное по данным задачи, это не что иное, как перевод условия задачи на математический язык – язык цифр, знаков действий и других символов. Полученное в процессе решения задачи равенство двух выражений, т.е. уравнение, – это математическая модель реальной жизненной ситуации, о которой говорится в задаче. Таблицы, схемы, рисунки, чертежи, графики, диаграммы также являются моделями определенных конкретных ситуаций, – учителю следует систематически обращать на это внимание учащихся. ● Множества. Общие элементы и все элементы заданных множеств Несколько объектов, объединенных некоторым признаком, часто называют множеством. Например, можно сказать: множество всех стульев в комнате, множество всех картофелин в данном мешке, множество всех рыб в океане, множество всех букв на этой странице. Объекты, составляющие некоторое множество, называют его элементами. П р и м е р 1. Перечислите элементы множества: а) всех дней недели; б) всех месяцев в году; в) всех арифметических действий. Элемент может принадлежать множеству, и элемент может не принадлежать множеству. Например, апельсин принадлежит множеству фруктов, и апельсин не принадлежит множеству овощей. Множество может не содержать ни одного элемента, – его называют пустое множество. Например, множество учащихся вашего класса, которым больше 17 лет, – пустое. При решении некоторых задач бывает удобно множество изображать графически (использовать графические модели). Для этого можно нарисовать какой-нибудь замкнутый контур, например, овал. Затем отметить внутри этого контура элементы заданного множества, либо, если их слишком много, просто представить, что они находятся там. П р и м е р 2. Заданы: множество букв слова К А Р У С Е Л Ь и множество букв слова К А Р Т О Ф Е Л Ь. Укажите для этих множеств: а) их общие элементы; б) все их элементы. Р е ш е н и е. а) Для множеств букв из слов К А Р У С Е Л Ь и К А Р Т О Ф Е Л Ь общими элементами, т.е. элементами, принадлежащими и первому, и второму множеству, являются буквы:К, А, Р, Е, Л, Ь (их можно было указать и в любом другом порядке).б) Укажем теперь (в любом порядке) все элементы двух этих множеств, т.е. все элементы принадлежащие хотя бы одному из этих множеств: К, А, Р, У, С, Е, Л, Ь, Т, О, Ф.На рисунке 4 в зеленом овале показаны элементы множества букв, из которых состоит слово К А Р У С Е Л Ь, в красном овале – элементы множества букв, из которых состоит слово К А Р Т О Ф Е Л Ь. Общие элементы этих двух множеств, т.е буквы, которые есть в обоих словах, размещены в пересечении внутренних частей этих двух овалов.
У СК А Р Т О ФЕ Л ЬП р и м е р 3. Задано множество двузначных чисел меньших 16 и множество натуральных чисел не меньших 12 и не больших 21. Укажите для этих множеств:а) их общие элементы; б) все их элементы.Р е ш е н и е. а) Общими элементами этих множеств являются числа: 12, 13, 14, 15.б) Все элементы двух этих множеств – числа не меньше 10 и не больше 21, т.е.: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.▲П р и м е р 4. Из 30 детей каждый поёт или танцует. Известно, что петь умеют 17 детей, а танцевать умеют 19 детей. Сколько детей умеют и петь, и танцевать?Р е ш е н и е. Сначала заметим, что из 30 детей не умеют петь 30 – 17, т.е. 13 детей.Все они умеют танцевать, т.к. по условию каждый из детей поёт или танцует. Танцевать умеют всего 19 человек, из них 13 не умеют петь, значит, умеют и танцевать, и петь 19 – 13, т.е. 6 человек. Такой же ответ можно получить иначе:
17 – 11 (от числа детей, умеющих петь, надо вычесть число детей, не умеющих танцевать).Ответ:
6.На рис. 5 зеленым овалом показано множество детей, которые умеют танцевать, а красным овалом – множество детей, которые умеют петь. Пересечением этих овалов изображается множество детей, которые умеют и петь, и танцевать, – их всего 6.▲
Т 30 – 17 = 13 19 – 13 = 6 30 – 19 = 11 П Т и П
▲ П р и м е р 5. В классе 15 учащихся посещают кружок по математике, 12 учащихся – кружок по английскому языку, 5 учащихся – и по математике, и по английскому языку. Сколько учащихся в классе, если каждый из них посещает, либо один кружок, либо два кружка?Р е ш е н и е. Сначала заметим, что из 15 учащихся, которые посещают кружок по математике, 5 учащихся посещают еще кружок по английскому языку, значит 15 – 5, т.е. 10 учащихся посещают только один кружок по математике.Так же можно определить количество учащихся, которые посещают факультатив только по английскому языку:
12 – 5, т.е. 7 учащихся. Число всех учащихся в классе:
10 + 7 + 5, т.е. 22 человека.Ответ:
22.На рис. 6 зеленым овалом показано множество учащихся, которые посещают кружок по математике, а красным овалом – множество учащихся, которые посещают кружок по английскому языку. ▲
М 15 – 5 = 10 5 12 – 5 = 7 А М и АВопросы. 1. Приведите пример множества, состоящего: а) из трех элементов; б) из семи элементов.2. Какое множество называют пустым? Приведите пример пустого множества.3. Приведите пример двух множеств, которые:а) имеют один общий элемент; б) три общих элемента; в) не имеют общих элементов. Перечислите все элементы этих множеств.Упражнения1. Назовите элементы, принадлежащие множеству всех однозначных чисел и элементы, не принадлежащие данному множеству.2. Назовите элементы, принадлежащие множеству съедобных грибов и элементы, не принадлежащие данному множеству.3. Заданы: множество букв слова ГРУША и множество букв слова ШАРИК. Укажите для этих множеств: а) их общие элементы; б) все их элементы.4. Заданы: множество, состоящее из всех однозначных чисел, которые делятся на 2, и множество, состоящее из всех однозначных чисел, которые делятся на 3. Укажите для этих множеств: а) их общие элементы; б) все их элементы.На фирме работают 66 человек. Из них 43 знают французский язык, 35 – немецкий язык. Сколько сотрудников фирмы знают оба языка?Из 40 пятиклассников 32 любят молоко, 21 – лимонад. Сколько пятиклассников любят и молоко, и лимонад?7. В классе 12 учащихся любят читать детективы, 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в классе?8. В классе всего 25 учащихся, каждый из них любит смотреть или комедии, или мультфильмы, или и то и другое. Из тех 18 учащихся, которые любят смотреть комедии, только 12 не прочь посмотреть и мультфильмы. Сколько человек в классе любят смотреть только мультики?9. Из 29 мальчишек, живущих в одном доме, только двое не занимаются спортом, а остальные посещают или футбольную, или теннисную секции, или обе. Футболом занимается 17 мальчишек, а теннисом – 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?10. В классе всего 25 учащихся. Из них 7 любят груши, 11 – апельсины. Двое любят груши и апельсины;
6 – груши и яблоки;
5 – яблоки и апельсины. Но есть в классе два ученика, которые любят и груши, и яблоки, и апельсины и четверо таких, что не любят никакие из этих фруктов. Сколько учащихся этого класса любят яблоки?После изучения материала главы 4 Делимость натуральных чисел по теме Множества. Общие элементы и все элементы заданных множеств можно решать следующие упражнения.П р и м е р 1. Задано множество всех делителей числа 16 и множество всех делителей числа 30. Укажите для этих множеств:а) их общие элементы; б) все их элементы.Р е ш е н и е. Множество всех делителей числа 16:
1, 2, 4, 8, 16.Множество всех делителей числа 30:
1, 2, 3, 5, 6, 10, 15, 30.а) Общими элементами этих множеств являются числа:
1, 2.б) Все элементы двух этих множеств – числа 1, 2, 3, 4, 5, 6, 8, 10, 15, 16, 30.П р и м е р 2. Задано множество двузначных кратных числа 18 и множество двузначных кратных числа 24. Укажите для этих множеств:а) их общие элементы; б) все их элементы.Р е ш е н и е. Множество двузначных кратных числа 18:
18, 36, 54, 72, 90.Множество двузначных кратных числа 24:
24, 48, 72, 96.а) Общим элементом этих множеств является число:
72.б) Все элементы двух этих множеств – числа 18, 24, 36, 48, 54, 72, 90, 96.Упражнения.1.Найдите множества всех делителей чисел 40, 60. Укажите для этих множеств:а) их общие элементы; б) все их элементы.2. Найдите множества всех делителей чисел:1) 20 и 30;
2) 50 и 125;
3) 60 и 90;
4) 18 и 45.Укажите для этих множеств: а) их общие элементы; б) все их элементы.3. Найдите множества всех делителей чисел 24, 30, 45. Укажите для этих множеств: а) их общие элементы; б) все их элементы.4. Найдите множество всех двузначных кратных числу 15 и множество всех двузначных кратных числу 12. Укажите для этих множеств: а) их общие элементы; б) все их элементы.5. Найдите множество всех двузначных кратных числу 20 и множество всех двузначных кратных числу 40. Укажите для этих множеств: а) их общие элементы; б) все их элементы.После изучения материала главы 5 Простые числа по теме Множества. Общие элементы и все элементы заданных множеств можно решать следующие упражнения.П р и м е р 1. Задано множество простых чисел не меньше 19 и не больше 43 и множество простых чисел не меньше 31 и не больше 59. Укажите для этих множеств:а) их общие элементы; б) все их элементы.Р е ш е н и е. Множество простых чисел не меньше 19 и не больше 43:
19, 23, 29, 31, 37, 41, 43.Множество простых чисел не меньше 31 и не больше 59:
31, 37, 41, 43, 47, 53, 59.а) Общими элементами этих множеств являются числа:
31, 37, 41, 43.б) Все элементы двух этих множеств – числа:
19, 23, 29, 31, 37, 41, 43, 47, 53, 59.Упражнения Найдите множество простых чисел не меньше 101 и не больше 109 и множество простых чисел не меньше 83 и не больше 113. Укажите для этих множеств: а) их общие элементы; б) все их элементы.Найдите множество составных чисел не меньше 3 и не больше 11 и множество составных чисел не меньше 7 и не больше 13. Укажите для этих множеств: а) их общие элементы; б) все их элементы.Найдите множество всех делителей числа 308 и множество всех делителей числа 385. Укажите для этих множеств: а) их общие элементы; б) все их элементы. Найдите НОД (308, 385).Числа 70, 30 и 110 разложили на простые множители и выписали для каждого из этих чисел множество полученных простых множителей. Укажите для этих трех множеств: а) их общие элементы; б) все их элементы. Найдите множество всех двузначных чисел, кратных числу 15 и множество всех двузначных чисел, кратных числу 30. Укажите для этих множеств: а) их общие элементы; б) все их элементы. Материалы для организации самостоятельной работы учащихся по теме Множества. Общие элементы и все элементы заданных множествПосле изучения материала главы 2 Сложение и вычитание натуральных чисел можно провести СР 1.СР 1. Вариант 1.Укажите верное утверждение:а) число 10 принадлежит множеству всех однозначных чисел;б) число 10 не принадлежит множеству всех однозначных чисел.2. Заданы: множество букв слова КОТИК и множество букв слова КОФТА. Укажите для этих множеств: а) их общие элементы; б) все их элементы.3. Заданы: множество, состоящее из всех двузначных чисел, которые делятся на 20, и множество, состоящее из всех двузначных чисел, которые делятся на 30. Укажите для этих множеств: а) их общие элементы; б) все их элементы.4. В лыжных соревнованиях в забегах на 1 км и 3 км участвовали 35 спортсменов. Из них 21 спортсмен бежали дистанцию 1 км, 23 – дистанцию 3 км. Сколько спортсменов бежали обе дистанции?5. В классе 15 учащихся посещают факультатив по математике, 17 – факультатив по английскому языку, 4 – посещают оба эти факультатива. Сколько учеников в классе?СР 1. Вариант 2.Укажите верное утверждение:а) число 10 принадлежит множеству всех двузначных чисел;б) число 10 не принадлежит множеству всех двузначных чисел.2. Заданы: множество букв слова ЗАБОР и множество букв слова ЗАМОК. Укажите для этих множеств: а) их общие элементы; б) все их элементы.3. Заданы: множество, состоящее из всех двузначных чисел, которые делятся на 10, и множество, состоящее из всех двузначных чисел, которые делятся на 15. Укажите для этих множеств: а) их общие элементы; б) все их элементы.4. На велогонках в заездах приняли участие 42 спортсмена. Из них 29 спортсменов проехали дистанцию в 3 км, 26 – дистанцию в 5 км. Сколько спортсменов проехали обе дистанции?5. В классе 18 учащихся посещают факультатив по французскому языку, 15 – факультатив по немецкому языку, 6 – посещают оба эти факультатива. Сколько учеников в классе?После изучения материала главы 4 Делимость натуральных чисел можно провести СР 2.СР 2. Вариант 1.1. Укажите множество всех делителей числа 18.а) 1, 2, 3, 9, 18;б) 2, 3, 6, 9, 18;в) 1, 2, 3, 6, 9;г) 1, 2, 3, 6, 9, 18.2. Найдите множество всех делителей чисел 20 и множество всех делителей чисел 24. Укажите для этих множеств:а) их общие элементы; б) все их элементы.3. Найдите множество всех двузначных чисел, кратных числу 16, и множество всех двузначных чисел, кратных числу 24. Укажите для этих множеств: а) их общие элементы; б) все их элементы.4. Найдите множества всех делителей чисел 28, 56, 98. Укажите для этих множеств: а) их общие элементы; б) все их элементы.5. Числа 4373 и 826 разделили на одно и то же натуральное число и получили в остатках 8 и 7 соответственно. На какое число делили?СР 2. Вариант 2.1. Укажите множество всех делителей числа 24.а) 2, 4, 6, 12, 24;б) 1, 2, 4, 6, 12;в) 1, 2, 4, 6, 24;г) 1, 2, 4, 6, 12, 24.2. Найдите множество всех делителей чисел 36 и множество всех делителей чисел 42. Укажите для этих множеств:а) их общие элементы; б) все их элементы.3. Найдите множество всех двузначных чисел, кратных числу 18, и множество всех двузначных чисел, кратных числу 36. Укажите для этих множеств: а) их общие элементы; б) все их элементы.4. Найдите множества всех делителей чисел 24, 36, 28. Укажите для этих множеств: а) их общие элементы; б) все их элементы.5. Числа 1049 и 1865 разделили на одно и то же натуральное число и получили в остатках 5 и 9 соответственно. На какое число делили?
После изучения материала главы 5 Простые числа можно провести СР 3.СР 3. Вариант 1.1. Укажите множество простых чисел от 3 до 17.а) 3, 5, 11, 13, 17;б) 3, 5, 7, 11, 13;в) 3, 5, 7, 11, 13, 17;г) 3, 5, 7, 11, 17.2. Найдите множество простых чисел не меньше 83 и не больше 101 и множество простых чисел не меньше 89 и не больше 107. Укажите для этих множеств: а) их общие элементы; б) все их элементы.3. Среди всех делителей для каждого из чисел 30 и 105 найдите те, которые являются простыми числами. Укажите для этих двух множеств: а) их общие элементы; б) все их элементы. 4. Числа 66 и 165 разложите на простые множители. Укажите для двух множеств, состоящих из всех делителей этих чисел: а) их общие элементы; б) все их элементы. Найдите НОД (66, 165).5. Произведение четырех последовательных чисел равно 5040. Найдите эти числа.СР 3. Вариант 2.1. Укажите множество простых чисел от 37 до 47.а) 31, 41, 43, 47;б) 37, 41, 43, 47;в) 31, 37, 41, 43;г) 31, 37, 41, 43, 47.2. Найдите множество простых чисел не меньше 131 и не больше 149 и множество простых чисел не меньше 109 и не больше 137. Укажите для этих множеств: а) их общие элементы; б) все их элементы.3. Среди всех делителей для каждого из чисел 50 и 165 найдите те, которые являются простыми числами. Укажите для этих двух множеств: а) их общие элементы; б) все их элементы.4. Числа 78 и 273 разложите на простые множители. Укажите для двух множеств, состоящих из всех делителей этих чисел: а) их общие элементы; б) все их элементы. Найдите НОД (78, 273).5. Произведение четырех последовательных чисел равно 1680. Найдите эти числа.● При изучении материала пункта 3.12 Числовые выражения уместно добавить материал о прикидке результата вычислений.При нахождении значения числового выражения для самопроверки бывает полезно сначала округлить данные числа и найти его значение приближенно. Такую операцию называют прикидкой результата действия. Прикидку выполняют и тогда, когда вызывает сомнение результат уже выполненных вычислений.Соответственно, можно предложить решать такого типа упражнения:Верно ли найдено значение числового выражения:40 ∙25318 + 30 ∙ 15360 + 20 ∙ 2740 = 5659000?Р е ш е н и е. Сделаем прикидку результата, для чего все вторые множители в указанном выражении округлим до разряда тысяч. Получим:40 ∙25318 + 30 ∙ 15360 + 20 ∙ 2740 ≈ 40 ∙ 25000 + 30 ∙ 15000 + 20 ∙ 3 000 == 1 000000 + 450 000 + 60 000 = 1510000.Очевидно, что значение числового выражения, указанное в условии, – ошибочное. Ответ. Неверно.Упражнения1. Верно ли (ответ объясните), что:1) 80 ∙41 300 + 20 ∙ 64 980 + 60 ∙ 81 020 > 8365000;2) 200 ∙710 300 + 300 ∙ 146 150 + 400 ∙ 227 500 2. Пользуясь прикидкой результата действия, сравните:1) 368 + 482 и 1000;
2) 259 + 415 и 600;3) 1463 + 3841 и 6000;
4) 3216 + 5764 и 8000;5) 32 46 и 1400;
6) 74 26 и 2000;7) 154 391 и 80000;
8) 367 653 и 200000.3. 1) Расстояние между городами 450 км. Сможет ли автомобиль, движущийся со скоростью 78 км/ч, проехать за:а) 5 ч;б) 6 ч?2) В книге 365 страниц. Ваня читает ежедневно по 18 страниц. Сможет ли Ваня прочитать эту книгу за:а) 19 дней; б) 21 день?● О признаке делимости на 4Очевидно, что если натуральное число делится на 100, то оно делится и на 4. Число, которое не оканчивается двумя нулями, например, 31872, представим как сумму двух слагаемых:31872 = 31 800 + 72.Оба слагаемых делятся на 4. Следовательно, и сумма делится на 4.Возьмем еще одно число, которое не оканчивается двумя нулями, и представим его как сумму двух чисел:
31813 = 31 800 + 13.Поскольку второе слагаемое 13 не делится на 4, то и сумма не делится на 4. Таким образом, на 4 делятся числа, которые оканчиваются двумя нулями или у которых две последние цифры выражают число, делящееся на 4. Это и есть признак делимости на 4. Заметим, что никакие другие числа на 4 не делятся.Упражнения1. Какие из чисел 108, 226, 3214, 4156, 394516, 72361196 делятся на 4?2. Выпишите подряд, начиная с числа 512, пять натуральных чисел, делящихся на число 4.3. Используя цифры 0, 2, 4, 8 не более одного раза каждую, составьте все возможные трехзначные числа, которые кратны 4.4. Из чисел 636, 840, 98, 62, 7, 4, 2720, 64 830, 130 026, 130 264, 52 136, 67 456 выпишите:в порядке возрастания числа, делящиеся на 4;в порядке убывания числа, не делящиеся на 4.Запишите все однозначные числа, кратные числу 4.Запишите все двузначные числа от 57 до 68 не кратные 4.Вместо символа ☺ в числах26☺, 3☺0, 61☺, 37☺4, 2☺92, 49☺, 2☺32, 371☺поставьте цифру (если возможно—несколькими способами) так, чтобы полученное число делилось на 4.Используя цифры 0, 4 и 6 составьте все возможные трехзначные числа кратные 4.Используя по одному разу каждую из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 составьте наибольшее десятизначное число, кратное 4.11. Найдите сумму всех чисел, которые делятся на 4 и расположены в натуральном ряду между числами (т.е. таких чисел, которые больше первого и меньше второго из указанных чисел):1) 4 и 18; 2) 19 и 30;
3) 124 и 133; 4) 4799 и 4816.Материалы для организации самостоятельной работы учащихся по теме Признак делимости на 4После изучения признака делимости на 4 можно провести СР 4СР 4. Вариант 1.Укажите число, которое не делится на 4.а) 32232232;б) 265816;в) 1632028;в) 764562.Найдите сумму всех натуральных чисел, которые расположены в натуральном ряду между числами 34 и 50 (т.е. чисел больших 34 и меньших 50) и делятся на 4.Для числа 89319 найдите ближайшее к нему в натуральном ряду число, которое кратно 4.Найдите наименьшее трехзначное число такое, сумма этого числа и числа 39 делилась бы на 4.Запишите наибольшее семизначное число, которое состоит из четных цифр и делится на 4.СР 4. Вариант 2.Укажите число, которое делится на 4.а) 56454202;б) 391 538;в) 39818 910;в) 986 364.Найдите сумму всех натуральных чисел, которые расположены в натуральном ряду между числами 43 и 60 (т.е. чисел больших 43 и меньших 60) и делятся на 4.Для числа 57 307 найдите ближайшее к нему в натуральном ряду число, которое кратно 4.Найдите наименьшее трехзначное число такое, сумма этого числа и числа 25 делилась бы на 4.Запишите наибольшее восьмизначное число, которое состоит из четных цифр и делится на 4.
www.freedocs.xyz
Как объяснить математические модели в школе?
Л. Д. Кудрявцев обоснованно считает, что «в курсе математики изучаются математические модели».
И действительно, любое понятие школьного курса математики представляет собой математическую модель. Идея моделирования, идея математической модели является одной из основных идей математики. А известна ли она ученикам? Знают ли ученики, что они изучают и оперируют с мат. моделями?
 Многочисленные опросы учащихся, проведенные нами и другими исследователями, показали, что учащиеся этого не знают. На вопрос: «Что такое модель?» — они дают самые невразумительные ответы или вообще ничего сказать не могут, а в качестве примеров моделей указывают лишь на модели геометрических тел, стоящие в шкафах математического кабинета. На вопрос: «Приведите примеры математических моделей» — учащиеся опять-таки ссылаются на указанные модели геометрических тел, хотя в самом деле они ими не являются.
Многочисленные опросы учащихся, проведенные нами и другими исследователями, показали, что учащиеся этого не знают. На вопрос: «Что такое модель?» — они дают самые невразумительные ответы или вообще ничего сказать не могут, а в качестве примеров моделей указывают лишь на модели геометрических тел, стоящие в шкафах математического кабинета. На вопрос: «Приведите примеры математических моделей» — учащиеся опять-таки ссылаются на указанные модели геометрических тел, хотя в самом деле они ими не являются.
Другим примером, демонстрирующим указанное заблуждение, является утверждение, что продуманная система арифметических задач и упражнений позволит ввести уже в младших классах функции и уравнения, комбинаторику и алгоритмы». Так, утверждается, что если учащиеся составят таблицу, впервой строке, которой будут выписаны подряд первые натуральные числа, а во второй строке — их суммы с числом 3, то «такая таблица заключает в себе идею функциональной зависимости — она является таблицей значений функций у=3+х».
Если же учащиеся будут производить сложение или вычитание чисел, заданных в таблице, то они якобы будут знакомиться с действиями над векторами, и тем самым, решая подобные арифметические примеры, «учащиеся будут овладевать идеями современной математики».
Заблуждение состоит в том, что ученики об этих идеях, которые действительно имеются в этих примерах, но имеются для них неявно, не догадываются и не могут догадываться. Поэтому они этими идеями, конечно, не овладевают. То, что сложение чисел по столбцам представляет собой сложение векторов, заданных своими координатами, знает учитель, но для учеников это действие есть обычное сложение чисел и не более. В психологии давно доказано следующее фундаментальное положение:
Это положение следует понимать так. Для этого еще необходимо, чтобы это содержание стало целью действий субъекта.
Когда ученик складывает числа, пусть по столбцам или иначе, то целью его действия является нахождение сумм, и, хотя в поле его восприятия находилось и сложение координат векторов, он это не осознает и, следовательно, не усваивает. Вот если бы учитель специально обратил его внимание именно на эту сторону данного примера и сделал бы целью его действий нахождение суммы координат векторов, то тогда бы ученик осознал — это действие как сложение векторов. Но для этого, очевидно, ученика следует предварительно познакомить с понятием вектора, координат вектора и т. д., что вряд ли является целесообразным в условиях начальных классов.Отсюда следует, что для того, чтобы учащиеся усвоили и овладели основными идеями и методами современной математики, лежащими в основе школьного курса, необходимо ввести эти идеи и методы в содержание обучения в явном виде и сделать их усвоение целью действий учащихся.
Проблема конструирования содержания обучения математике является комплексной и может быть правильно разрешена лишь при учете как психолого-педагогических, так и методико-математических результатов ее анализа.
При конструировании содержания обучения и при его осуществлении в практике обучения следует исходить из непосредственной цели обучения математике и тех условий, при которых это обучение может сыграть свою значительную роль в решении задач общего образования.
Ко всем этим положениям мы еще неоднократно будем в следующих постах возвращаться и при этом постараемся их конкретизировать. А с современными технологиями все это можно реализовать еще быстрее и качественнее, вот, например, электронный дневник, который облегчает работу учителя и помогает следить за оценками ребенка родителям.
Материалы по теме:
Поделиться с друзьями:
Загрузка... matemonline.com
Урок в 5 классе по теме: "Математическая модель" (ФГОС).
Вы талантливые, дети! Когда–нибудь вы сами приятно поразитесь, какие вы умные, как много вы умеете, если будите постоянно работать над собой, ставить новые цели и стремиться к их достижению. Девочки и мальчики садитесь, пожалуйста.
Меня зовут Светлана Николаевна.
Я проведу урок математики.
Проверим готовность.
Демонстрирует презентацию.
Слайд 1.
Запишем дату и классная работа. Подготовим тетради для работы.
Какое нужно настроение, чтобы наш урок получился удачным?
Я желаю вам сохранить хорошее настроение на весь урок.
Слайд 2.
Предлагает решить ребус.
Слайд 3.
Задает вопросы:
Где в реальной жизни вы встречались с моделями?
Ребята, а вы знаете, что такое модель?
Записывает варианты на доске.
Слайд 4.
Представьте ситуацию, что вам надо создать модель самолета. Какие действия вы будете совершать?
Подводит итог: Деятельность человека по созданию модели называется моделированием.
Слайд 5.
Организует беседу.
Вопросы:
Что такое текстовая задача?
Какие действия вы будете совершать, если я предложу вам решить эту задачу?
Что вы будете использовать? Каким языком пользоваться?
Из чего состоит математический язык (что он содержит)?
Направляет учеников на формулировку нового понятия «математическая модель», на формулировку темы урока.
Вопросы:
Итак, в процессе решения задачи от реальной ситуации мы переходим с вами к составлению чего? (проведите аналогию с самолетом).
На уроке математике, как вы думаете, о каких моделях пойдет речь?
Что же такое математическая модель?
Выслушивает варианты учеников.
Записывает варианты на доске.
Направляет к правильной формулировке.
Скажите, одну и ту же задачу вы все будете решать одинаково?
А какие существуют способы?
Слайд 6.
Математическая модель – это способ описания реальной жизненной ситуации с помощью математического языка.
Вопрос:
Кто может назвать тему сегодняшнего урока?
Слайд 7.
Рассказывает о листе обратной связи, напоминает, как с ним работать.
Задает вопросы и записывает ответы учеников на доске:
Что нужно узнать по теме урока? Какие умения будем у себя формировать?
Записывают дату. Слушают.
Решают ребус.
Отвечают на вопросы.
(Да, модели машинок, самолетов, игрушки и т.д.)
Аналог реального объекта)
Отвечают на вопросы, участвуют в дискуссии, слушают.
(Строим, находим чертеж, выбираем материал, собираем, склеиваем и т.д.)
Отвечают на вопросы, участвуют в дискуссии, слушают.
(описание реальной ситуации из жизни)
(Читаю условие, составляю краткую запись в виде таблицы, схемы, чертежа и т.д., записываю решение в виде числового выражения, буквенного выражения, уравнения).
(Математический язык)
(цифры, латинские буквы, знаки действий, скобки, запятые, специальные символы)
(математической модели)
Формулирует, что такое математическая модель (варианты учащихся).
Читают, воспринимают, запоминают, записывают.
Называют тему.
Подписывают лист обратной связи, записывают тему урока.
Отвечают на вопросы и записывают умения в листе обратной связи.
(узнавать математические модели; составлять по словесному описанию математическую модель; описывать математическую модель).
Позитивный настрой на учебную деятельность.
Актуализация знаний (понятий: текстовая задача, математический язык).
Формулировка нового понятия (математическая модель).
Формулировка темы урока.
Названы и записаны умения, которые будут формироваться на уроке.
2.Планирование и организация деятельности (25 мин).
Демонстрирует презентацию и дает задания ученикам.
Слайд 8
Задание №1.
Найдите среди предложенных моделей математические модели?
На формирование какого умения направлено это задание?
Напоминает о фиксации в листе обратной связи.
Организует фронтальную работу со всем классом.
Задает вопросы:
Какие выражения называются буквенными?
Что такое формула?
Слайды 9 -10.
Объясняет правила работы в паре. Дает инструкцию.
Вызывает учеников к доске.
Задания № 2 и 3.
Организует проверку.
Вы согласны с решением на доске?
В чем ошибка? Почему?
На формирование какого умения направлено это задание?
Напоминает о фиксации в листе обратной связи.
Слайд 11.
Физкультминутка.
Называет различные модели (математические и не математические).
Дает инструкцию.
Ребята, все готовы писать самостоятельную работу? У всех напротив умений стоят плюсы?
Слайд 12.
Задание № 4.
Организует индивидуальную работу (дифференцированные задания).
Раздает карточки успешным ученикам.
Организует проверку по образцу.
Проверяет задания на карточках.
Слайд 13.
Организует самостоятельную работу (первичный контроль).
Раздает карточки. Время 3 мин.
Отвечают на вопросы.
Оценивают свои достижения.
Читают задание.
Выполняют задания.
Обсуждают решение в паре.
Работают у доски.
Оценивают свои достижения.
Узнают математические модели.
Выполняют упражнения.
Читают задание.
Выполняют индивидуальные задания.
Проверяют свою работу.
Оценивают свои достижения.
Выполняют предложенные задания самостоятельно.
Формирование умений: узнавать математические модели; составлять по словесному описанию математическую модель; описывать математическую модель.
Рефлексия (5 мин).
Организует самопроверку по образцу.
Слайды 14 – 15.
Напоминает о фиксации в листе обратной связи.
Поднимите руки, кто все задания выполнил правильно?
Поставьте себе «5».
Поднимите руки, кто выполнил правильно одно задание из двух?
Поставьте себе «4».
Подведем итог урока.
Какова была тема урока?
Что нового узнали на уроке?
Чему научились на уроке?
С какими трудностями столкнулись?
А что делать тем, у кого не все пока получилось?
Дома: Слайд 16.
Для тех, кто пока не поставил себе оценку за урок: № 275, № 276 (а – 1 выражение)
Для тех, кто поставил себе за урок «4»: или № 275 или № 276 (б).
Для тех, кто поставил себе «5»: составить карточку с заданиями для проверки отрабатываемых на уроке умений. Решение записать в тетрадь.
Спасибо вам за урок!
Сличают свои решения с образцом.
Отвечают на вопросы.
Оценивают свою деятельность.
Выбирают задание для домашней работы.
Записывают домашнее задание.
Осознание обучающимися своей учебной деятельности;
самооценка результатов своей деятельности.
infourok.ru
презентация урока математики в 5 классе по теме "Математические модели"
Инфоурок › Математика › Презентации › Презентация урока математики в 5 классе по теме "Математические модели" Описание презентации по отдельным слайдам:
1 слайд 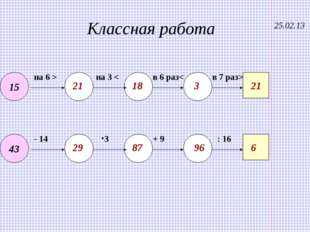 Описание слайда:
Описание слайда: Классная работа 25.02.13 21 18 3 21 29 87 96 6
2 слайд  Описание слайда:
Описание слайда: S = 120 км t = 4 ч v = ? (км/ч) v= s:t v=120:4=30(км/ч) S = 45 км v1 = 3(км/ч) v2 = 6 (км/ч) t = ? ч vсб=v1+v2 t=s:(v1+v2) t=45:(3+6)=5 (ч)
3 слайд 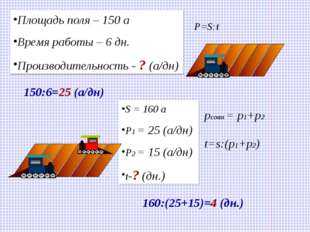 Описание слайда:
Описание слайда: Площадь поля – 150 а Время работы – 6 дн. Производительность - ? (а/дн) 150:6=25 (а/дн) S = 160 а P1 = 25 (а/дн) P2 = 15 (а/дн) t-? (дн.) P=S:t t=s:(p1+p2) pсовм = p1+p2 160:(25+15)=4 (дн.)
4 слайд  Описание слайда:
Описание слайда: Математические модели. Модель – аналог, «заменитель» реального объекта. Математика – наука, которая описывает закономерные связи количественные отношения объектов реального мира. Математика разговаривает на «математическом» языке Математический язык содержит: цифры, латинские и греческие буквы, знаки действий и отношений, скобки, запятые, специальные символы…
5 слайд  Описание слайда:
Описание слайда: Математическая модель – это «заменитель», записанный на языке математике. Числовые и буквенные математические выражения – это ММ Где мы встречались с ММ ? 160:(25+15) t=s:(v1+v2) 45:(3+6) Что будем изучать на уроке? Чему сегодня будем учиться?
6 слайд  Описание слайда:
Описание слайда: задача Расстояние 180 км легковой автомобиль может преодолеть за 2 ч, а грузовому автомобилю на то же расстояние требуется 3 ч. Через какое время они смогут встретиться, если выедут навстречу друг другу из пунктов расстояние между которыми 300 км ? S = 180 км t= ? ч t2 = 3 ч Sн = 300 км v1= s:t1; v2= s:t2; t=sн:vсб; t1 = 2 ч vсб=v1+v2; ? Решение 1). 180:2=90(км/ч) - v1 2). 180:3=60(км/ч) – v2 3). 90+60=150 (км/ч) - vсб 4). 300: 150=2(ч) - t 300:(180:2+180:3)=2(ч) – время, через которое встретятся. Ответ: через 2 ч.
7 слайд  Описание слайда:
Описание слайда: задача Одной бригаде трактористов, чтобы вспахать 180 а, требуется 2 дня, а другой - 3 дня. За какое время эти бригады смогут вспахать 300 а, работая одновременно? S = 180 а tс= ? дн t2 = 3 дн Sн = 300 а p1= s:t1; p2= s:t2; t=sн:pс; t1 = 2 дн pс=p1+p2; ? Решение 1) . 180:2=90(а/дн) - p1 2). 180:3=60(а/дн) – p2 3). 90+60=150 (а/дн) - pс 4). 300: 150=2(дн) - t 300:(180:2+180:3)=2(дн) – время совместной работы. Ответ: через 2 дн.
8 слайд  Описание слайда:
Описание слайда: 300:(180:2+180:3)=2 Это математическая модель реальной жизненной ситуации, которая рассматривалась в задачах Всего в вазе 30 штук фруктов. Апельсинов 2 раза больше, чем бананов. Апельсинов на 10 больше чем бананов Расшифруйте математические модели
9 слайд  Описание слайда:
Описание слайда: а+в=35 а=3в в=а:2 Составьте математические модели в соответствии с каждой ситуацией
10 слайд  Описание слайда:
Описание слайда: Самостоятельная работа 1) Ов.- а ж. К. – в ж. Всего 30 ж. а + в = 30 3 2) П.- а км. В.- в км, в 3 раза > в = 3а 2
11 слайд  Описание слайда:
Описание слайда: Проверка самостоятельной работы
Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Краткое описание документа:
Урок проведен в рамках заседания методического объединения учителей Центрального района города Барнаула. Тема: "Актуальные вопросы применения учителями математикиновых информационных технологий на уроках и во внеурочной работе"
Цель данного урока:
- формировать умение переводить словестные предложения в буквенные выражения и объяснять значения буквенных выражений;
- развивать умение правильно читать выражения, составлять по заданному условию числовые или буквенные выражения, описывать выражения на математическом языке.
-благодаря компьютеру реализовать принципы наглядности, научности и доступности.
Общая информация
Номер материала: 107749
Похожие материалы
Оставьте свой комментарий infourok.ru
Математический язык и математическая модель. Математика, 5 класс: уроки, тесты, задания.
|
1.
|
Запиши на математическом языке
Сложность:
лёгкое
|
1
|
|
2.
|
Переход от обычной речи к математической
Сложность:
лёгкое
|
1
|
|
3.
|
Запиши на обычном языке
Сложность:
лёгкое
|
1
|
|
4.
|
Составление математической модели
Сложность:
лёгкое
|
1
|
|
5.
|
Запиши формулу вычисления заданной величины
Сложность:
среднее
|
2
|
|
6.
|
Выбери соответствующее выражение
Сложность:
среднее
|
2
|
|
7.
|
Утверждение на математическом языке
Сложность:
среднее
|
2
|
|
8.
|
Текстовая задача (каменщик и ученик)
Сложность:
среднее
|
2
|
|
9.
|
Математическая модель движения по течению реки
Сложность:
сложное
|
3
|
|
10.
|
Расстояние между городами
Сложность:
сложное
|
4
|
|
11.
|
Расшифруй математическую модель
Сложность:
сложное
|
3
|
|
12.
|
Составь математическую модель числа как сумму разрядных слагаемых
Сложность:
сложное
|
3
|
www.yaklass.ru
Зачем нужна математика? Для чего изучать, польза от занятий математикой
Сможете ли вы доступно объяснить ребёнку, для чего ему нужно заниматься математикой? Ведь изучение понятий, законов математики и логики, решение математических и логических задач требует умственных усилий. А зачем вообще это нужно?
Мы изучили ряд научных исследований, и выделили реальные доказательства пользы от занятий математикой.
Даже если вы убеждены, что жизнь вашего ребенка не будет связана с математикой, рекомендуем все равно прочитать нашу статью, чтобы как минимум с легкостью ответить на вопросы маленького «почемучки».
1. Математика развивает мышление
Изучая математику и решая задачи, ребёнок учится:
- обобщать и выделять важное;
- анализировать и систематизировать;
- находить закономерности и устанавливать причинно-следственные связи;
- рассуждать и делать выводы;
- мыслить логически, стратегически и абстрактно.
Как регулярные спортивные тренировки «прокачивают» тело, делают его здоровым, сильным и выносливым, так регулярные занятия математикой «прокачивают» мозг – развивают интеллект и познавательные способности, расширяют кругозор.
Математика закладывает навыки эффективного и быстрого обучения чему угодно. Все это происходит благодаря «превращению в человека мыслящего».
Читайте также: В статье «5 причин научиться думать как математик» мы подробно разобрали в чем заключается сила математического мышления и зачем его развивать. 2. Занятия математикой тренируют память
Ученые из Стэнфордского университета в США изучили процесс решения человеком математических задач и выяснили, что взрослые люди используют для этих целей мышление и доведенный до автоматизма навык «доставать» из памяти уже имеющиеся там ответы.
Дети до 7 лет часто прибегают к помощи пальцев рук и ног, а также различных заменителей (реальных предметов, счетных палочек). В «переходный период», в возрасте от 7 до 9 лет, у школьников формируется «взрослый» навык «думания», осмысления и запоминания информации.
Интересное исследование было опубликованно в журнале «Nature Neuroscience» в 2014 году. В первую очередь, оно было посвящено изучению роли гиппокампа (области в головном мозге) в развитии познавательной активности детей. Но его косвенные выводы таковы:
- если хотите, чтобы у ребенка в школе не было проблем с математикой – тренируйте память в раннем возрасте;
- решение математических задач развивает память.
3. Математика закаляет характер
Для правильного решения математических и логических задач нужны внимательность, настойчивость, ответственность, точность и аккуратность.
Чем регулярнее ребенок тренирует эти «мышцы характера», тем сильнее они становятся, тем чаще помогают ребенку в решении не только учебных задач, но и жизненных проблем.
4. Музыка для математики, математика – для музыки
Комплексное исследование, проведенное Барбарой Хелмрич (Barbara H. Helmrich) из Колледжа Нотр-Дам в Балтиморе, выявило, что дети, которые играли на музыкальных инструментах в средней школе, ощутимо лучше успевают по математике в старших классах. Ученые обнаружили, что за решение алгебраических задач и обработку музыкальной информации отвечает один и тот же участок головного мозга.
«Наибольшая средняя разница в результатах по алгебре между любыми двумя группами испытуемых была обнаружена между афроамериканскими «инструментальными» группами и группами «немузыкальных» школьников».
Парадоксально, но ученые как будто не интересовались обратной связью.
Ведь если за развитие математических и музыкальных способностей отвечает один и тот же участок головного мозга, не исключено, что занятия математикой улучшают музыкальные способности.
Вспоминается Шерлок Холмс, который был одновременно превосходным сыщиком и талантливым скрипачом. Многие скажут, что знаменитый английский сыщик – просто выдумка, но у него был свой реальный прототип, наставник и друг Артура Конана Дойла. Страстным скрипачом был и величайший физик Альберт Эйнштейн.
5. Математика помогает преуспевать в гуманитарных науках
Именно ранние математические способности – верная предпосылка к тому, что в дальнейшем ребенок будет не только хорошо понимать математику, но и преуспевать в других школьных дисциплинах. Далее по значимости вклада в учебные успехи идут навыки чтения и способности управлять своим вниманием.
К таким выводам пришли ученые в области образования и социальной политики Северо-Западного университета в Эванстоне. В ходе исследования они оценивали связь ключевых элементов готовности к школе (базовые навыки для приема в школу - «академическая» готовность, внимание, социально-эмоциональные навыки) с дальнейшими успехами в учебе.
Математика – наука междисциплинарная, она тесно связана с физикой, географией, геологией, химией. Социология и экономика неотделимы от математики, и многие выводы даже привычно гуманитарных наук, таких как лингвистика, журналистика, опираются на математические модели и понятия, математические и логические законы.
6. Развивает навыки решения бытовых задач
Барбара Оакли, доктор технических наук, исследователь стволовых клеток мозга и автор книги «Думай как математик» подчеркивает:
«Математика избавляет нас от «магического мышления» – мы стремимся вникнуть в суть вещей и не полагаемся на авось и высшие силы».
Чем сложнее становятся математические задачи, тем больше навыков требуется для их решения. Ребенок учится рассуждать, выстраивать последовательности, продумывать алгоритмы, жонглировать сразу несколькими понятиями, и эти навыки входят в привычку.
Благодаря математике мы избавляемся от вредных привычек:
- не домысливаем, а оперируем только точными терминами;
- не просто механически запоминаем информацию и правила, а оцениваем ее, анализируем, размышляем, чтобы понять и усвоить новый материал, новый жизненный урок.
7. Математика – основа успешной карьеры
Если 10-15 лет назад перспективным считалось изучение иностранных языков, то сейчас свободным владением несколькими языками никого не удивишь. Теперь профессиональная востребованность во многом зависит от понимания технологий, умения мыслить, абстрагироваться и способностей к решению нестандартных задач. Крайне сложно обойтись без знания математики тем, кто хочет работать в сфере IT.
Абстрактное, критическое и стратегическое мышление, аналитические способности, умение выстраивать алгоритмы – «мастхэв» для хорошего разработчика.

ТОП 5 гибких навыков. Источник: amazonaws.com
Результативные занятия математикой придают уверенность в себе, ведь успехи в ней требуют упорства в стремлении решить самые сложные, иногда, на первый взгляд, «неразрешимые» задачи и проблемы.
Проверьте свои силы: Математические головоломки вам в помощь: 9 отборных известных задач на сообразительность. Сколько сможете решить? 8. Решение задач вырабатывает психологическую стойкость
Решение математических задач помогает улучшить эмоциональный фон – это занятие способно избавить от тревоги, помогает контролировать эмоции и предупреждает стресс.
К таким выводам пришли ученые из Университета Дьюка в США, которые сумели доказать это в исследовании, опубликованном в журнале «Клиническая психология» в 2016 году.
9. Удовольствие от «икс»
Для человека, серьёзно занимающегося математикой, математические формулы, уравнения и другие логические и математические задачи воплощают собой красоту, гармонию и доставляют такое же эстетическое удовольствие, как музыка, искусство и хорошая шутка, утверждает группа исследователей из нескольких университетов Великобритании.
С помощью функциональной магнитно-резонансной томографии была зафиксирована активность мозговой деятельности испытуемых во время демонстрации им математических уравнений, формул и задач. Результаты исследования опубликованы в журнале «Границы человеческой нейробиологии» (Frontiers in Human Neuroscience) в 2014 году.
Как научиться испытывать радость и наслаждение от занятий математикой рассказывает известный американский математик, выпускник Гарвардского университета, Стивен Строгац. Преподаватель прикладной математики, обладатель наград в области математики и преподавания на страницах своей книги «Удовольствие от X» с энтузиазмом, просто и понятно объясняет самые значительные математические идеи.
Мы убеждены, что детям, особенно в возрасте 5-9 лет, не обязательно рассказывать, как важно изучать математику. Гораздо важнее дать возможность ребёнку окунуться в мир занимательной интерактивной математики.

Обучаясь с помощью LogicLike, дети решают интересные логические задачи, зарабатывают за правильные ответы свои первые награды-«звезды», играют в современные логические игры – и получают не только пользу, но и настоящее удовольствие от такой математики.
logiclike.com
Роль моделирования при работе над задачей в 5 классе
ГОУ СПО «Кунгурское педагогическое училище»
Роль моделирования при работе над задачей в 5 классе
Курсовая работа по методике математики
Власовой Ольги Сергеевны
специальность: 050201 математика
группа: М – 41 отделение: очное
Руководитель: Т.А. Трясцына
преподаватель методики математики
Защита состоялась:
Отметка:
2007
Введение.......................................................................................................... 3
Теоретические основы моделирования.......................................................... 5
Понятие модели и моделирования.............................................................. 5
Моделирование в решении текстовых задач............................................... 10
Задачи на встречное движение двух тел................................................... 17
Задачи на движение двух тел в одном направлении................................ 17
Задачи на движение двух тел в противоположных направлениях.......... 18
Использование моделирования при работе над задачами на движение в 5 классе........................................................................................................................ 21
Заключение.................................................................................................... 39
Список литературы....................................................................................... 40
Приложение 1................................................................................................ 42
Решению текстовых задач отводится достаточно много времени в курсе математики. В ходе работы над задачами педагог раскрывает связи между данными и искомыми величинами, отношения, заданные в условии.
Учебная деятельность при решении задач складывается из умственных действий и осуществляется эффективно, если первоначально она происходит на основе внешних материальных действий с предметами, а затем превращается во внутренние процессы.
Таким образом, действия первоначально целенаправленно отрабатываются в плане внешних операций с вещами, а затем эти действия только представляются и проговариваются и, наконец, действия сворачиваются и уходят во внутренний план.
Как правило, в процессе анализа задачи учитель, а, следовательно, и ученики используют лишь различные виды краткой записи задачи или готовые схемы. Создание модели на глазах у детей или самими учащимися в процессе решения задачи считается очень важным.
«Рисунки, схемы, чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать наиболее рациональные пути решения задач, помогают не только усваивать знания, но и овладевать умением применять их. Эти условия необходимы для того, чтобы обучение носило развивающий характер.»[10, 7]
Графические изображения, используемые для постановки познавательных задач, наглядно представляя соотношения между данными и искомыми величинами, помогают ученикам схватить смысл проблемной ситуации, а затем и найти возможный путь решения.
Главное для каждого ученика на этом этапе – понять задачу, то есть уяснить, о чем эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми параметрами. Для этого следует применять моделирование и учить этому детей.
Целью данной курсовой работы является разработка системы приемов моделирования.
Задачи:
1) познакомиться с понятиями «модель» и «моделирование»;
2) рассмотреть разные виды моделей, включить их в практическую работу с детьми;
3) изучить теоретические, методические источники по данному вопросу;
4) систематизировать приемы моделирования;
5) разработать конспекты уроков математики, провести и проанализировать их.
Объект исследования: учебная деятельность пятиклассников на уроках математики.
Предмет: процесс формирования у пятиклассников умений решать текстовые задачи, используя модели.
Контингент: учащиеся 5 классов лицея № 1 города Кунгура.
Гипотеза данной курсовой работы: использование моделирования влияет на формирование умения решать задачи.
Обучение математике требует развития у детей самостоятельности в решении текстовых задач. Каждый ученик должен уметь кратко записывать условие задачи, иллюстрируя ее с помощью рисунка, схемы, чертежа и других видов моделей, обосновывать каждый шаг в анализе задачи и ее решении, проверять правильность решения.
Таким образом, моделирование – это один из ведущих методов обучения решению задач и важное средство познания действительности.
Понятие модели и моделирования
В науке широко используется метод моделирования. Он заключается в том, что для исследования какого-либо объекта или явления выбирают или строят другой объект, в каком-то отношении, подобный исследуемому. Построенный или выбранный объект изучают и с его помощью решают исследование задачи, а затем результаты решения этих задач переносят на первоначальные явления или объект.
Под моделью (от лат. modulus – мера, образец, норма) понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект – оригинал, сохраняя некоторые важные для данного исследования типичные черты. Процесс построения и использования модели, называется моделированием.
Во всех науках модели выступают, как мощное орудие познания.
Например:
1. Люди издавна интересуются, как устроена наша Вселенная. Этот интерес не только познавательный, но и сугубо практический, так как люди хотели научиться предсказывать периодические явления, связанные с устройством Вселенной, такие, как: затмение солнца и луны, наступление времен года.
Для решения этих задач, ученые строили свои представления о Вселенной в виде схемы картины мира, в которой объекты планеты солнце и звезды, планеты, земля и луна изображались точками, движущимся по каким-то кривым – траекториям их движения. Таковы, например, схемы, построенные Птолемеем, в которых центральное место занимала наша Земля, или схема Коперника, в которой центральное место занимало Солнце.
С помощью этих схем ученые решали задачи предсказания отдельных астрономических явлений. Эти схемы или картины мира – суть модели Вселенной, а метод исследования Вселенной, нахождение законов и решения задач, связанных с помощью этих моделей, является методом моделирования.
2. Люди издавна интересуются, как устроены они сами, как функционирует человеческий организм. Но исследовать эти вопросы на живом человеческом организме очень трудно. Ибо такое изучение до появления особых приборов было связано с гибелью этого организма. Тогда ученые стали исследовать устройство человеческого организма на подобных его организму животных. Изучение организма животных, их функционирование помогло установить многие важнейшие закономерности функционирования человеческого организма.
В этих исследованиях организмы животных выступали в качестве модели человеческого организма, а при этом метод есть моделирования.
В математике широко используется метод моделирования при решении задач.
Математической моделью можно назвать специальное описание (часто приближенное) некоторой проблемы, ситуации, которое дает возможность в процессе ее анализа применять формально – логический аппарат математики. При математическом моделировании имеем дело с теоретической копией, которая в математической форме выражает основные закономерности, свойства изучаемого объекта.
В процессе математического моделирования выделяют три этапа:
1. Формализация – перевод предложенной задачи (ситуации) на язык математической теории (построение математической модели задачи).
2. Решение задачи в рамках математической теории (говорят: решение внутри модели).
3.Перевод результата математического решения задачи на тот язык, на котором была сформулирована исходная задача (интерпретация решения).
Чаще всего математическая модель представляет собой несколько упрощенную схему (описание) оригинала, а значит, обладает определенным уровнем погрешности.
Одна и та же модель может описывать различные процессы, объекты, поэтому результаты внутримодельного исследования одного явления зачастую могут быть перенесены на другое. В этом состоит одно из основных достоинств математического моделирования.
Математика не только создала разнообразные внутренние модели алгебры, геометрии, функции комплексного переменного, дифференциальных уравнений и т.д., но и помогла естествознанию построить математические модели механики, электродинамики, термодинамики, химической кинетики, микромира, пространства – времени и тяготения, вероятностей передачи сообщений, управления, логического вывода.
Созданием моделей математика часто опережала потребности естествознания и техники.
Реализация универсального математического метода познания есть основная цель и задача современной математики. Она включает, в первую очередь, построение новых, неведомых математических моделей, в частности в биологии, для познания жизни и деятельности мозга, микромира, новых, фантастических технологий и техники, а также познание экономических и социальных явлений также с помощью математических моделей различными математическими методами. [Приложение 1]
Любая математическая задача состоит из условия (утверждения), вопроса или требования. Причем, в задаче обычно не одно, а несколько элементарных условий. Они представляют собой количественные или качественные характеристики объектов задачи и отношения между ними.
Требований в заданиях тоже может быть несколько. Они могут быть сформулированы, как в вопросительной, так и в утвердительной форме. Условия и требования взаимосвязаны. Систему взаимосвязанных условий и требований называют высказывательной моделью (словесной).
mirznanii.com
 Многочисленные опросы учащихся, проведенные нами и другими исследователями, показали, что учащиеся этого не знают. На вопрос: «Что такое модель?» — они дают самые невразумительные ответы или вообще ничего сказать не могут, а в качестве примеров моделей указывают лишь на модели геометрических тел, стоящие в шкафах математического кабинета. На вопрос: «Приведите примеры математических моделей» — учащиеся опять-таки ссылаются на указанные модели геометрических тел, хотя в самом деле они ими не являются.
Многочисленные опросы учащихся, проведенные нами и другими исследователями, показали, что учащиеся этого не знают. На вопрос: «Что такое модель?» — они дают самые невразумительные ответы или вообще ничего сказать не могут, а в качестве примеров моделей указывают лишь на модели геометрических тел, стоящие в шкафах математического кабинета. На вопрос: «Приведите примеры математических моделей» — учащиеся опять-таки ссылаются на указанные модели геометрических тел, хотя в самом деле они ими не являются. Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда: 












