Муниципальное автономное дошкольное образовательное учреждение

комбинированного вида города Тюмени

Как наконец перестать бояться математики и научить этому ребёнка. Как научить ребенка математике 8 класс

Особенности изучения математики в 8 классе. " Такая , совсем не страшная математика "

Особенности изучения математики в 8 классе.

(выступление на родительском собрании 8 классов 10.09.2015. Шиленковой Е.В.)

Такая , совсем не страшная математика

Сколько всяких ничем не обоснованных страхов и предубеждений сыпется на бедную математику, а ведь нет более труднопреодолимого препятствия, чем накрепко засевшие в нашей голове предрассудки.

В действительности существует совсем немного людей, наделённых математическими способностями от природы, все же остальные преуспевают в этой науке благодаря добросовестной и настойчивой учёбе. «Без труда не выловишь и рыбку из пруда» - эта мудрость не обходит стороной и математику.

Курс алгебры в 8 классе построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований.

Одной из главных особенностей курса алгебры является то, что в нем реализуется взаимосвязь принципов научности и доступности и уделяется особое внимание обеспечению прочного усвоения основ математических знаний всеми учащимися.

Особенностью курса является также его практическая направленность, которая служит стимулом развития у учащихся интереса к алгебре, а также основной для формирования осознанных математических навыков и умений.

«Идеология» основного курса алгебры делает его органическим продолжением и обобщением курса арифметики. Центральное понятие этого курса – понятие числа – развивается и расширяется от рационального до действительного.

Усвоение алгебры осуществляется успешно, если изучение теоретического материала проходит в процессе решения задач. Этим достигается осмысленность и прочность знаний учащихся.

Большое количество разнообразных задач на применение алгебры в геометрии, физике, технике и т.д. помогает учащимся понять практическую необходимость изучения алгебры.

В ходе освоения содержания курса учащиеся получают возможность:

развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Изучение алгебры в 8 классе направлено на достижение следующих целей:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Общеучебные умения, навыки и способы деятельности.

В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевалиумениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

В курсе алгебры 8 класса систематизируются знания обучающихся о числовых выражениях; вводятся понятия: неравенство, система неравенств, арифметический квадратный корень, квадратное уравнение и неравенство, квадратичная функция. Вырабатываются умения:

выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
решать линейные неравенства с одной переменной и их системы;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики.

Место предмета

В соответствии с учебным планом школы в 8 классе отводится 3 часа в неделю для обязательного изучения алгебры. В рабочей программе предусмотрен резерв свободного учебного времени в объеме 3 часов.

Результаты обучения

Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достичь все учащиеся, оканчивающие 8 класс, и достижение которых является обязательным условием положительной аттестации ученика за курс 8 класса.

А теперь, специально для родителей!

Общие советы по изучению математики. Работа по изучению математики должна быть систематической, ежедневной, без каких-либо перерывов, за исключением, конечно, дней отдыха.

1. Надо стремиться к тому, чтобы сразу понять все, что изучается

на уроках.

Надо освоить все действия, все умения, которые отрабатываются на уроках.
Надо стараться «докапываться» до главного, до общих основ изучаемого материала.
Надо приучать себя к постоянному самоконтролю и самооценке своей учебной работы.

Советы по работе с учебником математики. 1.Прочитать содержание пункта (параграфа). 2.Выделить все непонятные слова и выражения, выяснить их значение (в учебнике, справочнике, у учителя, родителей, товарищей). 3.Задать по ходу чтения вопросы и ответить на них.

О чем здесь говорится?
Что мне уже известно об этом?
Что именно об этом сообщается?
Чем это можно объяснить?
Как это соотносится с тем, что я уже знаю?
К чему, когда и как это можно применить?

4.Выделить и изучить основные понятия или правила. 5.Разобрать конкретные примеры в тексте и придумать свои. 6.Запомнить материал, используя приемы запоминания (пересказ по плану, чертежу, схеме, мнемонические правила, повторение трудных мест). .

Советы по выполнению письменной домашней работы.1.Прочитать задания, изучить их. 2.Продумать, какие правила и приемы следует применить для их выполнения, пользуясь, если нужно, предыдущей письменной работой, общими и частными приемами решения задач. 3.Если нужно, выполнить задание полностью на черновике или частично. 4.Проверить тем или иным способом решение задачи. 5.Записать выполненные задания в тетрадь, соблюдая правила ведения тетради по математике.

Что делать если не получается решить задачу? 1.Проверить правильность записи условия. 2.Проверить ход решения, правильно ли использован прием решения. 3.Проверить правильность записей и чертежей. 4.Проверить вычисления. 5.Исследовать решение, рассмотрев частные случаи. 6.Рассказать кратко ход решения задачи. 7.Полезно обсудить решение с товарищем.

Как работать с теоремой.

1.Прочитать теорему(по учебнику,тетради)

2.Рассмотреть (если есть) чертеж, усвоить его.

3.Прочитать доказательство,обосновывая каждый этап,следя по чертежу.

4.Повторить и выучить доказательство.

5.Сделать свой чертеж и с его помощью доказать теорему самостоятельно.

6.Проверить себя,прочитав доказательство еще раз.

7.Попробовать найти другой способ доказательства.

Уважаемые родители!

Если вы хотите, чтобы у ваших детей не было проблем с математикой, то сформулируйте для них десять полезных советов и следите, чтобы они придерживались их.

Десять полезных советов (для учеников)

Совет 1: настройтесь на успех!

Если ты достаточно успешно справляешься с другими школьными дисциплинами, ты просто не можешь не справиться с математикой – это только дело времени и твоего собственного труда. При изучении математики используются те же логические построения, что и в остальных науках.

Совет 2: постоянно тренируйтесь!

Окружающий нас мир полон множеством чисел, которыми мы постоянно пользуемся. Почему бы не попробовать использовать их для тренировки наших математических способностей и начать складывать числа на номерах проезжающих мимо машин, считать количество шагов до школы, магазина и узнавать скорость вашего движения до этих пунктов?

Совет 3: воспринимайте математические примеры как игру!

Самый сложный и страшный пример попробуйте превратить в игру, а все возможные варианты его решения, пусть даже сначала ошибочные, воспринимайте как захватывающую погоню за кладом. Никаких пробелов в знаниях быть не должно, все пройденные правила и теоремы надо знать наизусть – именно они основа всего, без них не обойтись так же, как и без знания карты местности, где зарыт клад.

Совет 4: необходимо хорошо понимать смысл правил и теорем!

Вы не сдвинетесь с места, если будете просто зазубривать все теоремы. Необходимо очень хорошо представлять себе, о чем именно в них идет речь. Вам мало поможет тот факт, что "квадрат гипотенузы равен сумме квадратов катетов”, если вы не представляете, что такое катет и где он находится.

Во время объяснения учителем нового материала не стесняйтесь спрашивать сразу, что непонятно, поскольку именно для этого учитель и находится в классе.

Совет 5: создайте себе окружение из формул!

Окружи себя формулами, которые тебе необходимо выучить. Напиши их на листе бумаги и повесь в своей комнате или около зеркала. Постоянно натыкаясь на них, ты запомнишь их как навязчивую телевизионную рекламу и, в случае надобности, всегда сможешь вызвать их в памяти.

Совет 6: не ломайте голову в одиночестве!

Длинные тоскливые примеры и сложнейшие задачи прямо-таки преображаются, оживают, если к их решению приступить в компании с другом или подругой. Обмениваясь каждый своим вариантом решения, легче и веселее идти к истинному ответу.

Совет 7: внимательно читайте задание!

Очень часто ключ к решению задачи таится в ее условии, и все ваши неудачи из-за того, что вы невнимательно прочитали задание. Внимательно и вдумчиво прочитайте задание и только потом приступайте к его решению.

Совет 8: действуйте методически!

Прежде всего, исходите из данных, имеющихся в вашем распоряжении, изобразите их все при помощи таблицы или чертежей на листе бумаги для наглядности. Воспроизведите в памяти и напишите все теоремы или правила, вам известные и имеющие отношение к данному вопросу.

Совет 9: постоянно контролируйте свои действия!

Каждый раз проверяйте произведенные математические операции, чтобы в них не закралась какая-нибудь неточность, которая потом повлияет на правильность окончательного решения. Также не забывайте проверять, все ли исходные данные были вами задействованы – они не могут остаться невостребованными в решении задания.

Совет 10: наведите порядок в цифрах!

Математика – наука точная, и, как ни одна другая не терпит даже малейших неточностей. Сколько уже вы наделали ошибок из-за неправильно прочитанного числа, лишнего нуля или если пишете «как курица лапой».

Итак, если хотите подружиться с математикой, вам придется стать точным и последовательным, не оставлять без внимания даже такие мелочи, как промежутки между цифрами, ровные и аккуратные столбики вычитания и сложения, а также количество таких любителей теряться, как нолики.

Дорогие мамы и папы!

Всегда помогайте своим детям, тогда в будущем и вы сможете рассчитывать на их помощь.

Удачи и успехов в изучении математики!!!

infourok.ru

Как репетитор по математике мотивирует ученика в 8 классе

Для того, чтобы школьные оценки по математике радовали репетитора и родителей, а ребенок шел на индивидуальный урок как на праздник, необходимо продумать мотивационную стратегию занятий. Дети устают от ежедневного монотонного общения с числами, формулами, переменными, графиками. Поэтому если репетитор по математике не использует на уроках никаких практических заданий на применение получаемых знаний – поддерживать интерес к математике будет очень сложно. В 5 – 6 классе репетитору помогает естественная япотребность ребенка к познанию окружающего мира и изучению простых арифметических действий, необходимых каждому человеку в реальной жизни. Тут и проценты, без которых трудно представить себе современную торговлю (скидки, удешевления, подорожания) и единицы измерения, встречающиеся практике сплошь и рядом.

В 7 классе школьная математика в сочетании репетитором, как правило, утомляет ученика, ибо нагрузка растает, а использование получаемые знаний становится менее очевидным. Новые понятия и теоремы, о которых твердит репетитор по математике на каждом уроек, казалось бы, нужно знать только для получения хорошей оценки. От чисел, степеней, одночленов, многочленов, графиков, скобок и модулей только голова болит вечерами. Ребенку трудно целенаправленно заниматься, так как он не видит применения законов математики, изучаемых в 7 классе. Однако уже к 8 классу, когда репетитор по математике вплотную подходит к теореме Пифагора и квадратным уравнениям, мотивационный рычаг снова приобретается и в умелых руках грамотного преподавателя оказывает еще большее воздействие на сознание ребенка. Рассмотрим один из самых эффектных и мощных мотивационных ходов репетитора по математике — задача на измерение глубины озера. Она может быть рассмотрена репетитором в самых сложных случаях пониженного интереса ученика к предмету. Как в целом к математике, так и к геометрии в частности.

Итак, репетитор описывает своему ученику реальную ситуацию. Рыбак плывет по озеру на лодке. Чтобы определиться с местом ловли нужно понять, какова глубина водоема в данной точке. Как назло у рыбака нет под рукой никаких измерительных приборов, кроме небольшой рулетки или предмета известной длины. Рядом с лодкой из воды торчат два тростника, по всем признакам растущие от одного корня со дна водоема. Как измерить глубину озера?

Простое и понятное условие задачи позволяет репетитору по математике полностью овладеть вниманием своего подопечного. Ученик моментально включается в обсуждение проблемы и пытается самостоятельно искать решение, напрягая мозги «по полной программе». После очередной попытки ответить правильно и осознания своей неспособности догадаться до хитрого метода, он просит у репетитора подсказку. Преподаватель берет чистый листочек и строит несложную математическую модель задачи: озеро в разрезе. Сделаем это и мы. Пусть отрезок АВ – изображает тростник. В – его корень на дне водоема. Точка С – находится на поверхности воды.

Для того, чтобы показать реальную модель ситуации репетитор по математике кладет на лист бумаги парочку стержней, имитирующих ствол тростника и поворачивает один из них вокруг точку В до того момента, пока его конец (точка А) не попадет на прямую a — имитирующую поверхность воды. Слова репетитора по математике могут быть следующими: «Рыбак выравнивает стволы тростника (обрезая лишнее в случае необходимости), а затем отгибает один из них момента, пока макушка не поравняется с поверхностью воды». Далее на рисунке репетитор по математике отмечает точку H на прямой а: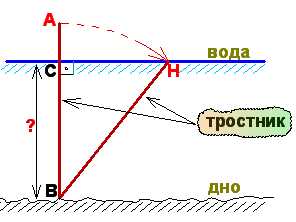

так, что BH=AB и соединяет H и B отрезков. Понятно, что все расстояния над поверхностью воды можно измерить, поэтому можно считаь, мы нам известны длины AC и CH. Если СН окажется слишком большим для измерения СН, то для того, чтобы не перемещать лодку, рыбаку следует обрезать макушки тростника до удобной длины и, соответственно, до удобного расстояния от СН. Это же самое делает репетитор по математике. Итак, пусть AC=a; CH=b и CB=x. Тогда BH=x+a в треугольнике CBH все стороны оказываются выраженными через числа a; b и икс. Пр помощи этих буквенных выражений и простенького квадратно-линейного уроавнения репетитор по математике находит глубину озера.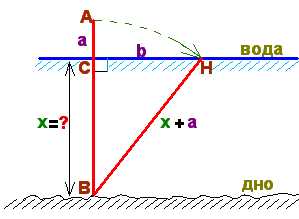 Подставляя их в теорему Пифагора для треугольника CBH, получаем цепочку равенств:

В конечно итоге репетитору по математике удается связать глубину озера с длинами отрезков: высоты торчащих над водой частей тростника и длины отклонения макушки до погружения в воду. Ровно так же может поступить и рыбак, владеющий искусством составления уравнений.

После таких демонстраций ученик начинает понимать, зачем ему надо учить математику и ходить к репетитору. В школе практическому применению знаний почти не учат, поэтому возникает потребность в индивидуальных занятиях у репетитора.

Практическая актуальность рассмотренной задачи, ее ненадуманная форма и красивое решение воспитывает подлинный интерес к математике, как к очень интересному и важному предмету, а использование приобретенных знаний стимулирует их дальнейшее накопление.

Репетитор по математике – Москва, Строгино, Колпаков А.Н.

Метки: Занимательный репетитор по математике, Мотивация обучения, Работа репетитора, Репетиторам по математике, Ученикам

ankolpakov.ru

Как научить малыша считать?

Из всех методов раннего развития, подход Глена Домана к обучению математике является наверное самым … удивительным. Мы привыкли к тому, что сначала нас обучают последовательности чисел (1, 2, 3, 4 …), потом простым арифметическим подсчетам с помощью пальцев и счетных палочек, период же перехода к настоящей «взрослой математике» — это долгий и затруднительный процесс для каждого малыша, включающий в себя сначала отлучение от счета пальцами к произведению математических действий в голове, который проходит, как мы все знаем, со значительными усилиями для наших детей.

Глен Доман считает, что нет никакой необходимости так долго мучить детей всеми этими счетами на пальцах и палочках. По данным исследования, проведенных в его институте «Достижения человеческого потенциала», дети рождаются уже со способность различать количество объектов. Глядя на сотни точек, они могут с точностью определять их количество без особых усилий и при этом очень быстро — достаточно всего лишь одного их мимолетного взгляда. Научно доказано, что такая особенность человеческого организма по статистике сохраняется от 0 до 3 лет. И на это способен каждый ребенок, главная же задача родителей помочь развить в нем эти способности. Для того чтобы это сделать, Глен Доман предлагает использовать большие карточки с красными точками от 0 до 100 точек. Ежедневно нужно показывать малышу 10 карточек с набором случайных точек. Работая с этими материалами, малыш может освоить не только количества, но и арифметические действия: сложение, вычитание, умножение, деление, а также дроби, последовательности, сложные примеры, в общем все то что дети проходят в школе с первого по 9 класс. Вашим малышам не нужны никакие формулы для решения примеров, они сходу смогут решать очень сложные примеры, прямо как компьютер или «маленький калькулятор»))

Например, 127 +12-66 * 2 = …

Вы сами не можете посчитать этот пример, а Ваш малыш сможет в одну секунду, если с ним заниматься математикой по методике Глена Домана…

Действительно ли это работает?

Изучая иностранные и русские форумы в интернете, я столкнулась с опытом мам уже давно занимающихся по этой методике раннего развития. И вот что я узнала, малыш способен различать количества точек только в период с 0 до 3 лет, потом эта способность уходит. А дело все вот в чем.

Дело в том что период от 0 до 3 — это период, когда правое полушарие мозга человека доминирует над левым полушарием, соответственно, эта способность, как правило, у всех детей уходит после 3 лет.

Поэтому возникает главный вопрос: «А стоит ли вообще заниматься и тратить столько времени на изучение карточек с красными точками, если все равно после 3 лет ребенок не сможет воспринимать их?»

Мое личное мнение таково, что, как и любая система обучения, все зависит от конкретного ребенка и, конечно, родителей. Огромное количество детей уже прошли через всю программу, правда, без удивительных результатов. Каждому свое, как говориться, но я уверена, что время прошло не зря, дети, прошедшие эту программу раннего развития, безусловно, гораздо более развитые и сообразительные, чем их сверстники. Кроме того, кто знает, может быть эти знания выплывут на поверхность в будущем. Кроме того, мне кажется, если грамотно подходить к этой методике, то можно как раз до трех лет мягко совершить переход от карточек с количествами точек на карточки с цифрам и продолжить обучение уже с ними.

Я со своей доченькой Стефанией занимаюсь математикой с 1 года и 2 месяцев. Сейчас ей 1 год и 4 месяца и я уже вижу просто колоссальные результаты. Она уже может решать несложные примеры и показывать простые количества. Так что посмотрим, что будет дальше. Продолжаем заниматься.

В интернете есть примеры людей, которые сумели сохранить эту удивительную способность отличать сколько красных точек на карточке за несколько секунд, сколько, например, виноградинок лежит на тарелке, сколько спичек в коробочке…и после 3 лет. Так почему бы не помочь нашим детям насладиться этой удивительной наукой математикой с самого рождения, тем более что малыши хотят все знать..?! Давайте же им поможем в этом:))

Основные правила

Начинайте как можно раньше.
Будьте в хорошем настроении в любое время.
Уважайте вашего ребенка.
Начинайте заниматься с малышом только тогда, когда Вы оба находитесь в хорошем расположении духа.
Остановитесь, до того момента, как Ваш малыш захочет остановиться.
Показывайте карточки как можно быстрее.
Добавляйте новый материал как можно больше.
Соблюдайте последовательность занятий.
Заранее готовьте материал.
Помните основной закон:Если Вы или ваш малыш не хочет заниматься математикой, значит Вы что-то делаете неправильно.

Этапы обучения

Нулевой этап (для новорожденных — дети в возрасте до 3 месяцев, все остальные дети должны начинаться с первого этапа) — нам понадобятся карточки с точками очень большого размера: 15 x15″, с красными, очень жирными точками 1,5 см в диаметре. Начните с одной карточки, покажите ее в течение 10-15 секунд, удерживая ее перед глазами малыша, чтобы дать ему возможность сосредоточиться на ней. Первый день показываем карточку с одной точкой в течение 10 раз, на второй день карточку с двумя точками в течение 10 раз; таким образом, в течение 7 дней показываем малышу карточки от 1 до 7 в течение 10 раз ежедневно. Повторите эти действия в течение следующих двух недель: так, за первые три недели вы показываете карточку с одной точкой по понедельникам, с двумя точками по вторникам и так далее … На 4-й неделе: берем карточки от 8-14 точек и и начинаем их показывать таким же образом, то есть 10 раз в день. Таким образом, у нас получается следующая схема — следующие три недели мы показываем карточку с восемью точками по понедельникам, карточку с девятью точками по вторникам, и т.д.), далее вводим следующий набор карточек и показываем аналогичным образом. При показах карточек обратите внимание на следующий важный момент! Выберите правильное время дня: когда ребенок находится в хорошем настроении.

Как только вы поймете, что ваш малыш видит точки на карточках ясно и четко, переходите к первому этапу.

Первый этап — КоличествоОбучение малыша происходит следующим образом — ежедневно нужно показывать малышу 2 набора по 5 карточек 3 раза в день. Каждый раз карточки нужно перемешивать. На следующий день добавляем к набору следующие 2 карточки и вынимаем из набора 2 самые старые карточки. Таким образом, показываем карточки-точки количества от 0 до 100.
Второй этап — УравненияНачинаем показывать после того, как показали первые 20 карточек из первого шага.Занятие должны происходить следующим образом, ежедневно нужно показывать малышу 3 примера на сложение 3 раза в день, при этом продолжаем вводить новые карточки количества, которые также продолжаем показывать 2 комплекта по 5 карточек 3 раза в день, пока не дойдем до 100. Уравнения на сложение должны быть простыми, но непредсказуемыми , например, 2 +2 = 4, 5 +11 = 16. Избегайте следующих уравнений: 0 +1 = 2, 1 +2 = 3; 2 +2 = 4. Уравнения на сложение показывайте в течение 2 недель, затем перейдите к вычитанию, через еще 2 недели приступите к умножению, а потом к делению.
Третий этап — Уравнения в несколько действийК третьему этапу Вы можете приступить, когда Вы Вы полностью завершите первый этап (пройдете количества от 0 до 100) и второй этапа (простые уравнения).Начинайте работать с уравнениями в три действия, например: 3+4+7 = 14.Параллельно Вы можете попробовать протестировать Вашего малыша. Это можно сделать следующим образом.
- Держите две карточки перед лицом малыша и громко и весело спросите, где 5. При этом показывайте 2 карточки на выбор, например, карточки 5 и 10. Промежуток между количествами первоначально делайте хотя 5 цифр. Если Ваш малыш покажет правильно, то обязательно бурно похвалите его, если нет, то ни в коем случае не ругайте его, а спокойно скажите и покажите, где 5, а где 10.
- Второй тип проверки. Это проверка уравнений, дайте малышу решить простое уравнение, произнесите его вслух и покажите 2 варианта ответа, чтобы он выбрал результат. Если Ваш малыш не хочет отвечать и игнорирует Вас просто и весело произнесите правильный ответ, если ответит правильно бурно и радостно похвалите его, если неправильно спокойно исправьте его.
После нескольких недель показа уравнений в несколько одинаковых действий объедините сложение и вычитание, умножение и деление, но не смешивайте их, например, 10 +5-3 = 12, а не 3 +4 * 6=27После нескольких недель такого показа, добавляем еще одно действие для уравнений: 45 +11-3-6 = 47.В качестве дальнейших ступеней Вы можете ввести также:
1. Последовательности
2. Больше и меньше
3. Равенства и неравенства
4. Простую алгебру и другое.
Четвертый шаг — Переход на цифрыКарточки с цифрами должны быть размером 11 ? 11, написанные черным шрифтом.На этом этапе показываете малышу карточку с точками и эквивалентную ей карточку с цифрами.
Пятый шаг — Уравнений с цифрамиНа этом этапе начинаем показывать аналогично способу с точками уравнения с цифрами.

Полезные материалы и ресурсы

Я думаю, что для каждой мамы будет затруднительно изготавливать такое огромное количество карточек с точками, поэтому есть неплохие альтернативы. На мой взгляд, очень хорошие карточки разработаны компанией Умница Маниченко по методу Глена Домана.

Этот комплект называется Математика с пеленок. Его можно купить на официальном сайте компании. Сайт компании www.umnitsa.ru

Стоимость такого комплекта 1925 руб на сегодняшний день.

Почитать подробнее об этом наборе и моем опыте обучения дочери по нему можно будет здесь.

2). Здесь можно скачать бесплатно программу по обучению математике с пеленок.

Кстати, очень хорошая программа, написана самими родителями для своих малышей. Ее можно совмещать с карточками. Но все-таки, по моему опыту я советую начать с самих карточек, а потом, когда Вы пройдете количества хотя бы до 20 можно дополнять этой компьютерной программой. Если же начать обучать по этой программе малыш может потом отказаться смотреть простые карточки. Так что будьте осторожны с компьютером.

3). Вот еще одна бесплатная программа по обучению математике для малышей

4). Здесь можно скачать бесплатно много презентаций по математике

Как понять алгебру: мыслим логически

Алгебра – это наука, с которой люди знакомятся, учась в средней школе. Ученики, которые понимают этот предмет, считают, что ничего сложного в нем нет. Однако есть ребята, которые совсем не могут вникнуть в суть науки. У них падает самооценка. Наиболее распространенный вопрос таких школьников звучит примерно так: «Как понять алгебру, если ты тупой?». Поверьте, вникнуть во все формулы и задачи под силу каждому человеку. Дело состоит в выборе методики изучения и профессионализме преподавателя.

Главное – это правильная постановка цели. Вы должны осознать, до какой степени вы желаете вникнуть в науку. После постановки соответствующих задач начинайте воплощать мысли в реальность.

Советы для самостоятельного изучения алгебры

Если вы решили самостоятельно изучить алгебру, то воспользуйтесь этими простыми, но эффективными советами:

Прежде чем начинать решение задач, узнайте, что означает каждый незнакомый вам термин и понятие. Так вы сможете наиболее правильно понять суть задания, а это, как говорят преподаватели, уже половина решения.
Когда вы будете изучать методы алгебры, сразу же решайте задачу, которая относится к конкретной теме. Так вам не придется заучивать теорию, вы на практике вникнете в суть проблемы.
После изучения определенной темы постарайтесь объяснить другому человеку ее суть. Так вы закрепите полученные знания.

Если самостоятельное обучение вам не по силам, то вы всегда можете воспользоваться услугами репетитора.

Занятия с репетитором

Если вы так и не смогли самостоятельно поработать и не знаете, что делать, если не понимаешь алгебру, то помощь профессионального педагога будет очень к месту. Положительных моментов в таких уроках очень много. Вот некоторые из них:

Вам не придется выбирать методику обучения.
Гораздо проще бороться с ленью, если за каждое занятие вы платите деньги.
Преподаватель сможет контролировать уровень ваших знаний.
Если определенная тема вам не станет понятна, то репетитор будет объяснять ее столько раз, сколько потребуется.

Вопросов о том, как понять алгебру, занимаясь с преподавателем, возникать не будет. Грамотный педагог подберет необходимую методику и поможет освоить самые трудные темы. Главное условие – это ваше желание, поскольку ни одного человека нельзя чему-то научить, если он сам этого не захочет.

Как понять алгебру с нуля

Если вы изначально не понимаете эту науку, то очень трудно будет никнуть в ее суть в дальнейшем. В алгебре все взаимосвязано. Сложные темы строятся на основании более простых. Поэтому бесполезно изучать математику 9 класса, если вы не освоили азы. Не важно, какой способ обучения вы выбрали. Самостоятельно или с репетитором начинайте проходить самые первые, вводные темы, решайте простые задачки. Люди, которые разбираются в алгебре, с уверенностью говорят, что если учиться постепенно, то никаких трудностей не возникает.

Чтобы облегчить процесс освоения науки, воспользуйтесь полезными советами, которые помогут вам подобрать для себя правильную мотивацию.

Полезные советы

Если вы уже определились для себя, как понять алгебру, но все равно эта наука дается вам крайне сложно, и вы не желаете ее изучать, воспользуйтесь этими советами:

Практически все ученики терпеть не могут домашнюю работу. Поймите, что она нужна, чтобы вы лучше запомнили материал, чтобы он отложился у вас в подсознании. Всемирно известные психологи уверяют, что повторенная информация усваивается нашим мозгом гораздо лучше.
Даже если вы поняли тему, порешайте задачи. Практической части обучения не заменит даже идеально изученная теория.
Если на занятии вы не поняли материал, не стесняйтесь сказать об этом преподавателю. Обычно учителя доброжелательно относятся к школьникам, которые стараются вникнуть в суть.
Не ограничивайте себя школьным учебником. Информацию можно узнать из разных источников, пользуйтесь этим. Это поможет вам всесторонне взглянуть на эту науку и лучше ее понять.

К данным советам стоит обращаться, если вы настроены на реальный результат и понимаете, что лень придется отложить в далекий ящик. Чтобы понять, что вас ожидает в процессе обучения, узнайте мнение людей, которые уже освоили эту науку.

Мнение людей, знающих алгебру

Люди, которые уже прошли все стадии обучения, дают школьникам, желающим постичь суть алгебры, такие советы:

Занятия с репетитором дают гораздо более качественный результат, чем самостоятельные.
Выучить алгебру за полгода возможно, но вам придется каждый день сидеть за учебниками.
Консультации с людьми, которые знают математику – обязательная составляющая обучения.
Без соответствующей мотивации вам не обойтись.
Изучать алгебру с середины курса нельзя. Нужно начинать с азов.

Таким образом, изучить алгебру – вполне посильная задача. Главное – верить в себя и быть настойчивым человеком.

fb.ru

Как наконец перестать бояться математики и научить этому ребёнка

Даже если вы не были фанатами математики в школе, помогать ребёнку с домашкой рано или поздно придётся. Математики Роб Истуэй и Майк Эскью написали книгу «Математика для мам и пап» о том, как просто и интересно объяснить ребёнку дроби, умножение, деление и даже проценты. С разрешения издательства «Альпина Паблишер» мы публикуем отрывок из книги.

Рассылка «Мела»

Мы отправляем нашу интересную и очень полезную рассылку два раза в неделю: во вторник и пятницу

Откуда берётся страх перед математикой

Все мы не раз слышали, будто существуют люди, лишенные «математического гена» (что, разумеется, подразумевает, что они также не в состоянии передать этот ген своим детям). Может быть, это объясняет «математикофобию»?

Ответ почти наверняка отрицательный, потому что такой штуки, как математический ген, не существует. Откуда бы ему взяться? Человечество занимается алгеброй, теорией вероятности и математическим анализом всего лишь несколько сотен лет. Сегодня большинство взрослых, даже тех, кто считает себя неспособным к математике, на самом деле гораздо более сведущи в ней, нежели все люди Средневековья, за исключением крохотной их доли, а на развитие генов уходят тысячи или даже миллионы лет. Таким образом, те качества мозга — какими бы они ни были, — которые позволяют одним людям блистать в математике, тогда как другие с трудом осваивают школьную программу, никак не могут быть связаны с геном, специально посвященным математике. (Ученые считают, что математические способности могли возникнуть у человека как побочный продукт языкового общения, требующего высокого уровня абстрактного мышления.)

Если поговорить с человеком о его нелюбви к математике, то в большинстве случаев услышишь рассказ об учителе или о ком-то из родителей, чье вмешательство и породило комплекс неполноценности. Люди боятся не математики как таковой; они боятся оказаться в неловкой ситуации, опасаются конфуза.

Когда понимаешь, сколько родителей, бабушек и дедушек имеют в своей копилке дурные воспоминания об уроках математики в прежние времена (а под прежними временами мы подразумеваем не только Вторую мировую, но и 1980-е годы тоже), испытываешь настоящий шок. Постоянно приходится слышать и истории о ритуальных унижениях перед всем классом. Кое-кто вспоминает наказания и физическую боль: «Перкинс, чему равно семью восемь?» «Э-э, пятьдесят четыре?» (После этого Перкинс поспешно ныряет под парту, а над его левым ухом проносится губка для стирания с доски.)

Некоторые испытывали скорее психологическое страдание. «В худших своих кошмарах я видела, как мистер Грегори стоит перед классом и заставляет нас скандировать „Математика — это здорово, математика — это здорово“», — рассказала одна мама. Она сказала также, что, если все время говорить людям, что какая-то вещь — это здорово, эффект может оказаться противоположным задуманному. Кроме того, будем реалистами. Все полезное, что стоит изучать, требует усилий, и математика не исключение.

Одна из серьёзнейших наших проблем — уверенность в том, что учёба должна доставлять только удовольствие и даваться без труда

В результате у детей создается впечатление, что если при изучении математики им приходится напрягаться, значит, они к математике не способны. В Японии, где традиции высоких стандартов в математике очень сильны, акцент, как правило, делают на старание и усердие, а не на способности.

Конечно, трудно выяснить, как часто люди на самом деле сталкиваются с такого рода ситуациями, вызывающими у них ночные кошмары, но иногда, вероятно, достаточно мгновенного унижения, чтобы стройное здание математики рухнуло. Многие родители помнят момент, когда этот школьный предмет вдруг превратилась для них в кирпичную стену, а дальнейший прогресс в данной области стал казаться невозможным. Такое может случиться и с хорошим математиком тоже, — разница в том, что они, как правило, утыкаются в свою стену в университете или еще позже. Многие математики даже любят это ощущение и рассматривают его как вызов — как препятствие, которое нужно преодолеть.

Что вы можете сделать, чтобы преодолеть свой страх перед математикой

1. Вам следует понять, что вы, вероятно, более сильны в математике, чем думаете сами. Когда взрослые могут применить математические методы (ведь очень многие способны распознать какие-то закономерности, выбрать лучшее из нескольких скидочных предложений в супермаркете, а также усомниться в опубликованных правительством статистических данных), они считают это проявлением «здравого смысла», а все, чего делать не могут, называют «математикой», — так что неспособность к математике становится самосбывающимся пророчеством.

2. Большинство взрослых уверены, что математика — предмет, в котором главное — усвоить ее методы и всегда все делать правильно. Мы с этим не согласны. Мы убеждены, что в математике критически важен момент, когда ты оказываешься в тупике и совершаешь ошибки. Не зря математическая задача по-английски называется «проблемой» (problem) — это потому, что для решения ее, как предполагается заранее, потребуется приложить усилия и преодолеть определенные трудности. Оказаться в тупике почетно, и зачастую лучший способ выбраться оттуда и разобраться с задачей — оставить ее на время; поговорка «утро вечера мудренее» может оказаться здесь весьма кстати.

Как научить ребёнка получать удовольствие от математики и

Ребёнок успевает по математике тем лучше, чем больше он ей занимается, и он тем скорее готов уделить ей много времени, чем сильнее она ему нравится. В значительной мере и удовольствие от занятий математикой, и их результат зависят от того, как к этому предмету относятся дома.

Один из важнейших факторов — положительная обратная связь. Вам следует хвалить ребёнка за усердие, а не за «ум» или «сообразительность». Важно помочь ему понять, что усвоение математики происходит постепенно и что очень важен постоянный рост: даже если не удается справиться с примером сразу, это не означает, что мальчик или девочка никогда не осилит его. Если же ребенок, уверовавший в свой ум или сообразительность, столкнется с математической задачей, которую пока он не в состоянии решить (что обязательно произойдет), он может подумать, будто достиг своего потолка, и сдаться.

Идеальный момент для оценки и для похвалы — во время совместной проверки домашней работы. Если ребёнок неверно решил математическую задачу, взрослому хочется сразу же сказать ему, что здесь ошибка, и объяснить, как надо правильно ответить. Не следует поддаваться такому порыву. Лучше попросить ребёнка рассказать, какие действия он выполнял, и незаметно подвести его к нужному месту так, чтобы (если вам повезет) он сам заметил ошибку.

Чтобы добиться большего, можно объяснить какую-то часть самому… и, если нужно, сделать ту же ошибку, какую сделал ребёнок, а затем исправить ее, посмеяться и сказать: «Так, дальше три плюс три, это будет семь… нет, погоди, это неверно, мама сглупила [или папа сглупил]…» Когда мальчики или девочки что-то объясняют, не торопите их; давайте детям достаточно времени, чтобы они могли описать весь ход решения.

Часто первая обнаруженная ошибка на самом деле является следствием какого-то другого, более фундаментального непонимания. Если вы позволяете довести объяснение до конца, вы, в сущности, даете ребёнку возможность самому сообразить, где он ошибся; иногда ему это удается. В итоге дети начинают понимать: ошибка — это не то, что обязательно наказуемо, и даже родители иногда ошибаются.

Когда ваш ребёнок выполнит какое-то задание по математике правильно, тоже попросите его объяснить, что и как он делал! Благодаря этому вы сможете проверить его рассуждения (иногда правильный ответ удается получить из совершенно неверных посылок), но не только; есть и другая, более важная причина. Если вы будете просить объяснения только в случаях неверного решения, ваш сын или дочь начнет связывать объяснение и ваш интерес к нему с собственной неудачей — и закроется. Вы, как родитель, ничем не сможете помочь ребенку в рассуждениях, если он не захочет описать свою логику.

Будьте терпимы к ребёнку, когда он окажется в тупике. Работая один на один с сыном или дочерью, очень легко думать: «Мне нужно донести эту мысль» или «Как это можно не понять?» Невозможно научиться чему бы то ни было мгновенно. Очень полезно сделать перерыв, вернуться к теме на следующий день или даже оставить ее на неделю. Иногда это поистине чудесно действует на понимание и усвоение темы… а также на атмосферу в доме.

Вам необходимо сделать математику увлекательным приключением, а не скучной обязанностью. И, самое главное, никогда не говорите о себе как о человеке, не способном к математике. Это самое главное наше «никогда». Если вы проявите интерес к математике, он передастся и вашим детям. А если разговоры о математике и математические игры будут естественной частью вашей повседневной жизни, а не тем, что делается только «из-под палки» за письменным столом в виде домашней работы, математика неизбежно начнет приносить удовольствие.

Фото: iStockphoto (AGrigorjeva, djedzura)

Ещё больше о детских (и не только) книгах — на «Книжной полке „Мела“» в телеграме. Там самые интересные конспекты, книжные подборки и отрывки из новинок.

mel.fm