В трех седьмых классах 70 ребят.Из них 27 занимаются в драмкружке,32 поют в хоре,22 увлекаются спортом.В драмкружке-10 ребят из хора,в хоре-6. В трех 7 классах 70 ребят из них 27 занимаются в драмкружке

Круги Эйлера. Решить задачу помогут круги Эйлера.

Задача 1.

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.

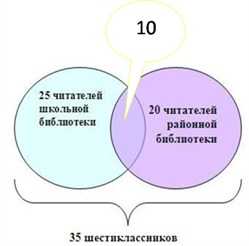
Сколько шестиклассников:

1. Являются читателями обеих библиотек;2. Не являются читателями районной библиотеки;3. Не являются читателями школьной библиотеки; 4. Являются читателями только районной библиотеки;5. Являются читателями только школьной библиотеки?

Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.

Решение.

1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)

3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)

4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)

5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).

Очевидно, что 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают.

При решении данной задачи мы использовали способ ее графического представления при помощи так называемых кругов Эйлера. Этот способ был предложен Леонардом Эйлером и широко используется при решении логических задач.

Леона́рд Э́йлер (4(15) апреля 1707, Базель, Швейцария – 7(18) сентября 1783, Санкт-Петербург, Российская империя) – швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Некоторые из его потомков до сих пор живут в России.

Рассмотрим еще один пример.

Задача 2.

Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?

Решение.

Здесь нет принципиального отличия от решения предыдущей. На готовом рисунке заменим данные: 25 на 85% и 20 на 75%. Учитывая, что все жители дома составляют 100%, заменяем 35 на 100% и получаем готовое решение: 85% + 75% – 100% = 60%.

Ответ: обе газеты выписывают 60% жителей.

Чем более сложная и запутанная логическая задача, связанная с множествами, тем более очевиден эффект от применения кругов Эйлера. Только после составления рисунка их решение становится достаточно очевидным. Задача 3.

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение.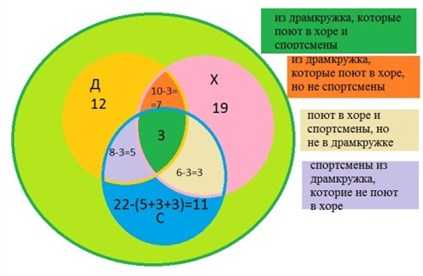

Пусть Д – драмкружок, Х – хор, С – спорт.

Тогда в круге Д – 27 ребят, в круге Х – 32 человека, в круге С – 22 ученика.

Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.

Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,

22 – (5 + 3 + 3) = 11 занимаются только спортом;

70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Ответ: 10 человек и 11 человек.

Задача 4.

В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?

Решение.

1 способ. Для решения опять воспользуемся кругами Эйлера. Пусть х человек 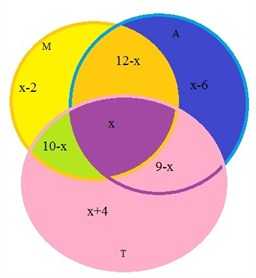пользуется всеми тремя видами транспорта. Тогда пользуютсятолько метро и троллейбусом – (10 – х) человек, только автобусом и троллейбусом – (9 – х) человек, только метро и автобусом – (12 – х) человек.

Найдем, сколько человек пользуется одним только метро: 20 – (12 – х) – (10 – х) – х = х – 2.

Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение: х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30, отсюда х = 3.

2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3. Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.

Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.

Остались вопросы? Не знаете, как решить задачу?Чтобы получить помощь репетитора – зарегистрируйтесь.Первый урок – бесплатно!

blog.tutoronline.ru

В трех седьмых классах 70 ребят.Из них 27 занимаются в драмкружке,32 поют в хоре,22 увлекаются спортом.В драмкружке-10 ребят из хора,в хоре-6

5-9 класс

спортсменов,в драмкружке-8 спортсменов;3 спортсмена посещают и драмкружок,и хор.Сколько ребят не поют в хоре,не увлекаются спортом и не занимаются в драмкружке?Сколько ребят занято только спортом?

Dinaaa 13 апр. 2016 г., 18:25:04 (2 года назад) Alferova000

13 апр. 2016 г., 20:44:06 (2 года назад)

Решать подобные задачи помогает использование диаграмм.Очертим три окружности, означающие драмкружок, спортсменов и хор. Области пересечений окружностей означают одновременную принадлежность к двум или трем категориям занятий. Начнем заполнение.1. Всем трем областям соответствует условие "3 спортсмена посещают и драмкружок, и хор)". Ставим число 3 (помечено красным).2. В драмкружке 10 ребят из хора. Следовательно, в области пересечения "Драмкружок+хор" должно находиться число 10. Но часть этой области пересекается с областью, где находятся все три категории занятий, поэтому из 10 вычитаем стоящую в этой области красную тройку и получаем число 7 (помечено синим). Т.е. посещают драмкружок и хор, но не занимаются спортом 7 человек.3. В хоре 6 спортсменов. Рассуждая аналогично (2) получаем синее число 3.4. В драмкружке 8 спортсменов. Получаем синее число 5.5. 27 ребят занимаются в драмкружке. Вычитаем из этого количества число ребят, принадлежащее общим областям 7+5+3=15 и получаем 27-15=12 человек, которые занимаются только в драмкружке.6. Аналогично получаем 11 спортсменов и 19 участников хора.7. Всего 70 учеников. Вычитая количество учеников, которые чем-либо заняты, определяем, что 10 человек не заняты ничем.8. Только спортом, как видно из рисунка, занимаются 11 человек

Ответить

informatika.neznaka.ru