Муниципальное автономное дошкольное образовательное учреждение

комбинированного вида города Тюмени

Аналитико-синтетический метод доказательства теорем в курсе геометрии 7–9-х классов. Как научить ребенка доказывать теоремы по геометрии 7 класс

Как доказывать теоремы?

Процедура доказательства теоремы только кажется сложной. Достаточно уметь логически мыслить, иметь необходимые знания по данной научной дисциплине, и доказать теорему для вас не составит труда. Важно выполнять все действия четко в правильной последовательности.

В некоторых науках, к примеру, в алгебре и геометрии, одним из важнейших умений является умение доказывать теоремы. Это связано с тем, что доказанные теоремы впоследствии пригодятся для того, чтобы решать задачи. Нужно не просто выучить алгоритм доказательства, а суметь понять ее суть. Давайте разберемся, как доказывать теоремы.

Доказательство теорем

Для начала следует сделать чертеж, он должен быть четким и аккуратным. После этого нужно отметить на нем заданные условия. В графе «Дано» нужно записать все величины, которые вам изначально известны, и то, что нужно доказать. После этого можно заняться доказательством. По сути, это цепочка логически выстроенных мыслей, которые позволяют показать то, что какое-либо утверждение является верным. Доказательство теоремы подразумевает использование других теорем, аксиом, применени

elhow.ru

Способы доказательства теорем и приемы решения геометрических задач

Аксиома есть очевидная истина, не требующая доказательства.

Теорема или предложение есть истина, требующая доказательства.

Доказательство есть совокупность рассуждений, делающих данное предложение очевидным.

Доказательство достигает своей цели, когда при помощи его обнаруживается, что данное предложение есть необходимое следствие аксиом или какого-нибудь другого предложения, уже доказанного.

Всякое доказательство основано на том начале, что при правильном умозаключении из истинного предложения нельзя вывести ложного заключения.

Состав теоремы. Всякая теорема состоит из двух частей, a) условия и b) заключения или следствия.

Условие иногда называют предположением. Оно дано и поэтому иногда получает название данного.

Обратная теорема. Предложение, у которого заключение данной теоремы делается условием, а условие заключением, называется теоремой обратной данной.

В таком случае данная теорема называется прямой.

Две теоремы в совокупности, прямая и обратная, называются взаимно-обратными теоремами.

Они находятся в таком взаимном отношении, что, выбрав любую из них за прямую, можно другую принять за обратную.

В двух взаимно-обратных предложениях одно из них вытекает как необходимое следствие другого.

Если в теореме мы обозначим условие буквой, стоящей на первом месте, а заключение буквой, стоящей на втором месте, то прямую теорему можно схематически представить выражением (Aa), а обратную выражением (aA).

Выражение (Aa) схематически представляет предложение: если имеет место A, то имеет место a.

Если для данного предложения (Aa) имеет место и теорема (aA), то обе теоремы (Aa) и (aA) называются взаимно-обратными теоремами.

Примером двух таких взаимно-обратных теорем могут послужить теоремы:

Первая теорема. В треугольнике против равных сторон лежат равные углы.

Вторая теорема. В треугольнике против равных углов лежат равные стороны.

В первой теореме данным условием будет равенство сторон треугольника, а заключением равенство противолежащих углов, а во второй наоборот.

Не всякая теорема имеет свою обратную.

Примером арифметического предложения, не имеющего своего обратного, может послужить следующая теорема. Если в двух произведениях множители равны, то и произведения равны.

Обратное предположение несправедливо. Действительно, из того, что произведения равны, не следует, что множители равны.

Примером геометрического предложения, для которого обратное предложение не имеет места, может послужить теорема: во всяком квадрате диагонали равны.

Предложение обратное этому будет: если диагонали четырехугольника равны, то он будет квадратом.

Это предположение неверно, ибо диагонали бывают равными не в одном квадрате.

Так как обратное предположение не всегда справедливо, то каждый раз обратное предложение требует особого доказательства.

В теории геометрических доказательств весьма важно иногда знать, когда данное предложение допускает свое обратное.

Для этой цели может послужить следующее правило обратимости. Когда в предположении всем возможным и различным условиям соответствуют все возможные и различные заключения, обратное предложение имеет место.

Рассмотрим для примера.

Прямое предложение. Если два треугольника имеют по две равные стороны, то третья сторона будет больше, равна или меньше третьей стороны другого треугольника, смотря по тому, будет ли угол между равными сторонами больше, равен или меньше соответствующего угла другого треугольника.

В этом предложении трем различным и возможным предположениям об угле соответствуют три различных и возможных заключения о противолежащей стороне, поэтому, согласно с правилом обратимости, данная теорема допускает обратное предположение:

Когда два треугольника имеют по две равных стороны, угол между ними будет больше, равен или меньше соответствующего угла другого треугольника, смотря по тому, будет ли третья сторона больше, равна или меньше третьей стороны данного треугольника.

Кроме обратной прямая теорема может иметь свою противоположную.

Противоположная теорема есть такая, в которой из отрицания условия вытекает отрицание заключения.

Противоположная теорема может иметь свою обратную.

Чтобы обобщить все эти теоремы, мы их представим схематически в следующей общей форме:

Прямая или основная теорема. Если имеет место условие или свойство A, то имеет место заключение или свойство B.
Обратная. Если имеет место B, то имеет место A.
Противоположная. Если не имеет места A, то не имеет места B.
Обратная противоположной. Если не имеет места B, то не имеет места A.

Следующие примеры поясняют на частных случаях взаимное отношение этих теорем:

Прямая теорема. Если при пересечении двух данных прямых третьей соответственные углы равны, то данные прямые параллельны.
Обратная теорема. Если две прямые параллельны, то при пересечении их третье, соответственные углы равны.
Противоположная. Если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
Обратная противоположной. Если прямые не параллельны, соответственные углы не равны.

При геометрическом изложении теорем достаточно доказать только две из этих трех теорем, тогда остальные две теоремы справедливы без доказательства.

На этой связи теорем основан прием, по которому для доказательства обратной теоремы ограничиваются часто только доказательством теоремы противоположной.

Способы геометрических доказательств

Для доказательства геометрических теорем существует два основных способа: синтетический и аналитический.

Эти методы называют иногда сокращенно синтезом и анализом.

Синтез есть такой метод доказательства, в котором данное предложение является необходимым следствием другого, уже доказанного.

В синтезе цепь доказательств начинается с какого-нибудь известного предложения и оканчивается данным предложением. При доказательстве исходное предложение сопоставляется с аксиомой или с другим уже известным предложением. Синтетический способ удобен для вывода таких новых предложений, которые заранее не обозначены. Для доказательства же данного предложения он представляет много неудобств. В нем не видно: a) какую из известных теорем нужно выбрать для того, чтобы доказываемое предложение вытекало как ее необходимое следствие, и b) какое из следствий выбранного предложения приводит к доказываемому предложению.

Синтез называют поэтому не методом открытия новых истин, а методом их изложения.

Впрочем и при самом изложении теорем методом синтетическим является неудобство в том отношении, что не видно, почему за исходную истину в цепи доказательств выбрано то, а не другое предложение, то, а не другое его следствие.

Примером синтетического способа доказательства может послужить следующая теорема.

Теорема. Сумма углов треугольника равна двум прямым.

Дан треугольник ABC (черт. 224).

Требуется доказать, что A + B + C = 2d.

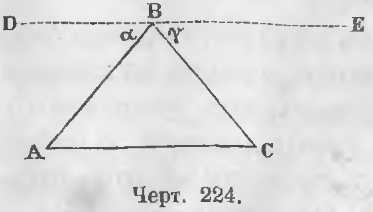
Доказательство. Проведем прямую DE параллельную AC.

Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно,

α + B + γ = 2d

Так как

α = A, γ = C

то, заменяя в предыдущем равенстве углы α и γ равными им углами, имеем:

A + B + C = 2d (ЧТД).

Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, лежащих по одну сторону прямой.

Она поставлена в связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною.

Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.

Анализ есть способ обратный синтезу. В анализе цепь рассуждений начинается доказываемой теоремой и оканчивается какой-нибудь другой уже известной истиной.

Анализ является в двух видах. От доказываемого предложения мы можем перейти к предложению, служащему его ближайшим основанием или его ближайшим следствием.

Переходя от данного предложения к предложению, служащему его ближайшим основанием, мы смотрим на данное предложение как на необходимое следствие.

Переходя от данного предложения к его ближайшему следствию, мы смотрим на данное предложение как на основание для цепи умозаключений.

Первый способ анализа. Совершая анализ переходом к основанию, отыскивают то первое ближайшее предложение, из которого данное вытекает как необходимое следствие. Если это предложение было прежде доказано, то доказано и данное предложение, если же нет, то отыскивают второе предложение, служащее основанием для первого.

Такой переход к основанию следует продолжать до тех пор, пока не дойдем до предложения вполне доказанного. Данное предложение явится как необходимое следствие последнего доказанного предложения.

Обозначая каждое предложение буквой и ставя ее впереди или позади другой, смотря по тому, будет ли оно служить основанием или следствием другого предложения, мы схематически можем этот прием анализа выразить в виде

H — K — L — M

где M есть данное предложение, L его ближайшее основание, а H предложение, вполне доказанное. Если верно предложение H, то верно предложение K; если верно K, то верно L; если верно L, то верно и M.

Второй способ анализа состоит в переходе от данного предложения к его следствию. Этот прием применяют чаще, потому что легче находить необходимое следствие, нежели отыскивать основание какой-нибудь истины. По этому способу выводят из данного предложения ту теорему, которая служит его ближайшим следствием. Если это следствие есть предложение прежде доказанное, то на нем и останавливаются; если же нет, переходят к следующему ближайшему следствию и вообще продолжают такой последовательный вывод следствий до тех пор, пока не дойдут до предложения, вполне доказанного.

Если последнее предложение не верно, то и данное не верно, ибо неверное следствие нельзя получить из верного предложения.

Если же последнее предложение верно, то для убеждения в верности данного предложения требуется, чтобы были соблюдены некоторые условия.

Схематически этот прием анализа можно представить в виде

M — N — O — P — Q — R — S

где M данное предложение, N предложение, служащее его ближайшим следствием, а S то последнее предложение, в справедливости которого мы вполне убеждены.

Из двух предложений R и S, стоящих в такой связи, что если справедливо R, то справедливо и предложение S, мы, как известно, не всегда можем обратно заключать, что если справедливо S, то справедливо и предложение R.

Чтобы последнее заключение имело место, требуется, чтобы теоремы R и S были взаимно-обратными предложениями.

Итак, для того, чтобы убедиться, что теоремы R и S стоят в такой связи, что она удовлетворяет схеме R — S и схеме S — R, требуется доказать, что предложения R и S взаимно-обратны.

Таким образом, чтобы можно было по верности последнего предложения S заключить о верности данного предложения M, требуется доказать, что каждые два рядом стоящие предложения R и S, P и R, O и P, N и O, M и N удовлетворяют закону обратимости.

Если это доказано, то цепь предложений можно обратить, и рядом со схемой M — N — O — P — Q — R — S справедлива и схема

S — R — Q — P — O — N — M

по которой мы имеем право заключить, что если справедливо предложение S, то справедливо и предложение M.

Так как затруднительно всякий раз доказывать обратимость двух предложений, то этого избегают, соединяя способ аналитический с синтетическим. После того, как из предложения M выведено предложение S как его следствие, смотрят, нельзя ли обратно вывести предложение M как необходимое следствие предложения S.

Если синтез есть способ, называемый дедукцией или выводом, то анализ можно назвать редукцией (приведение, наводка).

Примером аналитического способа доказательства может послужить следующая теорема.

Теорема. Диагонали параллелограмма пересекаются пополам.

Доказательство. Если диагонали пересекаются пополам, то треугольники AOB и DOC равны (черт. 225). Равенство же треугольников AOB и DOC вытекает из того, что AB = CD как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ как накрест-лежащие углы.

Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до предложения уже доказанного.

Сравнение синтеза с анализом. Способ аналитический вернее ведет к доказательству данной теоремы, ибо от данной теоремы легче переходить к его ближайшему основанию или следствию.

Хотя анализ лучше синтеза объясняет, почему выбран тот или другой путь для доказательства теоремы, однако неопределенность при доказательствах не устраняется вполне в том смысле, что при последовательных заменах одного предложения другим, мы не всегда можем дойти до предложения нам известного, ибо иногда не видно, какое из следствий или какое из оснований данного предложения нужно выбрать для того, чтобы его доказать. Затруднения увеличиваются еще больше, когда приходится для доказательства проводить новые вспомогательные прямые. Иногда трудно дать верные указания, какие из них облегчают доказательство данной теоремы.

Анализ, как и все логические приемы, только облегчает и помогает находить доказательство данного предложения, но не всегда необходимо ведет к самому доказательству.

Кроме этих прямых существует непрямой способ доказательства, известный под именем доказательства от противного или способа приведения к нелепости.

Способ доказательства от противного состоит в том, что для доказательства данного предложения убеждают в невозможности предположения противоположного.

На этом основании это доказательство называется доказательством от противного. Оно достигает своей цели всякий раз, когда из двух предложений, данного и противоположного, одно непременно имеет место.

В этом случае для доказательства данного, допустив противоположное предложение, выводят из него такие следствия, которые противоречат аксиомам или теоремам, уже доказанным. Если одно из следствий этого предложения ложно, то и противоположное предложение ложно, а следовательно данное предложение справедливо.

Этот прием часто применяют для доказательства теорем обратных или противоположных данным.

Не трудно заметить, что этот способ есть второй способ анализа, в котором от данного предложения последовательно переходят к его следствиям.

Примером применения такого способа может послужить приведенное выше доказательство теоремы: против равных углов в треугольнике лежат равные стороны (теорема 26).

В геометрии также применяют способы, зависящие от самого содержания геометрических истин. Геометрические истины относятся к геометрическим протяжениям. Эти протяжения обладают определенными свойствами, подлежащим внешним чувствам. Геометрическое протяжение может рассматриваться как целое, доступное наблюдению внешними чувствами. Убедительности доказательства содействует и самое чувственное созерцание. Обойтись без него в геометрии невозможно.

К числу приемов, имеющих место в геометрии, принадлежат: способ наложения, способ пропорциональности и способ пределов.

Способ наложения состоит в том, что одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений, смотря по тому, совмещаются или не совмещаются ни при наложении.

Способ пропорциональности состоит в применении к геометрическим протяжениям свойств пропорций. Этот способ применяется при доказательстве теорем, относящихся к подобным фигурам и к пропорциональным отрезкам.

Способ пределов состоит в том, что вместо данных протяжений рассматривают свойства протяжений близких по своим свойствам к данному, и выводы, получаемые из рассмотрения одних, применяют к другим сходным протяжениям.

Способы решения геометрических задач

При решении геометрических задач синтез и анализ применяют точно так же как и при доказательстве теорем.

Решая задачу синтетически, берут такую другую задачу, которую умеют решить, потом из ее решения выводят решение следующей задачи, как ее необходимое следствие, и поступают так до тех пор, пока не доходят до решения данной задачи.

Синтетический метод решения задачи обладает всеми теми же недостатками, какими обладает и синтетический метод доказательства.

Поэтому чаще и успешнее для решения задач применяют анализ.

При решении задачи анализом заменяют данную задачу новой. Эту новую задачу будем называть заменяющей.

Если две задачи находятся в таком отношении, что условия второй есть необходимые следствия условий первой, то первую задачу будем называть начальной, а вторую — производной.

При анализе существуют два способа.

Первый способ. Заменяющую задачу выбирают так, чтобы условия данной задачи вытекали как необходимое следствие условий новой заменяющей задачи, т. е. по нашей терминологии от данной задачи переходят к первой начальной задаче. Если решение этой задачи известно, то решение данной является как необходимое следствие решения начальной задачи. Если же ее решение неизвестно, то от нее переходят ко второй, третьей начальной задаче и продолжают так поступать до тех пор, пока не получат задачу, решение которой известно.

Решив эту последнюю задачу, вместе с этим последовательно доходят и до решения данной задачи.

Второй способ. Можно переходить от данной задачи к такой другой, условия которой являются следствием условий данной, т. е. от данной задачи переходят к ее производной.

Заменяя таким образом последовательно одну задачу другой ее производной, мы можем дойти до задачи, решение которой уже известно. Решение этой задачи дает иногда возможность решить и данную задачу.

Такой переход от данной задачи к ее производной применяют чаще, ибо переходить к следствию легче, нежели подыскивать основание для какой-нибудь истины.

В этом частном случае анализа обыкновенно полагают, что задача решена, и из этого предположения выводят соотношения, дающие возможность решить данную задачу.

При переходе от данной задачи к ее заменяющей весьма важно обращать внимание на то, будут ли две задачи обладать свойством взаимной обратимости. Эта взаимность в условиях двух задач является тогда, когда одна задача, будучи начальной для другой, может быть в то же время и ее производной; иначе когда две задачи находятся в таком отношении, что условия одной могут быть и необходимыми следствиями другой и наоборот.

Если две задачи, данная и новая, обладают такими свойствами, то новая задача вполне заменяет данную. В этом случае все решения одной будут и решениями другой.

Если же условия двух задач не обладают свойствами взаимной обратимости, то, заменяя данную задачу новой, мы можем найти или лишние решения или иметь некоторые из решений потерянными.

Если заменяющая задача будет производной для данной, то мы можем найти некоторые лишние решения; если же она будет начальной для данной, то мы можем найти некоторые решения потерянными.

Так как чаще от данной задачи переходят к задаче производной, то чаще приходится получать решения лишние.

Чтобы отделить лишние решения и отыскать потерянные, поверяют все найденные решения.

Поверка есть способ отделения посторонних (лишних) решений. Она дополняет анализ.

Аналитическое решение задачи указывает на то построение, которое нужно сделать для решения задачи. Совершая это построение, поступают при решении задачи способом обратным анализу, т. е. прибегают к синтетическому способу. Этот синтетический способ часто может заменить и самую поверку найденных решений.

Совместное применение синтеза и анализа дает средство избегнуть тех ошибок, которые могут получиться при применении только одного из этих методов решения.

Решим одну и ту же задачу синтетически и аналитически. Для примера может послужить следующая задача.

Задача. Разделить данный отрезок AB в крайнем и среднем отношении.

Решение. Восставим из конца отрезка AB перпендикуляр BO равный половине AB (черт. 226). Из центра O опишем окружность радиусом BO, соединим центр O с точкой A и отложим на отрезке AB отрезок AC равный AD, тогда отрезок AC или AD будет искомый.

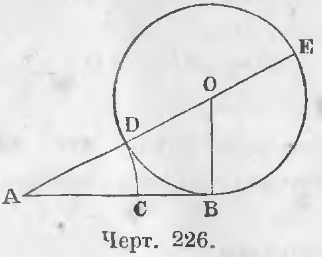
Доказательство. Прямая AB — касательная к окружности, следовательно

AE/AB = AB/AD

откуда имеем:

(AE - AB)/AB = (AB - AD)/AD

Так как DE = AB и AD = AC, то в предыдущей пропорции имеем:

AE - AB = AE - DE = AD = ACAB - AD = AB - AC = BC

откуда имеем пропорцию

AC/AB = BC/AC

Это решение синтетическое. В нем мы отправляемся от известной теоремы о свойствах касательной и решение данной задачи вытекало как необходимое следствие этой теоремы.

Решение аналитическое. Допустим, что задача решена, а следовательно и отрезок AC найден, тогда

AB/AC = AC/CB (1)

откуда

(AB + AC)/AB = (AC + CB)/AC

или

(AB + AC)/AB = AB/AC (2).

Из последней пропорции видно, что AB есть касательная, AB + AC пересекающаяся, AC ее внешний и AB внутренний отрезок.

Отсюда вытекает и само построение. Нужно из конца B восставить перпендикуляр равный ½AB, провести окружность, соединить O с A и отложить на отрезке AB часть AC = AD.

В этом аналитическом решении мы данную задачу, удовлетворяющую условию (1), заменяем задачей, удовлетворяющей условию (2).

Условие (2) указывает и путь для решения самой задачи построением.

Обыкновенно, найдя решение задачи способом аналитическим, совершают построение, в котором, применяя способ рассуждений синтетический, доказывают, что это построение действительно разрешает задачу и этим доказательством заменяют поверку, имеющую в виду устранить посторонние решения.

В данном примере между задачами, удовлетворяющим условиям (1) и (2), существует полная обратимость, ибо из условий (1) вытекают условия (2) как необходимое следствие и наоборот, поэтому здесь нет ни потерянных, ни посторонних решений.

Исследование второстепенных и вспомогательных приемов решения задач еще не достигло в своей обработке полной и совершенной законченности. Мы пока устраняемся от их подробного рассмотрения.

maths-public.ru

Аналитико-синтетический метод доказательства теорем в курсе геометрии 7–9-х классов

Разделы: Математика, Общепедагогические технологии

«Аналитико-синтетический метод доказательства теорем в курсе геометрии 7-9-х классов»

Эффективность процесса обучения математике в наше время определяется многими факторами. От мастерства учителя, его умения управлять процессом формирования знаний учащихся, развитием их способности мыслить во многом зависит, сможет ли ученик творчески подойти к изучаемому материалу. Его задача, прежде всего, воспитать активно мыслящую личность.

Приобретая математические знания умения, учащиеся должны научиться проводить аргументированные доказательства, овладеть такими сложными категориями как определение, классификация, анализ и синтез, получить навыки индуктивных и дедуктивных рассуждений.

Часто приходиться сталкиваться с такими случаями, когда учащийся заучивает учебный материал, без осмысления, набивает себе руку в пользовании определенными алгоритмами и обладает ленью разума, которая мешает ему продумать встретившиеся трудности.

Сильно мешает изучению математики отсутствие привычки внимательно следить за цепочкой логических выводов, критически их осмысливать, замечать отсутствие необходимых для полноты вывода звеньев рассуждений.

Иногда учащиеся не только плохо справляются с отыскиванием этих звеньев, но и не видят надобности в самом логическом доказательстве.

В предложенной работе была сделана попытка выработки единой методики обучения учащихся умению построить логически безошибочные схемы доказательств, а также привитие им навыков к скрупулезной работе в поисках обоснования любого более или менее важного шага в ходе доказательства.

Обучение учащихся доказательству теориям нередко оказывается недостаточно эффективным. На уроках математики видно, что многие ребята затрудняются в решении задач на доказательство, допускают ошибки при обосновании решения задачи. Одна из причин этого – недостаточное освещение в школьных учебниках различных способов доказательства, что приводит к заучиванию и формальному усвоению учебного материала без критического осмысления. Среди других причин обращает на себя внимание тот факт, что доказательства данные в учебнике, проведены только синтетическим путем. Преимущества этого способа общеизвестны.

Учащиеся получают образцы последовательности, четкости и лаконизма изложения. Но вместе с тем при этом скрыт ход рассуждений, который привел к доказательству. Синтез, оторванный от анализа, при формальной безупречности выводов приводит порой, как это ни парадоксально к алогизму.

В теории обучения проблему аналитического и синтетического метода зачастую рассматривают без учета фактора времени: сегодня «учат» первому на одной задаче или теореме, завтра второму на совершенно другой задаче. Анализ не будет пустым, а синтез будет содержательным, если мы эти два метода будем рассматривать, как единый процесс доказательства.

Обучение решению задачи или доказательству теоремы с помощью двуединого анализа–синтеза обретает особую значимость на уроках геометрии.

Рассмотрим пример.

Пусть требуется доказать теорему о признаке параллелограмма.

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм.

В методических руководствах приводят одно изолированное так называемое синтетическое доказательство.

Вот оно:

Рассмотрим треугольник АОД и СОВ: ВО=ОД, АО=ОС по условию, <ВОС=<ДОА, как вертикальные, следовательно <АОД=<СОВ по первому признаку. Значит, углы равны, а они являются внутренними накрест лежащими при прямых ВС и АД и секущей АС. По признаку параллельности прямые ВС и АД параллельны. Параллельность прямых АВ и СД доказывается с помощью равенства треугольников ВОС и ДОС. Теорема доказана.

Крайняя трудность запоминания таких доказательств объясняется психологической произвольностью первого шага для ученика: в самом деле, почему «вздумалось» учителю начинать доказательство именно с треугольников АОД и СОВ? Откуда он их взял? Как запомнить ученику этот исходный пункт доказательства? Вот в чем вопрос.

Подобная методологическая линия приводила (и все еще приводит) – как это верно описано Д.И. Писаревым – к тому что «математика представляется ученику рядом удивительных фокусов, каждый из которых имеет свой особенный ключ, и это сотню ключей школьник вынужден осилить памятью, а не логикой».

Немаловажную роль в обучении доказательству теорем играет запись этого доказательства. Традиционно записать доказательства представляет собой что-то вроде конспекта, самого доказательства, в котором отмечены основные моменты для заполнения. Такая запись сможет оказать определенную помощь ученикам в заучивании, но не направляет их мысли. Очень часто мы встречаемся на уроках с такими фактами, когда ученик у доски добросовестно пересказывает зафиксированные в тетрадях шаги доказательства, а почему именно выбран тот или иной шаг он объяснить не может. Поэтому возникает необходимость в системе четкой записи доказательств теорем, т.е. нам нужна такая запись, которая бы подробно со всеми логическими обоснованиями и в то же время кратко в описании представляло нам запись доказательства теоремы.

Наиболее эффективным будет обучение доказательства теорем аналитико-синтетическим методом, т.е. надо идти к синтезу через анализ, трактуя их как двуединый процесс, как продолжение одного другим. Приведем соответствующее доказательство к выше отмеченной теореме.

Требуется доказать, что ВС параллельно АД.
Для этого достаточно доказать, чтобы внутренние накрест лежащие углы ВСО и ОАД, образованные прямыми ВС и АД и секущей АС были равны.
А для того, чтобы доказать, что эти углы равны надо доказать равенство треугольников ВОС и ДОА, и что интересующие нас углы лежат против соответственно равных сторон. В последнем убеждаешься из чертежа, так как ВО=ОД по условию.
Для того, чтобы треугольники ВОС и ДОА были равны достаточно доказать либо первый, либо второй, либо третий признак равенства треугольников. В данном случае нам удобнее доказать первый признак, т.к. ВО=ОД и СО=ОА по условию теоремы, а углы ВОС и ДОА равны, как вертикальные.

Далее составляем схему проведенного анализа:

Чтобы доказать --------->	Надо доказать
I. ВС \|\| АД	II.<ВСО=<ОАД, как внутренние накрест лежащие, образованные прямыми ВС, АД и секущей АС
II. <ВСО=<ОАД	III. ?ВОС=?ДОА, и углы ВСО и ОАД лежат против равных сторон
III. Треугольник ВОС= Треугольник ДОА	IV. Равенство трех его элементов и определить признак равенства треугольников ОА=ОС – по условию ВО=ОД – по условию <АОД=<СОВ – вертикальные Треугольник ВОС= Треугольник ДОА по I. признаку
ТО <--------------	ЕСЛИ

Идя слева направо мы осуществляем анализ доказательства (I>II>III>IV), перебираясь каждый раз от заключения к его основанию, рассуждая по схеме: «чтобы доказать (I), надо доказать (II) и т.д.»

Иначе говоря, мы создаем здесь цепь необходимых условий: каждое верхнее суждение есть необходимое условие для нижнего. Теперь остается главное – соединить оба процесса, анализ завершить синтезом. Пусть ученик проведет рассуждение справа налево (IV>III>II>I), нанизывая цепь достаточных условий от основания к заключению, и рассуждая так: «если IV, то III, если III, то II и т.д.»

Двустороннее движение мысли, обучение анализу, немедленно перерастающему в синтез – вот одно из направлений совершенствование дидактики.

Анализ ведет к более глубокому и сознательному усвоению учебного материала и способствует активному и творческому развитию логического мышления учащихся, нежели синтез, но как уже отмечалось, анализ будет полезен только тогда, когда он ведет к созидательной работе, т.е. анализ и синтез неотделимы друг от друга. Предлагаемая методика является хорошим инструментом для воспитания у учащихся потребностей обосновывать каждый шаг. Хотя первоначальное знакомство с таким обучением и требует значительной затраты времени, но в дальнейшем это все окупается. Чтобы такой урок дал эффект учителю необходимо продумывать каждый шаг, вести школьников от ступеньки к ступеньке, следить, чтобы мысли учащихся шли в нужном направлении, чтобы не ускользало от их внимания главное, чтобы все даже самые слабые ученики принимали участие в открытии нового. Не всегда, конечно, можно его применить, но там где это, возможно, наблюдается наиболее глубокий интерес школьников, развивается логическое мышление, повышается познавательная активность.

Такая кропотливая работа, в конечном счете, приносит свои плоды, ибо ученики приобретают исследовательские навыки и, что не менее важно, с большим интересом работают на уроке.

xn--i1abbnckbmcl9fb.xn--p1ai

Доказательства по геометрии 7 класс. | Геометрия

Добрый день, дорогие друзья! Сегодня мы с вами поговорим про задачи на доказательства по геометрии 7 класса. В геометрии, в отличии от алгебры, есть очень много задач на доказательство тех или иных тем. В таких задачах, как правило, очень мало вычислительного материала, зато очень много логических рассуждений, связанных между собой цепочкой доказательств. Здесь важно выделить конец доказательства, а затем, идя к началу, раскручивать его. Как это происходит, мы сегодня разберём.

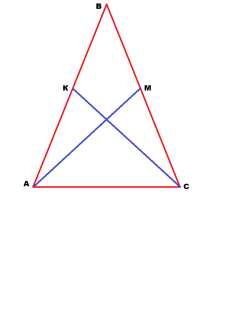Задача 1. Докажите, что медианы, проведённые к боковым сторонам равнобедренного треугольника, равны. Доказательство. Предположим, что мы доказали равенство медиан.Смотрим, в каких фигурах эти медианы находятся, и что можно сказать об этих фигурах.Итак, медианы АМ и СК находятся в треугольниках АМС и АКС или в треугольниках АВМ и СВК. Для доказательства равенства медиан надо доказать равенство треугольников.Выбираем первую пару. Треугольники АМС и СКА. Поскольку треугольник АВС равнобедренный, то АВ=ВС.Но медиана делит противоположную сторону треугольника пополам. Отсюда АК=КВ=СМ=ВМ. Или АК=СМ.Углы при основании равнобедренного треугольника равны. Получается ∠А=∠С. Теперь вернёмся опять к треугольникам АМС и СКА. У них АК=СМ.Угол МСА равен углу КАС, а сторона АС — общая.Получается, треугольники равны по первому признаку равенства треугольников.А в равных треугольниках против равных углов лежат равные стороны.Против угла МСА в треугольнике АМС лежит сторона АМ, а против угла КАС в треугольнике СКА лежит сторона КС. Значит, эти стороны равны.Медианы, проведённые к боковым сторонам равнобедренного треугольника, равны.

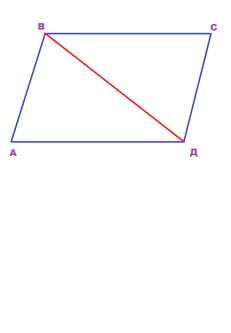Задача 2. Докажите, что диагональ параллелограмма разбивает его на 2 равных треугольника. Доказательство. И опять, как в задаче 1. Предположим, что треугольники АВД и ВСД равны.Диагональ параллелограмма принадлежит обоим треугольникам. Т.е. у них одна сторона общая.Осталось найти либо 2 пары равных углов, либо равные стороны и два равных угла, либо по две равных стороны.У параллелограмма, как мы знаем, противоположные стороны равны.Имеем АД=ВС, АВ=СД. Получается, что треугольники равны по трем сторонам. Можно доказать по другому, согласно 2 признаку равенства треугольников. В треугольниках АВД и ВСД углыСВД и ВДА равны, как накрест лежащиепри параллельных прямых ВС и АД и секущей ВД.Углы ВДС и АВД равны, как накрест лежащие при параллельных прямых АВ и СД и секущей ВД.Получается, что треугольники равны по стороне и двум прилежащим к ней углам.

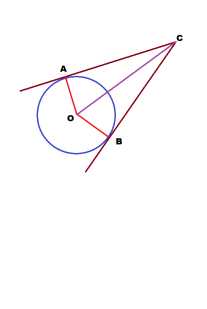Задача 3. Докажите, что отрезки касательных, проведённых к окружности из одной точки, равны.Доказательство. Нам дано, что из точки С проведены 2 касательных АС и ВС к окружности.Для того, чтобы провести доказательство равенства сторон, сделаем дополнительные построения.Проведём радиусы ОА и ОВ, а также прямую ОС. Доказав равенство треугольников ОАС и ОВС, мы сможем доказать равенство сторон АС и ВС.Мы знаем, что радиусы, проведённые в точку касания перпендикулярны касательной. Поэтому, углы ОАС и ОВС — прямые.Отсюда, треугольники САО и СВО — прямоугольные.Эти треугольники равны, т.к. катеты ОА и ОВ равны, а гипотенуза ОС у них общая. Прямоугольные треугольники равны по катету и гипотенузе.А в равных треугольниках против равных сторон лежат равные углы. Против стороны ОА лежит угол АСО, а против стороны ОВ — угол ВСО.Эти углы равны. А если 2 угла одного треугольника соответственно равны двум углам другого треугольника, то и третьи углы у них равны.Значит, углы ВОС и АОС равны.А в равных треугольниках против равных углов лежат равные стороны.Против угла АОС лежит сторона АС, а против угла ВОС — сторона ВС.Углы равны, значит и стороны АС и ВС равны.

На сегодня, пожалуй, достаточно. Ведь скоро Новый Год, все мысли о нём,так что геометрию ненадолго отложим в сторону.Спасибо всем и с НОВЫМ ГОДОМ!

Вам так же будет интересно:

Оставить комментарий

geometriyaprosto.ru

Методические подходы изучения первых теорем геометрии в 7 классе. Введение

ОГЛАВЛЕНИЕ.

МЕТОДИЧЕСКИЕ ПОДХОДЫ ИЗУЧЕНИЯ ПЕРВЫХ ТЕОРЕМ ГЕОМЕТРИИ В 7 КЛАССЕ.

Введение .........................................................................................................................................1-4
Особенности обучения доказательству теорем в курсе геометрии 7 класса………………....4-7
Методические подходы к изучению теорем по учебнику Л.С.Атанасяна…………………...7-8

§ 3. Результаты педагогического эксперимента……………………………………………………....8-25

Заключение ………………………………………………………………………………….…………26-27

Использованная литература …………………………………………………………………………..28-30

„Методические подходы изучения первых теорем геометрии в 7 классе“

ВВЕДЕНИЕ.

Современный этап развития образования способствует проведению реформирования и модернизации системы образования. На каждом этапе развития перед обществом возникают новые задачи, которые требуют переосмысления имеющихся у человечества теоретических знаний и практических умений. Приоритетным направлением в современном образовательном процессе называют гуманизацию и гуманитаризацию. Новые целевые установки в системе образования предполагают направленность обучения на развитие личности, в частности на формирование логического мышления, чему способствует обучение доказательству. Формирование и использование умений рассуждать, проводить доказательства, аргументировать высказывания проводится во всех учебных предметах. Однако бесспорно, что развитию способностей школьников анализировать данные, принимать решения и обосновывать свой выбор в наибольшей мере способствует изучение математики. Основную нагрузку по формированию у учащихся умения доказывать несёт курс геометрии. Методы рассуждения и доказательства, обоснование собственного мнения и психическая деятельность, связанная с поиском доказательства, сходны и в жизненных, и в производственных, и в школьных задачах. Поэтому ознакомление учащихся с методами и приёмами рассуждения и доказательства является средством улучшения учебных навыков учащихся, их воспитания и подготовки к будущей производственной деятельности. Обучение учащихся проведению доказательства - проблема сложная и многоаспектная. Она занимала и занимает в психолого-педагогической науке и в теории обучения математики одно из ведущих мест. Вопросам понимания сущности доказательства, поиска доказательства, обучения проведению доказательства посвящено огромное количество исследований. В настоящее время модернизация образования предусматривает выбор детьми профиля обучения в старшем звене. Для создания условий выбора учащимися в 10 классе математического профиля для дальнейшего обучения, для развития положительной мотивации изучения геометрии и формирования прочных навыков доказательства, на котором построен школьный курс геометрии 10-11 класса, работу по обучению школьников доказательству надо начать вести в 7 классе.

Проблема обучения учащихся доказательству всегда являлась одной из центральных в методике преподавания математики.

^ что в настоящее время работа с учащимися «носит однобокий характер» и акцент делается только на умение решать задачи, а формирование культуры математической речи, культуры доказательств отступает на второй план. Особенно плохо обстоит дело с обучением доказательству. Прежде всего, это связано с внедрением тестовых проверок знаний и умений учащихся. Таким образом, обнаруживается противоречие. С одной стороны, доказательства являются источником и условием развития логического, абстрактного, дедуктивного и эвристического мышления учащегося, являются способом систематизации учебного материала, средством мотивации и получения обучаемым новых знаний, в процессе доказательств развиваются важнейшие интеллектуальные и учебные умения. А с другой стороны, именно в этом направлении не ведется достаточно систематической работы.

Все вышесказанное определяет актуальность проблемы исследования, состоящей в разрешении указанного противоречия посредством разработки методических подходов в обучении доказательству учащихся, начиная с 7 класса.

^ процесс обучения геометрии в 7 классе общеобразовательной школы.

Предметом исследования является обучение доказательству теорем в курсе геометрии 7 класса.

^ в разработке методических подходов обучению доказательству в курсе геометрии 7 класса общеобразовательной школы.

Для достижения цели исследовательской работы поставлены следующие задачи:

Изучить и проанализировать педагогическую, научно – методическую, учебную, учебно-методическую литературу по теме исследования;
Проанализировать теоретические основы обучения доказательства в курсе 7 класса;
Составить методическую разработку обучения доказательствам в курсе 7 класса общеобразовательной школы.
Экспериментально проверить методику применения составленной разработки, при изучении геометрии 7 класса.

Гипотеза: привитие учащимся правильного представление о нахождении оптимального подхода к доказательству теорем, а также стремления к самостоятельному поиску и проведению доказательств будет более эффективным, если обучение их доказательству будет основано на следующих положениях:

необходимость чёткой формулировки посылок и заключения математических утверждений, без выявления которых невозможен процесс доказательства;
выделение каждого шага доказательства и их мотивирование, явное выявление общей стратегии проведения доказательств;
аргументация каждого шага проведённого доказательства в виде ссылок на соответствующие определения, аксиомы, теоремы, ранее решенные задачи;
чертежи, используемые при доказательстве, должны приводиться в соответствии с выполняемыми шагами доказательства; не следует все построения выполнять на одном чертеже, это может способствовать формированию у учащихся овладению необходимыми умениями для проведения доказательств в курсе геометрии 7 класса.

Методы исследования:

Анализ психолого-педагогических, методических трудов по теме исследования, изучение программ;
Наблюдение за учебно-воспитательным процессом;
Беседы, анкетирование, тестирование;
Экспериментальное обучение и обработка исследуемых результатов на основе математических методов исследования.

Особенности обучения доказательству теорем в курсе геометрии 7 класса.

Принципы подхода к обучению учащихся теоремам и их доказательствам следуют из двух соображений. Во- первых, теорема – это новый материал, подлежащий изучению, и с этой точки зрения в изучении ьеоремы можно выделить следующие этапы: подготовка к изучению нового, мотивация изучения нового материала, введение нового – органзация его восприятия, понимания, закрепление, применение. Во – вторых, теорема является задачей на доказательство, выражающей некоторое важное отношение, свойство, и поэтому на методику изучения теорем распространяюся рекомендации, относящиеся к различным этапам решения задач, таким как обучение анализу условия и исследоанию полученного решения.

При обучении учащихся теоремам могут иметь различные методы: объяснительно-иллюстративный, эвристический, исследовательский. Выбор метода обучения диктуется содержанием теоремы, методом её доказательства, конкретными возможностями учащихся.

Выбор метода осуществляется при логико-математическом анализе материала, подлежащего изучению.

Очень часто приходится встречаться с таким фактом, когда учащиеся заучивают формулировки теорем, не осозновая полностью их смысла. Если ученик сам находит закономерность, сам формулирует теорему, то это позволяет избавиться от фармализма в знании формулировок. Для самостоятельного получения формулировок теорем учащиеся могут использоать различные построения, измерения, модели.

Аналогично с помощью выполнения измерений, вычислений, использования наглядных пособий можно привести учащихся к самостоятельному формулированию любой теоремы. После того как закномерность учащимися выявлена, необходимо скорректировать формулировку, привлекая к этому учеников и аргументируя эту корректировку. Можно также предложить учащимся проанализировать формулировку теоремы, содержащую ошибку. Ошибки в формулировках теорем выявляются с помощью приведения контрпримеров. Эту работу можно отнети к этапу закрепления формулировки теоремы.

Для понимания формулировки и доказательства теоремы, для снятия трудносте в его использовании необходимо выделять в формулировке условие и заключение, данные и требование. Это выполнит труднее, если теорема сформулирована в категоричной, а не условной форме. Поэтому категоричную форму полезно переделывать в условную и наоборот, что не всегда легко осуществляется.

Переходим к вопросу краткой записи формулировки теоремы. Переход от правильной формулировки к павильной схематической записи условия и заключения является работой, требующей достатчно развитого логического мышления. В начале систематического курса геометрии возникает вопрос, на сколько подробно следует записывать условие и заключение теорем. Могут иметь место следующие рекомендации. Если схематическая запись условия теоремы вызывает существенные затруднения, то от нее в некоторых случаях вообще следует отказаться. Записи условия и заключения теоремы должно быть настолько подробными, чтобы по записи можно было полностью восстановить текст формулировки теоремы. И в то же время запись условия недолжно содержать ничего лишнего.

Доказательство теорем учащиеся могут получить с большей долей самостоятельности, если это доказательство предъявлено ученикам в виде последовательности задач. Доступно для самостоятельного решения. По поводу оформления дказательств можно высказать ряд соображений. Оформление доказательств с выделением утверждений и их обоснованием, фактов и аргументов необходимо для понимания доказательства, для понимания построения всего дедуктивного курса геометрии, для воспитания потребностей в доказательстве. Краткой записи полученных доказательств учащихся необходимо обучать специально. Следует также обучать записи доказательств представленных в учебнике. Это специльная, трудная и необходимая работа. В алгебраических доказательствах, при различных алгебраических преобразованиях используется запись аргументов под знаками равенства.

После получения и осуществления идеи доказательства теоремы, после записи доказательства теоремы необходим этап заключения полученного доказательства. Этот этап являтся закреплением самого доказательства и предшествует закреплению и применению формулировки теоремы. На уроках этот этап иногда неоправданно не находи своего места.

Этап закрепления доказательства в изучении теоремы предлагает работу по выявлению, поняты ли идея, метод доказательства и отдельные его шаги. Вопросы: „Понятно ли доказательство?“ , „Кто не понял доказательство?“ дают мало или вообще не дают информации учителю, насколько доказательство теоремы оказалось усвоенным учащимися. При осуществлении этапа закрепления полученного доказательства можно с помощью вопросов, обращенных к учащимся, снова „пройтись“ по всему доказательству, можно попросить объянить отдельные шаги доказательства, перечислить все аксиомы, теоремы и определения, которые используются в доказательстве, выяснить, где используется какие-либо данное, все ли условия оказались использованными, какое и почему дополнительное построение оказалось полезным при поиске доказательства, в чем заключается основная идея доказательства, что оказалось несущественным для доказательтва и что может быть изменено, нет ли других способов доказательства рассматриваемой теоремы, всегда ли полученное доказательтво имеет смысл. Повторение доказательства приобретает большую ценность, если оно варьирует обозначения на неизменном чертеже, а также сам чертеж. На этапе закрепления теоремы возможна работа над формулировкой теоремы, над её запоминанием, обучением узнаванию изученной теоремы в различных ситуациях и применением в простейших случаях и в различных комбинациях.

Поэлементной отработке каждого слова формулировки и её запоминанию способствует компактный метод Я.И.Груденева, когда формулировка теоремы, как и ранее рассмотренные формулировки определений, разбиваются на составные части и произносятся вслух и используются по частям. Такая работа способствует и осознанию, и запоминанию теорем.

Ещё один этап, рассматриваемый как этап изучения теоремы, - этап систематизации знаний. Известно, что никакой факт нельзя считать усвоенным, пока он не занял определенного места в имеющейся системе знаний. Понимая взаимосвязи между теоремами, ученик может восстановить самостоятельно забытые формулировки теорем, формулы. Для систематизации теорем важно выяснить место теоремы и в системе других сведений: признаком или свойством некоторого понятия является теорема, следствием каких теорем она является что является ее следствиями.

Наличие всех рассмотренных этапов при обучении каждой теореме требует большого расхода времени. И в полном, развернутом виде все этапы могут быть представлены лишь в отдельных, удобных для этого случаях. А в различных конкретных ситуациях на первый план выдвигается то один, то другой этап, предпочтение отдается то поиску формулировки, то обучению записи полученного доказательства, то поиску идеи доказательства, то исследованию – в зависимости от требований ситуации.

Трудности и ошибки учащихся при применениии теорем те же, что и при решении задач. Очень распространенной ошибкой явлется смешивание определений и теорем, признаков и свойств понятий; использование вместо прямой теорем обратной и наоборот; использование в доказательстве теоремы, которую предстоит доказать; доказательство того, что дао в теореме; использование не доказанных утверждений и другое. Все эти ошибки одного порядка – непонимание логики построения курса, логических взаимосвязей между элементами теории. В этих условиях особое значение приобретают выполнение заданий на систиематизацию понятий и теорем, выяснение логики построения формулировки и доказателсьтва теорем. При исправлении логческих ошибок учащихся необходимо учесть следующую рекомендацию: замене неверных ответов на верные должны предшествовать совместный анализ учителем и учащимися неверных ответов и выявление допущенных ошибок. Обучение доказательству, выявление допущенных при докаазтельстве ошибок – составная часть важнейшей задачи развития логического мышления.

Какие цели развития учащихся могут сравниться и решаться учителем при обучении учащихся доказывать ту или другую теорему? Это и развитие творческого мышления, и развитие логического мышления. При доказательстве теорем учащиеся учаться понимать, в чем заключается смысл доказательства; формулировать предложения в различных формах; провоит доказательство вообще: выделять тезис-требование и условия, в которых оно доказывается, разделять доказательсва на шаги и обосновывать каждый шаг; учатся неосознанному использованию законов логики и правил вывода; учатся различать прямую и обратную теорему, свойства и признаки понятий, необходимые и достаточные условия; учатся различным методам доказательства (синтетическому, аналитическому, методу от противного). А доказывать, обосновывать свою точку зрения необходимо уметь каждому культурному человеку не только в математике, но и в жизни вообще.

Выделим возможные уровни усвоения учащимися теорем. Учащийся: 1) павильно формулирует теорему, понимает каждое слово в формулировке; 2) может привести свой пример на применение формулировки; 3) может повторить доказательство; 4) понимает идею и план доказательства, может варьировать обозначения, чертеж, метод доказательства; 5) узнает и применяет теорему в знакомой ситуации; 6) знает и применяет теорему в незнакомой ситуации.

Приведенные уровни усвоения теоремы являются перечислением дидактических целей – целей обучения, которые учитель ставит на отдельных уроках по изучению той или ной теоремы. В соответствии выделенными целями строится урок – выбираются методы и формы работы, строятся системы упражнений.

Все рассмотренные этапы изучения теоремы имеют место при любом методе изучения, как при частично-поисковом, так и при объяснительно-иллюстративном. Разница – в уровне активности и самостоятельности учащихся при получении доказательства теоремы.

Результаты анализа работ В.А.Гусева, Г.И.Саранцева, Д.Пойа позволили нам разработать методические подходы к обучению доказательствам в курсе геометрии 7 класса общеобразовательной школы, основанные на следующих положениях:

Необходимость чёткой формулировки посылок и заключения математических утверждений, без выявления которых невозможен процесс доказательства;
Выделение каждого шага доказательства и их мотивирование, явное выявление общей стратегии проведения доказательств;
Аргументация каждого шага проведённого доказательства в виде ссылок на соответствующие определения, аксиомы, теоремы, ранее решенные задачи;
Чертежи, используемые при доказательстве, должны приводиться в соответствии с выполняемыми шагами доказательства; не следует все построения выполнять на одном чертеже, это может способствовать формированию у учащихся овладению необходимыми умениями для проведения доказательств в курсе геометрии 7 класса.

В методической литературе для учителей математики, учебниках методики преподавания математики для педвузов выделяют следующие способы рассуждений при доказательстве (или поиске доказательства) теорем: синтез, восходящий анализ, нисходящий анализ. Традиционно отмечают основной недостаток синтетического метода, состоящий в том, что учащиеся остаются пассивными, «слепо» следующими за рассуждениями учителя. В этом же плане выделяют преимущество аналитических приемов рассуждений.

Но, как известно, обучение аналитическим приемам рассуждений должно опираться на определенный опыт проведения синтетических рассуждений. В этой связи начинать обучать строить доказательства на основе проведения аналитических рассуждений нельзя. Это подтверждает практика обучения в школе. Опыт показывает, что большинство учащихся 7-8 классов не воспринимают рассуждения, проводимые по схеме восходящего анализа. Еще сложнее обстоит дело при использовании нисходящего анализа. Таким образом, налицо противоречие – аналитические приемы применять еще рано, а использование синтеза при доказательстве теорем и решении задач, да еще в первый год изучения систематического курса геометрии, мало способствует формированию умения доказывать самостоятельно.

Действительно, буквальное следование учителя текстам доказательств, которые мы видим в учебниках геометрии, ничего хорошего не даст. И здесь проблема не только в том, что, даже понимая доказательство, ученик не видит, как надо действовать, чтобы самому доказать тот или иной факт. То есть не решается самая главная задача обучения геометрии – научить ученика доказывать самостоятельно, раскрыв перед ним, так сказать внутреннюю «кухню» проведения доказательств.

Доказательство теорем курса геометрии представляет достаточно длинную цепь последовательно связанных дедуктивных умозаключений (логических шагов), устанавливающую истинность теоремы. Установление связи между отдельными шагами, их выделение, обоснование представляет для многих учащихся 7 класса значительную трудность. К тому же доказательства в школьном курсе геометрии содержательны, свернуты и содержат в значительной мере интуитивный компонент, а порой даже делается ссылка на утверждение отсутствующее в учебнике. Снижению этой трудности может способствовать использование специальных подходов.

Рассмотрим для примера несколько теорем курса геометрии 7-го класса и возможный вариант организации работы учащихся по их доказательствам.

^ Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Работу с теоремой можно представить поэтапно, где на первом этапе ведется работа над содержанием теоремы с применением иллюстративно – объяснительного метода.

I этап Таблица № 1

№	^	Деятельность учащихся (ответы)
1.	Устно вслух читаем теорему и делаем разбор теоремы	По выбору учителя один ученик читает теорему остальные следят.
2.	Учитель задает наводящие вопросы: 1. В чем заключается основная мысль теоремы? 2. О скольких треугольниках рассказывается в теореме? 3. Какие элементы треугольника должны быть равными?	О равенстве треугольников О двух Две стороны и угол между ними
3.	Теперь рассмотрим нашу теорему наглядно Карточка №1 (приложение 1)	(учащиеся получают карточки)
4.	Теперь рассмотрим рисунки и определим: 1.Что означает рис №1 2. Что означает рис №2 3. Что означает рис № 3 4. Что означает рис № 4 5. Как Вы думаете? Почему на рис. № 1 и № 3 стороны треугольника выделены, синим и зеленым цветом? 6. А почему на рис № 2 и № 4 угол отмечен красным цветом?	Две стороны первого треугольника Угол между сторонами первого треугольника Две стороны второго треугольника Угол между сторонами второго треугольника Равенство соответствующих сторон (синий синему, зеленый зеленому) Потому что они равны.

На втором этапе идет процесс усвоения содержания теоремы при помощи наводящих вопросов учителя и ответов на эти вопросов учащихся, выявляются факты, отраженные в теореме.

II этап Таблица № 2

№	^	Деятельность учащихся (ответы)
1	Теперь из нашей теоремы определим условие и заключение.	Условие: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника. Заключение: то треугольники равны.
2	Так как мы имеем теорему, то наша теорема должна иметь………….?	доказательство
3	Что мы должны доказать? И из чего мы должны исходить?	Исходя из заключения теоремы должны доказать равенство треугольников
4	А как Вы думаете что для этого нам достаточно знать?	По условию теоремы нам достаточно знать равенство двух соответствующих сторон у первого и второго треугольника и равенство углов между этими сторонами.

На третьем этапе проводится доказательство с выполнением отдельных друг от друга чертежей, используемых при доказательстве, приводящихся в соответствии с выполняемыми шагами доказательства, которые преподносят учащимся определенную информацию логической цепочки доказательства. Доказательство целесообразно проводить устно совместно с учащимися, проводя рассуждения постепенно. В конце доказательства учащимся выдаются фигурки треугольников, с помощью которых в процессе наложения друг на друга устанавливается истинность теоремы и тем самым наглядно демонстрируется метод наложения.

III этап

1. Рассмотрим два треугольника АВС и MNO у которых АВ=MN

Рис. 1

2. ВС=NO

Рис.2

Рис.3

4. Докажем, что АВС = MNO5. Для этого мы воспользуемся методом наложения. Смысл метода наложения заключается в том, что если АВС можно наложить на MNO и при этом треугольники полностью совместятся, то эти треугольники называются равными. Для более наглядного представления рассмотрим макеты треугольников АВС, MNO. (Учащимся раздается заранее подготовленные макеты равных треугольников).

1. Так как , наложение начнем с этих углов. При этом мы знаем из условия доказательства, что АВ=MN и ВС=NO, тогда мы обнаружили, что углы полностью совместились.

По нашему условию сторона АВ=MN, тогда вершина А совмещается с вершиной М, а вершина В совмещается с вершиной N
тогда стороны АВ и ВС наложатся соответственно на стороны МN и NO, тогда при наложении они тоже совмещаются.
Далее по нашему условию сторона ВС=NO, при этом нам известно из шага 2 доказательства, вершина В совмещается с вершиной N, и вершина С совмещается с вершиной О.
Тогда вершины А,В,С совместились с вершинами М, N,О и сторона АС совмещается со стороной МО и треугольники полностью совместились, значит они равны. Теорема доказана.

Заключительным этапом в работе с теоремой является этап закрепления доказательства в виде практического задания, где в изучении доказательства предлагается работа по выявлению, поняты ли идея, метод доказательства и отдельные его шаги.

IV этап.

Учащимся раздаются заранее подготовленные макеты треугольников АВС, OPR, MNO, KLF, SQR, MNK (работа парная).

Задание: 1) Найдите равные треугольники.

2) Как вы думаете, почему треугольники OPR и SQR не равны?

3) Как вы думаете почему треугольники MNК и KLF не равны?

4) Как вы думаете, почему треугольники OPR и АВС не равны?

Ранее приводимые записи доказательств теорем в других методиках обучения доказательств показывают, что они имеют достаточно сложную, многошаговую структуру, разобраться в которой ученикам 7 класса, только приступившим к изучению систематического курса геометрии, очень сложно. Поэтому выделить утверждения, найти им обоснования, выстроить последовательность шагов – задача для многих учеников чрезвычайно сложная. К тому же опыт показывает, что спешить с привлечением школьников к самостоятельному доказательству не следует, ученики должны сначала разобраться в структуре готовых доказательств, научиться работать с ними. На основании вышеизложенного можно выделить четыре этапа при работе с доказательством теоремы курсе 7 класса общеобразовательной школы:

Работа над содержанием теоремы. На этом этапе учитель специальными вопросами помогает пониманию значения каждого слова в формулировке теоремы, способствует зрительному восприятию содержания теоремы с помощью специальных карточек, моделирующих условие теоремы.
Усвоение содержания теоремы. На этом этапе выявляется условие и заключение теоремы, выявляются факты, отраженные в теореме.
Этап проведения доказательства. Изучение доказательства с помощью специально подобранных чертежей и сопутствующих упражнений, в процессе которых постигаются детали доказательства, цепочка дедуктивных умозаключений и т.д.
Этап закрепления доказательства в виде практического задания или упражнений, способствующих применению метода доказательства и запоминания её отдельных шагов.

По мере продвижения учащихся в изучении геометрии надобность в наводящих вопросах учителя уменьшается, а доля самостоятельности в отыскании способа доказательства, его построении, записи увеличивается.

Такой подход в работе с теоремой дает свои результаты, мотивируя тем самым учащихся на самостоятельное добывание знаний и желание преподнести их аудитории, включает учащихся к своего рода исследовательской работе по составлению и проведении работы над теоремой, доказательство над ним. А также воспитывает культуру общения, ответственность за принятие решений, стремление к самореализации, трудолюбие.

^ Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

I этап. Таблица № 3

№	^	Деятельность учащихся (ответы)
1.	Устно вслух читаем теорему и делаем разбор теоремы	По выбору учителя один ученик читает теорему остальные следят.
2.	Учитель задает наводящие вопросы: 1. В чем заключается основная мысль теоремы? 2. Как проводится перпендикуляр? 3. Что вам видится, если услышите слово перпендикуляр?	О проведении перпендикуляра С точки не лежащей на прямой проводится перпендикуляр к этой прямой отрезок.
3.	Теперь рассмотрим нашу теорему наглядно Карточка № 2 (приложение 2)	(учащиеся получают карточки)
4.	Теперь рассмотрим рисунки и определим: 1.Что означает рис №1 2. Что означает рис №2 3. Что означает рис № 3 4. Почему отрезок выделен красным цветом?	Данную точку Данную прямую Из данной точки, не лежащей на данную прямую опущен перпендикуляр на данную прямую. Потому что он перпендикуляр.

II этап. Таблица № 4

№	^	Деятельность учащихся (ответы)
1	Теперь из нашей теоремы определим условие и заключение.	Условие: из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой Заключение: притом только один
2	Так как мы имеем теорему, то наша теорема должна иметь………….?	доказательство
3	Что мы должны доказать? И из чего мы должны исходить?	Исходя из заключения теоремы должны доказать, что из точки, не лежащей на прямой, можно провести только один перпендикуляр к этой прямой.
4	А как Вы думаете что для этого нам достаточно иметь?	По условию теоремы нам достаточно иметь прямую и точку не лежащую на этой прямой.

III этап. (учащиеся построение доказательства делают поэтапно, обязательно на отдельных листочках заранее подготовленным учителем)

1. Мы имеем точку А и прямую ВС, притом точка А не лежит на прямой ВС. Рис. 4.

2. Докажем, что из точки А можно провести перпендикуляр к прямой ВС.

2.1. Точку А соединим с точкой В и получим угол АВСРис. 5 От луча ВС отложим угол МВС равный углу АВС.

Рис.6

2.3. Так как углы АВС и МВС равны, то первый из них можно наложить на второй так, что стороны ВА и ВС первого угла совместятся со сторонами ВМ и ВС второго угла.

2.4. Для того чтобы наглядно увидеть, то, что угол АВС равен углу МВС мы, аккуратно вырезаем наш рисунок.

2.5. Теперь по прямой ВС перегибаем рисунок. При этом точка А наложится на некоторую точку А1 луча ВМ.

2.6. Соединяем точку А и точку А1.

2.7. При этом отрезок А А1 пересекает прямую ВС. Точку пересечения отмечаем буквой Н.

2.8. Отрезок АН и есть искомый перпендикуляр к прямой ВС.

2.9. Теперь еще раз перегибаем наш макет и мы увидим, что луч АН совместится с лучом Н А1, поэтому угол АНВ и угол А1НВ, следовательно угол АНВ равен углу А1НВ. При этом данные углы смежные, значит каждый из них прямой. Итак, отрезок АН перпендикулярен отрезку ВС.

Теперь докажем, что из точки А можно провести только один перпендикуляр к прямой ВС.

Рис.7

3.1. Если предположить, что через точку А можно провести еще один перпендикуляр АН1, к прямой ВС, то получим, что две прямые АН и АН1, перпендикулярные к прямой ВС, пересекаются.

Рис.8

3.2. Так как мы знаем из темы «Перпендикулярные прямые», что две прямые, перпендикулярные к третьей, не пересекаются, то через точку А

невозможно провести еще одну перпендикулярную прямую АН1 к ВС кроме прямой АН. Теорема доказана.

IV этап.

1.Раздаются заранее подготовленные карточки каждому учащемуся.

Рис.9

Задание:

Построить перпендикуляр к прямой АВ с точки О без чертежного угольника, транспортира и доказать устно.
Построить перпендикуляр равный данному перпендикуляру без помощи линейки (дается отдельно каждому ученику на карточках).

Рис.10

стр. 36 № 100

dopoln.ru

Какую аналогию использует репетитор по математике в обучении доказательствам. Геометрия 7 класс)

Как известно, доказательство любого утверждения в геометрии, как и вообще в математике, представляет из себя определенный набор логических переходов от одного факта (условия) к другому (заключению). Решение задачи можно сравнить с поиском тропинки, ведущей от начального математического объекта (равнобедренного треугольника, параллельных прямых или любого другого) к конечному (равенству углов, равенство отрезков, треугольников ...).

Может ли репетитор по математике развить в 7 классе у ученика способность создавать и описывать такие логические маршруты? Безусловно. Причем готовить почву для такого развития нужно с малых лет. В 5 классе в распоряжении репетитора имеются олимпиадные задачи. Их можно найти у меня на сайте. В 7 классе вместо олимпиадного материала репетитором используются типовые геометрические задачи на доказательство. И те и другие вызывают серьезные затруднения у рядового школьника и требуют акуратного и тонкого подхода к ним со стороны репетитора.

Главным препятствием на пути формирования логического аппарата у ученика 7 класса (при условии, что он хорошо знает содержание теорем) является существенное изменение (по сравнению с 5 — 6 классом) характера работы с математическими (в основном геометрическими) объектами. За время учебы в младшей школе школьник привыкает к тому, что все необходимое для решения задачи дается ему в условии. И все формулы всегда работают. Когда репетитор по математике в 7 классе впервые произносит слово «доказательство», то от прежнего постоянства мало что остается. Оказывается, что изучаемое не всегда можно использовать. Это обстоятельство оказывает влияние даже на бывших отличников, которые к середине 7 класса неожиданно для себя и родителей начинают приносить непривычно низкие оценки по геометрии.

Меняется стиль решения задач (теперь в них нужно постоянно что-то доказывать) и требования к их оформлению. Из-за того, что новые (виртуальные) формы лишены предметной привязки к реальным процессам (к измерениям и нахождениям) они труднее запоминаются. Ученик не может визуально соотнести (сравнить) происходящее в доказательстве с каким-нибудь близким и понятным действием или знакомым явлением. Отсюда и проблемы.

Многие репетиторы по математике строят разъяснительную работу исключительно на оформлении задач, объясняя логику действий записями. Однако далеко не всегда эти записи помогают пониманию геометрии как науки. Даже если репетитор использует систему классических сокращений (систему фраз, стрелок, знаков, объединяющих скобок и др.), методично повторяя их из урока в урок. К сожалению, математическая точность и лаконичности не всегда хватает для запуска «мозгового двигателя» ученика.

Мне доводилось сталкивался с ситуациями, когда в 7 классе репетитор по математике (по совместительству — школьный преподаватель) заставлял своего подопечного писать целые трактаты — сочинениями на тему «почему и отчего». Логику поиска маршрута решения ученик не видел и просто записывал в тетрадь под диктовку репетитора стандартные математические штампы и обороты. Писал и не только. Воспроизвести их в аналогичных ситуациях он не мог.

Большой объем записей при классическом оформлении мешает концентрироваться на построении самой сути доказательства — логической цепочки (дорожки, маршрута). Если репетитор по математике начинает расставлять ссылки на все используемые в доказательстве теоремы (или заполняет логические переходы формулировками теорем), то непременно мешают ученику выделить главную линию доказательства. Чтобы указать в оформлении факты, на которых основывается тот или иной логический вывод, репетитору приходится каждый раз их указывать. Это также мешает концентрироваться на главном, ибо значительно увеличивает объемы записей.

Длинное и путанное оформление доказательства получается даже при использовании классических сокращений. В результате репетитор по математике «теряет» ученика уже на втором-третьем выводе-переходе. Память и внимание в 7 классе работают крайне неустойчиво, поэтому преподавателю приходится постоянно возвращаться к одному и тому же. Это только вносит смуту в ход рассуждений.

Какую методику использует репетитор по математике для наилучшего восприятия техники доказательств? Важно значительно сократить количество записей. Это удается сделать только при работе с краткими схемами. Каждая такая схема составляется в процессе поиска доказательства и служит отличным средством для визуального контроля за происходящим. Она не является заменой оформлению и играет роль некой памятки или опорного черновика. Репетитор кладет ее перед глазами учащегося и заносит информацию обо всех основных этапах (узлах) доказательства. Что они из себя представляют и как в 7 классе можно заинтересовать доказательствами пойдет речь далее.

Как репетитор по математике снимает проблему понимания логики доказательства?

Одна из проблем, с которой постоянно сталкивается репетитор — неумение учеников искать решение, неумение думать. Для формирования навыка рассуждений с нуля, как мне кажется, нужны определенные организационные условия, построенные на сравнении доказательства с каким-нибудь простым и понятным реальным процессом. Если репетитор по математике этого не сделает, — возникнут сложности в объяснениях. Доказательство примет строгие математические формы, трудно воспринимаемые детьми. Возникнут проблемы с переключением внимания и, как следствие, увеличится вероятность обнуления «буфера» памяти. Репетиторы часто жалуются на это. В процесс размышлений над задачей ученики забывают о полученных ими же математических фактах. Докажут равенство углов и забудут про это. Или вообще забудут о том, что доказывает :).

Аналогия захвата города

Понимание доказательства требует полного визуального контроля за происходящим. Кроме этого нужна достаточно интересная и простая аналогия с реальностью. Что интересно ученику 7 класса? Он еще ребенок и, как правило, не вышедший из игрового возраста. Репетитор по математике просто обязан это использовать. Игровая форма деятельности в сочетании с точной аналогией дает великолепные результаты. Я сравниваю доказательство геометрического факта с проведением широкомасштабной военной операции (битвой, сражением, завоеванием), что составляет суть одной из самых популярных игр у подростков — игрой в стратегию.

Ставится цель — захватить вражеский город «В» (итог доказательства). Для этого у ученика имеются начальные ресурсы, сконцентрированные в городе «А» (это данные условия задачи). Математические факты (равенство углов, отрезков, наличия равнобедренного или прямоугольного треугольника и т.д.), используемые в ходе доказательства — условия для ведения боевых действий: военные базы, солдаты, оружие, танки, самолеты, ракеты, солярка, пули, снаряжение, противогазы и др. Изначально их недостаточно для завоевания «В». И нет дорог для продвижения воинских частей. Ее и нужно построить.

Известно, например, что имея танки, можно захватить город «С», который репетитор по математике ассоциирует с каким-либо логическим условием (ранее изученным математическим фактом). Пройденные ранее теоремы — дороги, ведущие от одного города к другому (этих городов между «А» и «В» — великое множество). Эти дороги построены, но попасть на них можно только проложив путь от города А.

Можно красиво описать ситуацию. Город «В» окружен лесом, болотом или иными трудно преодолимыми препятствиями, но к нему ведут дороги от других городов, через которые его можно захватить. О некоторых из них имеются данные разведки. Названия городов — это математические факты (равенство углов, треугольников, параллельность прямых, сумма односторонних углов, смежных углов и т.д.). Города могут быть соединены дорогой (если один из фактов является следствием другого), а могут быть и не соединены. Репетитор по математике предлагает ученику разработать план: построить маршрут от «А» к «В». Но как? Удар по «В» можно нанести из каких-то соседних городов (неких логических островков), которые нужно найти на карте. В самом деле, не можем же мы сразу ударить по городу «В» из штаба «А» (если это не ядерная война:)) ). Нарисуем (или представим себе) города, откуда ведут дороги к городу «В». Репетитор по математике намечает несколько пустых кружков вокруг будущего конца цепочки и просит ученика подумать о том, каким математическим содержанием их можно было бы заполнить. При определенной подготовительной работе репетитора над пониманием каждой теоремы в отдельности, ученик вполне способен перечислить имеющиеся варианты. Затем нужно подумать о том, захвачены ли эти островки (города) или нет. Возможно, в каком из них находятся части нашей армии или город напрямую соединен со штабом «А». (если дорога от «А» к «В» уже построена).

Если какой-то математический факт является следствием сразу нескольких условий (к городу ведут несколько дорог), то захватить его ресурсы можно только направив армейские подразделения сразу по всем таким дорогам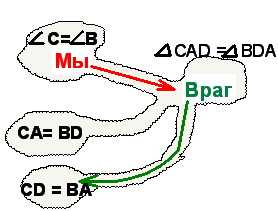 (иначе генералы вражеской армии вместе необходимым нам для продолжения войны ресурсами (продовольствием, снарядами, танками и др) просто уйдут от нас одной из них.

Знакомство с правилами игры «захват города» происходит гораздо быстрее, чем это может показаться по описанию. Репетитору достаточно показать одну-две задачи и ребенок уже погружен в процесс. Глаза горят, интересно. Если репетитор по математике хочет научить своего подопечного классическому методу поиска необходимых условий (решению от конца к началу), — то лучше всего навести ученика на эту идею при последовательном обсуждении двух стратегий составления плана операции:

1) Можно начать с разработки завершающего удара. Для этого (как описывалось выше) нужно найти город для нанесения непосредственного удара по «В» (смотрим, что необходимо знать, чтобы доказать ...).2) Тотальная стратегия боевых действий. Можно завоевывать все города подряд, начиная с «А». Репетитор по математике советует нарисовать как можно больше стрелок (дорог) от «А» к другим точкам на карте. Вторгаемся в какой-нибудь город и смотрим, пригодится ли он нам для дальнейшего или нет. Таким образом, репетитор по математике реализует формирование навыка поиска теорем, применимых в условии задачи вообще. Это крайне полезный навык. Если не удается понять, как подступится к доказываемому факту, нужно открыть (найти) хотя бы какой-нибудь дополнительный факт. Он может помочь в достижении цели.

Пример того, как подобную схему строит репетитор по математике — план завоевания города «В» (он выделен синим цветом):

Пример задачи по геометрии (7 класс): Рассмотрим типовую задачу по геометрии на доказательство параллельности двух прямых, взятую из материалов широко распространенного сборника «Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса» авторов А.П. Ершова и В.В Голобородько. Вариант В1 из работы С10. Условие задачи и рисунок Вы видите слева.

Схема репетитора к задаче (методика захвата города):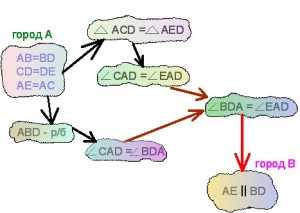Мы наносим удары по двум соседним городам и — равнобедренный. Затем захватываем города с углами. Части нашей армии с двух сторон наносят удар по городу и, наконец, попадают в город .

Колпаков А.Н. Репетитор по математике — Москва. Автор приема работы.

ankolpakov.ru

Как доказывать теорему?

Если в обычной жизни, для того чтобы на что-то указать, достаточно сказать: «Смотри!» и все сразу становится ясно, то в науке, любой факт, должен подтверждаться для того чтобы его признали. То же самое творится с теоремами в математике, ведь они являются недоказанными утверждениями. Они доказываются путем цепочки логических мышлений и с помощью аксиом, которые не ставятся под сомнение.

Итак, как нужно доказывать теорему? Теорему можно доказать путем логического мышления и выстраивания логической цепочки. Также применяются заранее доказанные теоремы и аксиомы. Все предельно просто, если включить логику и действовать по конкретному алгоритму доказывания теорем.

Каким правилам следовать в доказывание теоремы?

Нужно найти последовательность аксиом, теорем и т.д., которые могли бы помочь доказывать теорему. Следуя им нужно составить логичную цепочку.
Нет обязательных правил, которые помогли бы доказать теорему. Правила указывают возможное направление, которое поможет доказать теорему и носят название эвристические правила.
Объекты, о которых речь в теореме нужно заменить другими названиями и определениями, которые могли бы отражать его сущность и указать на конкретные характеристики объекта.
В случае сложной теоремы допускается разделение теоремы на части и доказательство каждой части по отдельности.
Доказывать теорему нужно в двух направлениях, от заключения к условиям и от условий к заключению.
Начиная доказывать теорему нужно идти с отрицанием того что нужно доказать, чтобы в итоге доказать что первоначальное предположение подтвердилось. Итак, начинать нужно со слов «предположим обратное», а в конце дойти до вывода, что «первоначальное подтверждение является верным».

Что касается практической части, с чего и следует начать, это создать графический чертеж теоремы. Для этого нужно создать две графы «Дано» и «Доказано». В первой графе записываете те факты, которые известны, а во второй, то, что следует доказать.

Заметка: если у вашего папы скоро днюха, самое время выбрать подарок отцу на день рождение (http://www.gift-for-man.ru/).

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru