Подготовка к олимпиаде по математике - 5 класс. Задания № 1. Как подготовить ребенка к олимпиаде по математике 5 класс
Подготовка к олимпиаде по математике
ЗАДАНИЯ № 1 (5-ый класс)
1.В день рождения дяди Федора почтальон Печкин хочет выяснить, сколько тому лет. Шарик говорит, что дяде Федору больше 11 лет, а кот Матроскин утверждает, что больше 10 лет. Сколько лет дяде Федору, если известно, что ровно один из них ошибся? Ответ обоснуйте.
Петя тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/70 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?
3. В примере на сложение двух чисел первое слагаемое меньше суммы на 2000, а сумма больше второго слагаемого на 6.
Восстановите пример.
Без ореха (от дупла до орешника) белка бежит со скоростью 4 м/сек, а с орехом (от орешника до дупла) — со скоростью 2 м/сек. На путь от дупла до орешника и обратно она тратит 54 секунды. Найдите расстояние от дупла до орешника. Ответ обоснуйте.
Цифры трёхзначного числа A записали в обратном порядке и получили число B. Может ли число, равное сумме A и B, записываться только нечётными цифрами?
У двузначного числа первая цифра вдвое больше второй. Если к этому числу прибавить квадрат его первой цифры, то получится квадрат некоторого целого числа. Найдите исходное двузначное число.
Петя и Вася участвовали в велогонке. Все участники стартовали одновременно и показали на финише различное время. Петя финишировал сразу после Васи и оказался на десятом месте. Сколько человек участвовало в гонке, если Вася был пятнадцатым с конца?
Однажды Миша, Витя и Коля заметили, что принесли в детский сад одинаковые игрушечные машинки. У Миши есть машинка с прицепом, есть маленькая машинка и есть зеленая машинка без прицепа. У Вити есть машинка без прицепа и маленькая зеленая с прицепом, а у Коли — большая машинка и маленькая синяя с прицепом. Машинку какого вида (по цвету, размеру и наличию прицепа) принесли мальчики в детский сад? Ответ объясните.
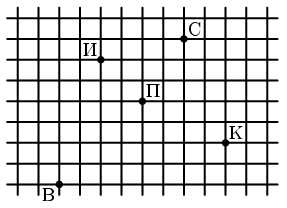
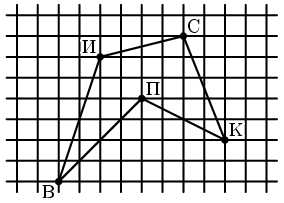
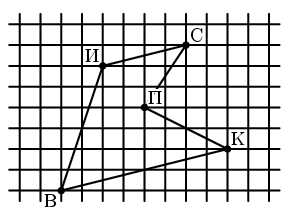
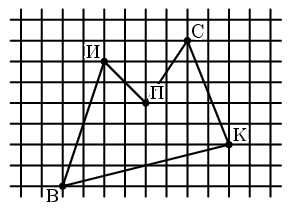
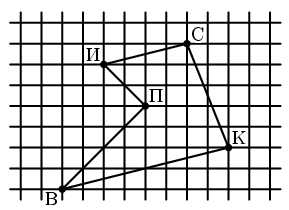
В точке В живет Винни-Пух, а в точках К, С, П и И – его друзья Кролик, Сова, Пятачок и ослик Иа-Иа (см. рисунок). Зимним утром Винни-Пух навестил их всех по одному разу, а потом вернулся домой. При этом он протоптал в снегу 5 прямых тропинок от домика к домику, не пересекающих друг друга. Начертите как можно больше возможных маршрутов Винни-Пуха.
Иван, Петр и Сидор ели конфеты. Их фамилии – Иванов, Петров и Сидоров. Иванов съел на 2 конфеты меньше Ивана, Петров – на 2 конфеты меньше Петра, а Петр съел больше всех. У кого из них какая фамилия?
РЕШЕНИЯ к ЗАДАНИЯМ №1:
Заметим, что если не ошибся Шарик, то не ошибся и Матроскин, что противоречит условию. Значит, Шарик сказал неправду, в отличие от кота Матроскина. Таким образом, дяде Федору больше 10 лет, но не меньше 11. Следовательно, дяде Федору исполнилось 11 лет.
Поскольку 1/5 + 1/6 > 1/3, то сумма данных дробей 1/3 + 1/5 + 1/6 + 1/70 + 1/3 > 1, что противоречит здравому смыслу.
Если из суммы двух чисел вычесть одно из слагаемых, то получится другое слагаемое. Из условия следует, что второе слагаемое равно 2000, а первое – 6.
Поскольку обратно белка бежит в два раза медленнее, то время, затраченное белкой на обратную дорогу, в два раза больше времени, которое она тратит на дорогу от дупла до орешника. Поэтому время, затраченное на дорогу от дупла до орешника, в три раза меньше времени, затраченного на всю дорогу, то есть равно 54 : 3 = 18 секунд. Следовательно, расстояние от дупла до орешника равно 18 * 4 = 72 метра.
Пусть, например, A = 219. Тогда B = 912, A + B = 1131.
Первая цифра в два раза больше второй только у следующих двузначных чисел: 21, 42, 63 и 84. Проверкой убеждаемся, что условию задачи удовлетворяет только число 21.
Так как Петя оказался на десятом месте, а Вася финишировал перед ним, то Вася занял девятое место. Вася был пятнадцатым с конца, значит за ним финишировало еще четырнадцать человек. Следовательно, в гонке участвовало 23 человека.
Если бы Коля принес синюю маленькую машинку с прицепом, то Витя должен был принести машинку с прицепом, но у Вити она зеленая. Значит, Коля принес большую машинку, а Витя не маленькую, то есть машинку без прицепа. Тогда Миша не мог принести машинку с прицепом, и не мог принести маленькую машинку. Значит, Миша должен был принести зеленую машинку без прицепа. Таким образом, каждый из мальчиков принес большую зеленую машинку без прицепа.
Иванов съел меньше Ивана, а Петр съел больше всех, значит, Петр – не Иванов. По той же причине Петр – не Петров, то есть фамилия Петра – Сидоров. Иванов – не Иван, значит, Иванова зовут Сидор. Следовательно, Петрова зовут Иван.
infourok.ru
Подготовка к олимпиадам 5-7 класс
Программа курса
«Обучение решению олимпиадных задач по математике» для 5-7 классов
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Математика – интегрированный учебный предмет, объединяющий в своем содержании числа и выражения, уравнения и неравенства, числовые функции, геометрические фигуры и измерение геометрических величин, элементы теории вероятностей и статистики в их взаимосвязи и взаимодействии.
Математика как никакой другой школьный предмет дает огромный простор для развития умственной деятельности учащихся, это та учебная дисциплина, которая расширяет кругозор учащихся, формирует мировоззрение, дает возможность раскрыть в учащихся способности в самых различных областях деятельности.
Умение решать задачи, особенно олимпиадные, всегда являлось одним из показателей математической одаренности ученика. Недаром многие вузы для победителей и призеров различного уровня олимпиад устанавливают льготы.
Данная программа поможет учителю систематизировать работу по подготовке учащихся к участию в олимпиадах и конкурсах различного уровня, окажет помощь в выявлении одаренных детей. В идеале подготовка школьников к олимпиадам должна начинаться в V-VII классах.
Устойчивый интерес к математике начинает формироваться в 14 -15 лет. Но это не происходит само собой: необходимо чтобы уже с 5 класса занятия математикой носили системный характер, особое внимание следует уделять тому, чтобы у учеников не возникла проблема потери интереса к математике.
Для того, чтобы ученик 5, 6 или 7 класса начал всерьез заниматься математикой, необходимо, чтобы на предыдущих этапах он почувствовал, что размышления над трудными, нестандартными задачами могут доставлять радость.
Цель программы
организовать работу с учащимися, имеющими повышенный интерес к изучению математики, включить учащихся в научно-познавательную и исследовательскую деятельность.
сформировать и развить у школьников такие качества, которые позволят им подходить к решению задач творчески, развить интуицию до уровня озарения.
воспитывать ученика как личность интеллектуально развитую, компетентную, успешную, адаптированную к современным реалиям жизни и востребованную обществом
Задачи:
интеллектуальное развитие учащихся, выявление и развитие математических способностей, формирование качеств мышления, характерных для математической деятельности;
формирование у учащихся устойчивого интереса к математике; овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности
углубленное изучение разделов школьной программы
расширение математического кругозора учащихся путем знакомства с методами решения олимпиадных задач и задач повышенной сложности;формирование представлений о математике как части общечеловеческой культуры, понимание значимости математики для общественного прогресса;
использование информационно-коммуникационных технологий для реализации новых способов и форм самообучения и саморазвития;формирование навыков перевода различных задач на язык математики
Данная программа опирается на следующие основные принципы отбора содержания учебного материала: научности, непрерывности образования, деятельности, внутрипредметной и межпредметной интеграции, доступности, учета индивидуальных достижений учащихся, принцип творчества.
Работа по обучению решению нестандартных задач предполагает применение педагогики, методики, психологии, личного творчества преподавателя.
Процесс изучения курса «Обучение решению олимпиадных задач» направлен на формирование у учащихся следующих компетенций:
владение культурой мышления, способностью к обобщению, анализу, постановке цели и выбору путей её достижения ,
применение методов математической обработки информации, теоретического и экспериментального исследования
способность логически верно выстраивать устную и письменную речь .
Работа с учащимися должна вестись по двум векторам: повышать эрудицию учащихся и обучать умению соединять знания в различных направлениях, для чего их, прежде всего, следует ознакомить с различными схемами мыслительного процесса.
Решение олимпиадных задач позволяет учащимся накапливать опыт в сопоставлении, наблюдении, думать и рассуждать, выявлять несложные математические закономерности, высказывать догадки, нуждающиеся в доказательстве. Формированию интеллектуальной компетенции способствует участие учащихся в математических олимпиадах и интеллектуальных конкурсах.
Предлагаемое тематическое разбиение данного курса предполагает творческое отношение к нему, последовательность тематических занятий, а также разбиение задач на параллели могут быть изменены в зависимости от индивидуальности каждого учащегося и всей группы, а также, если выясняется, что есть необходимость вернуться к какой-то ранее пройденной теме, либо включить в рассмотрение задачи другой темы, намеченной на более поздний срок. Необходимо постоянно возвращаться к уже решенным задачам предыдущих лет обучения и побуждать учащихся к потребности находить новые идеи и способы решений.
Курс рассчитан на три года, составлен на 102 часа (34 часа в год) и предназначен для учащихся 5 -7 классов.
Курс построен таким образом, чтобы учащийся смог подключиться к усвоению отдельных разделов курса в течение учебного года. Предпочтительны коллективные занятия, особенно эффективны занятия в малых группах.
Определение эффективности проведенных занятий
производится следующими способами:
выдача домашних заданий с последующими проверками, разборами задач;
проведение школьного тура республиканской олимпиады по математике с определением победителей;
участие в различных математических конкурсах, таких как международный математический конкурс «Кенгуру», «Акбота», Интернет олимпиады и т. д.
Формы подведения итогов усвоения данного курса:
Итоги реализации данного курса проводятся на основе анализа портфолио, в которое входят рейтинг результатов выполненных домашних заданий (в зависимости от объема и сложности), результаты участия в математических конкурсах «Кенгуру», «Акбота», дистанционных олимпиадах, в школьных олимпиадах и конкурсах, Интернет олимпиадах и т.д.
Лучшие ученики по итогам учебного года награждаются похвальными грамотами и могут быть направлены для отдыха в оздоровительные лагеря по линии «Дарын».
Данный курс обеспечен дидактическим материалом. Задачи собраны из разных источников, для решения которых необходимы знания, полученные в ходе изучения школьного курса математики.
II. СОДЕРЖАНИЕ УЧЕБНОГО МАТЕРИАЛА
Пятый класс
Арифметика (9 часов)
Секреты быстрого счета. Признаки делимости. Числовые неравенства и оценки. Дроби.
Геометрия (11 часов)
Задачи на разрезание, перекладывание и построение фигур, игра «Пифагор». Задачи с кубиками. Вычисление площадей фигур разбиением на части и дополнением.
Логика (14 часов)
Логические таблицы («лжецы» и «правдивые»). Переливания. Взвешивания. Решения «с конца». Задачи со спичками Популярные и классические логические задачи.
Игры: игры-шутки, решение и составление ребусов.
Шестой класс
Арифметика ( 6 часов)
Методы устного счета. Признаки делимости. Числовые ребусы. Делимость и остатки. Последняя цифра степени. Проценты. Десятичная система счисления. Числовые неравенства и оценки. Арифметические конструкции.
Геометрия (4 часа)
Задачи на разрезание, перекладывание и построение фигур. Вычисление площадей фигур разбиением на части и дополнением. Задачи на построение с идеей симметрии. Неравенство треугольника.
Логика (10 часов)
Задачи про рыцарей и лжецов Логические задачи, решаемые перебором (таблицей). Переливания. Взвешивания. Популярные и классические логические задачи.
Принцип Дирихле: принцип переполнения и не заполнения; доказательство от противного; конструирование «ящиков». Раскраски: шахматная раскраска; замощения. Игры: игры-шутки; выигрышные позиции; симметрия и копирование действий противника.
Алгебра и начала анализа (9 часов)
Четность: делимость на 2; чередования; парность. Разность квадратов: устный счет; задачи на экстремум. Задачи на совместную работу. Разные задачи на движение. Суммирование последовательностей: арифметическая прогрессия; геометрическая прогрессия со знаменателем 2 и ½.
Комбинаторика (5 часов)
Дерево вариантов Правило произведения и суммы. Факториал. Правило дополнения. Правило кратного подсчета.
Седьмой класс
Арифметика (4 часа)
Признаки делимости на 9 и 11. Делимость и остатки. Остатки квадратов. Разложение на простые множители. Неравенства в арифметике. Недесятичные системы счисления. Арифметические конструкции.
Геометрия (5 часов)
Задачи на перекладывание и построение фигур. Задачи на построение с идеей симметрии. Неравенство треугольника. Против большего угла лежит большая сторона. Вычисление площадей фигур разбиением на части и дополнением.
Логика (11 часов)
Популярные и классические логические задачи. Принцип Дирихле: доказательство от противного; конструирование «ящиков»; с дополнительными ограничениями; в связи с делимостью и остатками; разбиение на ячейки (например, на шахматной доске). Раскраски: виды раскрасок. Инварианты: четность; делимость; сумма; метод сужения объекта; правило крайнего.
Алгебра (2 часа)
Разность квадратов. Квадрат суммы, выделение полного квадрата. Разложение многочленов на множители: группировкой; по формулам сокращенного умножения.
Анализ (4 часа)
Разные задачи на движение. Суммирование последовательностей: арифметическая прогрессия; геометрическая прогрессия. Задачи на совместную работу.
Теория множеств (2 часа)
Булевы операции на множествах. Формула включений и исключений.
Комбинаторика (3 часа)
Правило произведения. Выборки с повторениями и без. Правило дополнения. Размещения и сочетания.
Графы (3 часа)
Четность и сумма ребер. Эйлеровы графы. Ориентированные графы.
III. ТРЕБОВАНИЯ К ЗНАНИЯМ, УМЕНИЯМ И НАВЫКАМ.
В процессе изучения курса учащиеся должны:
Иметь представление о структуре математики как науки, о сферах практического применения математических методов.
Знать основные понятия, термины и определения, используемые в математике.
Уметь работать с теорией – это значит находить ее в различных источниках, быстро ориентироваться в ней, использовать основные правила работы с литературой для нахождения нужного материала;
Уметь использовать математические модели для формализации задач.
Освоить различные методы и приемы решения олимпиадных задач различного характера. уметь применять нестандартные методы решения комбинаторных, арифметических задач.
Уметь сочетать различные звенья знаний, чтобы получить множество гипотез решения задачи (синтез)
Уметь устанавливать связи в разных направлениях мыслительного процесса, проще говоря, подойти к решению проблемы с разных сторон. Владеть дедуктивным и индуктивным методами построения логических рассуждений в процессе решения задач.
Расширять свой кругозор, пополнять знания, чтобы, в конечном счете, владеть материалом по всем разделам математики.
V. ОСОБЕННОСТИ МЕТОДИЧЕСКОЙ СИСТЕМЫ ОБУЧЕНИЯ РЕШЕНИЮ ОЛИМПИАДНЫХ ЗАДАЧ
Для успешного обучения учащихся решению олимпиадных задач с самого начала необходимо настроить учеников на успех, обратить внимание на формирование «веры в себя», привлечение учеников для участия в любых конкурсах, соревнованиях, состязаниях.
Начиная уже с пятого класса, особое внимание следует уделять тому, чтобы у учеников не возникла проблема потери интереса к математике. Для решения проблемы развивать математическое мышление школьника требуется в трех основных направлениях: арифметическом, пространственно-геометрическом и логическом.
Необходима постоянная работа над улучшением устного счета, овладением различными его приемами, постоянно решаются задачи, развивающие пространственное воображение и расширяющие геометрический кругозор. Классические и занимательные логические задачи направлены на развитие способности к рассуждениям.
На всех занятиях в качестве разминки следует выполнять арифметические упражнения устного счета, используя для этого различные тренажеры. Учащиеся должны уверенно знать не только таблицу умножения чисел первого десятка, но и степени чисел 2 и 3 (хотя бы до ста), усвоить, что такое простое число, помнить первые несколько простых чисел (хотя бы из первых трех десятков) и уметь раскладывать на простые составные числа (например, 12, 36, 56, 75). Школьников следует научить пользоваться признаками делимости (в десятичной системе счисления, пока без доказательства) на 2, 4, 5, 3 и 9, а также решать задачи на делимость с числами 6, 15, 45 и т.д.
Серьезное внимание следует уделять решению логических задач, так как такие задачи требуют от учащихся выявления из предложенных «жизненных обстоятельств» математической сущности задачи, т.е. создания математической модели., что постоянно приходится делать в задачах по комбинаторике, теории графов, на составление алгебраических уравнений и т. д.
Для развития пространственного воображения хорошо подходят задачи на подсчет количества геометрических фигур в сложных рисунках; на вычисления площадей многоугольников, изображенных на клетчатой бумаге, игра «Пифагор»; различные конструктивные задачи, в т.ч. задачи со спичками.
Начиная с шестого класса, можно приступать к работе над основными темами логико-комбинаторного цикла: принцип Дирихле, основные принципы комбинаторики, идея четности, задачи-игры, метод раскрасок, идея симметрии и др., не забывая о тематике пятого класса.
Для шестого класса арифметическая «разминка» столь же желательна, как и для пятого. Надо добиться того, чтобы школьники выучили квадраты второго десятка, степени двойки и тройки примерно до тысячи (не сразу, конечно; для этих целей полезно иногда проводить «диктанты» на знание этих чисел). Следует показать им формулу «разности квадратов» и научить с ее помощью устно выполнять умножение.
В седьмом классе до изучения в геометрии основных фактов и теорем на строгом, чисто формальном уровне полезно эти факты изложить без доказательства, опираясь на геометрическую иллюстративность и интуицию, и приступить к решению содержательных геометрических задач.
Следует обратить внимание на необходимость изучения специальных идей и подходов к нахождению решений, переходить от технически простых, модельных задач к задачам с хорошо замаскированными идеями, необычностью или «неожиданностью» их присутствия в решении.
V. ПРИМЕРНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА
5 класс
№п/п
Тема занятия
Кол-во
часов
I.
Арифметика
9
1
Секреты быстрого счета
3
2
Признаки делимости
2
3
Числовые неравенства и оценки
2
4
Дроби. Решение задач.
2
II.
Геометрия
11
1
Задачи на разрезание, перекладывание и построение фигур
3
2
Игра «Пифагор».
3
3
Задачи с кубиками
2
4
Вычисление площадей фигур разбиением на части и дополнением
3
III.
Логика
14
1
Логические таблицы («лжецы» и «правдивые»).
2
2
Переливания. Взвешивания
2
3
Решения «с конца».
2
4
Задачи со спичками
2
5
Популярные и классические логические задачи.
2
6
Игры: игры-шутки
2
7
Решение и составление ребусов
2
итого
34
6 класс
№п/п
Тема занятия
Кол-во
часов
I.
Арифметика
6
1
Методы устного счета
1
2
Признаки делимости. Делимость и остатки. Последняя цифра степени.
1
3
Числовые ребусы
1
4
Проценты.
1
5
Десятичная система счисления.
1
6
Числовые неравенства и оценки. Арифметические конструкции
1
II.
Геометрия
4
1
Задачи на разрезание, перекладывание и построение фигур
1
2
Вычисление площадей фигур разбиением на части и дополнением
1
3
Задачи на построение с идеей симметрии. Неравенство треугольника.
1
4
Задачи на построение с идеей симметрии. Неравенство треугольника.
1
III.
Логика
10
1
Задачи про рыцарей и лжецов
1
2
Логические задачи, решаемые перебором (таблицей).
1
3
Популярные и классические логические задачи.
1
4
Переливания. Взвешивания
1
5
Принцип Дирихле: принцип переполнения и не заполнения; доказательство от противного; конструирование «ящиков».
3
6
Раскраски: шахматная раскраска; замощения.
2
7
Игры: игры-шутки, выигрышные позиции; симметрия и копирование действий противника.
1
IV.
Алгебра и начала анализа
9
1
Четность: делимость на 2; чередования; парность.
1
2
Разность квадратов: устный счет; задачи на экстремум
1
3
Задачи на совместную работу.
2
4
Разные задачи на движение
2
5
Суммирование последовательностей.
1
6
Арифметическая прогрессия;
1
7
Геометрическая прогрессия со знаменателем 2 и ½.
1
V.
Комбинаторика
5
1
Дерево вариантов
1
2
Правило произведения и суммы.
1
3
Факториал.
1
4
Правило дополнения
1
5
Правило кратного подсчета.
1
итого
34
7 класс
№п/п
Тема занятия
Кол-во
часов
I.
Арифметика
4
1
Признаки делимости на 9 и 11. Делимость и остатки. Остатки квадратов.
1
2
Разложение на простые множители.
1
3
Неравенства в арифметике.
1
4
Недесятичные системы счисления. Арифметические конструкции.
1
II.
Геометрия
5
1
Задачи на перекладывание и построение фигур.
1
2
Задачи на построение с идеей симметрии.
1
3
Неравенство треугольника. Против большего угла лежит большая сторона
2
4
Вычисление площадей фигур разбиением на части и дополнением
1
III.
Логика
11
1
Популярные и классические логические задачи
1
2
Принцип Дирихле: доказательство от противного; конструирование «ящиков»
1
3
Принцип Дирихле: с дополнительными ограничениями
2
4
Принцип Дирихле: в связи с делимостью и остатками
2
5
Принцип Дирихле: разбиение на ячейки
2
6
Раскраски: виды раскрасок.
1
7
Инварианты: четность; делимость; сумма; метод сужения объекта; правило крайнего.
2
IV.
Алгебра
2
1
Разность квадратов. Квадрат суммы, выделение полного квадрата.
1
2
Разложение многочленов на множители: группировкой; по формулам сокращенного умножения.
1
V.
Анализ
4
1
Разные задачи на движение.
1
2
Суммирование последовательностей: арифметическая прогрессия; геометрическая прогрессия.
2
3
Задачи на совместную работу.
1
VI.
Теория множеств
2
1
Булевы операции на множествах.
1
2
Формула включений и исключений.
1
VII.
Комбинаторика
3
1
Правило произведения. Выборки с повторениями и без.
1
2
Правило дополнения. Размещения и сочетания.
1
3
Размещения и сочетания.
1
VIII.
Графы
3
1
Четность и сумма ребер.
1
2
Эйлеровы графы.
1
3
Ориентированные графы.
1
итого
34
Литература.
1 Дрозина В.В., Дильман В.Л. Механизм творчества решения нестандартных задач: руководство для тех, кто хочет научиться решать нестандартные задачи: учеб. пособие /В.В., Дрозина, В.Л. Дильман. – Челябинск: Изд-во Чел. гос. пед. ун-та, 2007. – 211с.
2. Кордемский Б. А., Ахадов А.А. Удивительный мир чисел. Москва «Просвещение», 1986.
3. Бабинская И.Л. Задачи математических олимпиад /И.Л. Бабинская. – М.: Наука, 1975. – 112с.
4. Все задачи «Кенгуру» /сост. Т.А. Братусь, Н.А. Жарковская, А.И. Плоткин и др. – СПб.: Ин-т продуктивного обучения, 2003. – 146с.
5. Головоломки для детей и взрослых /сост. И.Н. Кириченко. – Донецк: ИКФ «Сталкер», 1997. – 496с.
6. Казакова Е.Е. Математический кружок 5 и 6 классов /Е.Е. Казакова. – Челябинск: Изд-во ФМЛ, 2000. – 52с.
7. Козлова Е.Г. Сказки и подсказки. Задачи для математического кружка /Е.Г. Козлова. – М.: Изд-во МЦНМО, 2004. – 165с.
8. Кордемский Б.А. Математическая смекалка /Б.А. Кордемский. – М.: Гос.издат. технико-теоретической литературы, 1957. – 575с.
9. Кордемский Б.А., Ахадов А.А. Удивительный мир чисел (Математические головоломки и задачи для любознательных): кн. для учащихся /Б.А. Кордемский, А.А. Ахадов. – М.: Просвещение, 1986. – 144с.
10. Мерзляков А.С. Принцип Дирихле. Факультативный курс /А.С. Мерзляков. – Ижевск: Изд-во НПЦ «Бизнес-старт», 1993. – 87с.
11. Перельман Я.И. Занимательная арифметика. Загадки и диковинки в мире чисел /Я.И. Перельман. – М.: Изд-во Русанова, 1994.
12. Пойа Д. Как решать задачу /Д. Пойа. Львов: Журн. "Квантор", 1991. – 215с.
13. Сборник задач московских математических олимпиад: пособие для внеклассной работы по математике /сост. А.А. Леман. – М.: Просвещение, 1965. – 384с.
14. Шарыгин И.Ф., Шевкин А.В. Математика: задачи на смекалку: учеб.пособие для 5 – 6 классов общеобразовательных учреждений /И.Ф. Шарыгин, А.В. Шевкин. – М.: Просвещение, 1995. – 80с.
15. НестеренкоЮ., Олехник С., Потапов М. Лучшие задачи на смекалку. Москва, «АСТ-ПРЕСС», 1999.
16. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. Москва «Просвещение», 1984.
17. Перельман Я.И. Живая математика. Москва,1994. АО «Столетие».
18. Перельман Я.И. Математические рассказы и головоломки. Домодедово. ВАП-VAP, 1994.
multiurok.ru
Олимпиада по математике для 5 класса. Школьный этап.
1.Расставьте в записи 7 х9+12:3-2 скобки так,чтобы значение получившегося выражения было равно 23. (5 баллов)
Ответ:(7х9+2):3-2=23.
2.В один сосуд входит 3 л,а в другой-5л. Как с помощью этих сосудов налить в кувшин 4л воды из водопроводного крана (10 баллов)
Ответ: Наполняем сосуд в 5л и отливаем в трехлитровый сосуд.Оставшиеся 2 литра переливаем в кувшин.Повторяя эту операцию, наливаем в кувшин 4 л воды.
3.В оранжерее были срезаны гвоздики: белых и розовых-400 штук,розовых и красных-300,белых и красных-440.Сколько гвоздик каждого цвета было срезано в оранжерее
( 15 баллов )
Ответ:Белых-270, розовых-130, красных-170.Сложить все данные числа и разделить результат на два; получим количество гвоздик всех трех цветов,срезанных в оранжерее.
4.Когда отцу было 27 лет, то сыну было только 3 года,а сейчас сыну в три раза меньше лет,чем отцу.Сколько лет сейчас каждому из них (15 баллов)
Ответ: Пусть сейчас сыну-х лет, тогда отцу-3х лет.Поскольку разность возрастов отца и сына постоянна и равна по условию 24 годам,то имеем уравнение:3х-х=24, откуда х=12; 3х=36
5.Принесли 5 чемоданов и 5 ключей от этих чемоданов,но неизвестно,какой ключ от какого чемодана.Сколько проб придется сделать в самом худшем случае,чтобы подобрать к каждому чемодану свой ключ (25 баллов)
Ответ: Первым из ключей,которые мы будем подбирать к чемодану,в самом худшем случае придется сделать 4 пробы.(Если ключ не подошел к 4 чемоданам из 5,значит, он соответствует пятому).Вторым ключом в самом худшем случае сделаем 3 пробы и т д.Всего потребуется 10 проб (4+3+2+1=10
6.Рыбак поймал рыбу.Когда у него спросили, колько весит пойманная рыба,он сказал: «Я думаю,что ее хвост весит 1 кг,голова весит столько, сколько хвост и половина туловища, а туловище- сколько голова и хвост вместе.»Сколько же весит рыба (30 баллов)
Ответ:По условию туловище рыбы весит 1 кг ( вес хвоста) плюс вес головы,а так как вес головы равен 1 кг (вес хвоста) и половине туловища,то получается, что туловище рыбы весит 2 кг плюс половина туловища, т.е. туловище весит 4 кг.Тогда голова весит 3 кг (сколько хвост и половина туловища),а вся рыба-8 кг (3+4+1=8)
Просмотр содержимого документа
«Олимпиада по математике для 5 класса. Школьный этап. »
Первый всероссийский (школьный) этап олимпиады по математике 5 класс.
1.Расставьте в записи 7 х9+12:3-2 скобки так,чтобы значение получившегося выражения было равно 23. (5 баллов)
Ответ:(7х9+2):3-2=23.
2.В один сосуд входит 3 л,а в другой-5л. Как с помощью этих сосудов налить в кувшин 4л воды из водопроводного крана (10 баллов)
Ответ: Наполняем сосуд в 5л и отливаем в трехлитровый сосуд.Оставшиеся 2 литра переливаем в кувшин.Повторяя эту операцию, наливаем в кувшин 4 л воды.
3.В оранжерее были срезаны гвоздики: белых и розовых-400 штук,розовых и красных-300,белых и красных-440.Сколько гвоздик каждого цвета было срезано в оранжерее
( 15 баллов )
Ответ:Белых-270, розовых-130, красных-170.Сложить все данные числа и разделить результат на два; получим количество гвоздик всех трех цветов,срезанных в оранжерее.
4.Когда отцу было 27 лет, то сыну было только 3 года,а сейчас сыну в три раза меньше лет ,чем отцу.Сколько лет сейчас каждому из них (15 баллов)
Ответ: Пусть сейчас сыну-х лет, тогда отцу-3х лет.Поскольку разность возрастов отца и сына постоянна и равна по условию 24 годам,то имеем уравнение:3х-х=24, откуда х=12; 3х=36
5.Принесли 5 чемоданов и 5 ключей от этих чемоданов,но неизвестно,какой ключ от какого чемодана.Сколько проб придется сделать в самом худшем случае,чтобы подобрать к каждому чемодану свой ключ (25 баллов)
Ответ: Первым из ключей,которые мы будем подбирать к чемодану,в самом худшем случае придется сделать 4 пробы.(Если ключ не подошел к 4 чемоданам из 5,значит, он соответствует пятому).Вторым ключом в самом худшем случае сделаем 3 пробы и т д.Всего потребуется 10 проб (4+3+2+1=10
6.Рыбак поймал рыбу.Когда у него спросили, колько весит пойманная рыба,он сказал: «Я думаю,что ее хвост весит 1 кг,голова весит столько, сколько хвост и половина туловища, а туловище- сколько голова и хвост вместе.»Сколько же весит рыба (30 баллов)
Ответ:По условию туловище рыбы весит 1 кг ( вес хвоста) плюс вес головы,а так как вес головы равен 1 кг (вес хвоста) и половине туловища,то получается, что туловище рыбы весит 2 кг плюс половина туловища, т.е. туловище весит 4 кг .Тогда голова весит 3 кг (сколько хвост и половина туловища),а вся рыба-8 кг (3+4+1=8)
kopilkaurokov.ru
Подготовка учащихся к олимпиадам по математике
ПОДГОТОВКА УЧАЩИХСЯ К ОЛИМПИАДАМ ПО МАТЕМАТИКЕ
Статья
«Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научится этому можно, только беря пример с наилучших образцов и постоянно практикуясь. Но помните: если вы хотите научиться плавать, то смелее входите в воду, а если хотите научиться решать задачи, то решайте их».
Д.Пойа
Умение решать задачи, особенно олимпиадные, всегда являлось одним из показателей математической одаренности ученика.
Тем более что сегодня часто по итогам олимпиад оценивают итоги внеклассной и внешкольной работы по математике в школе, районе.
Подготовка учащегося к участию в олимпиаде – труд не одного года. Нужно отметить, что успешно участвовать в предметной олимпиаде может учащийся, знакомый со стандартными приемами решения задач, выходящих за рамки школьного курса. Определенную роль играет и скорость мышления учащегося. Целесообразно начинать подготовку «олимпиадников» в 5-7 классах. Только при таком подходе учащийся, попавший на олимпиаду в 8-9 классах, будет чувствовать себя уверенно: скажется опыт решения нестандартных задач, накопленный за несколько лет.
В ходе проведения занятий обращаю внимание на то, чтобы: занятия проходили в форме живого, непосредственного общения школьников и преподавателя, учитывался индивидуальный подход; обучающиеся овладели умениями общего учебного характера, разнообразными способами деятельности и приобрели опыт:
- решения разнообразных задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
- исследовательской деятельности, проведения экспериментов;
- точного, грамотного изложения своих мыслей в устной и письменной речи;
- поиска, систематизации, анализа, классификации информации, использования разнообразных информационных источников.
Необходимо подчеркнуть, что подготовка и проведение занятий – творческий процесс.
Из своего многолетнего опыта работы хочу предложить несколько советов:
- не заниматься с учениками одной темой в течение продолжительного промежутка времени. Даже в рамках одного занятия полезно сменить направление деятельности;
- постоянно возвращаться к пройденному материалу. Это можно делать, предлагая задачи на данную тему в устных и письменных олимпиадах и других соревнованиях;
- при разборе темы выделяю несколько основных логических вех и добиваюсь безусловного понимания этих моментов;
- постоянно обращаюсь к нестандартным и «спортивным» формам проведения занятий, не забывая при этом подробно разобрать все предложенные на них задачи. Также использую на занятиях развлекательные и шуточные задачи.
При непосредственной подготовке учащихся к математическим конкурсам и олимпиадам необходимо акцентировать внимание учащихся на следующих моментах:
- в качестве одной из задач конкурса любого уровня может быть задача, в условии которой фигурирует год проведения конкурса, олимпиады;
- как правило, в числе конкурсных задач отсутствуют задачи с длительными выкладками, на использование трудно запоминающихся формул, на использование справочных таблиц;
- если в условии требуется указать все возможные способы решения задачи, то от полноты количества указанных способов зависит и количество полученных баллов;
- если в условии задачи фигурирует вопрос «Можно ли...?», то для того чтобы доказать, что «можно» достаточно привести всего один положительный пример, а для того чтобы ответить, что «нельзя», необходимо рассмотреть все возможные случаи, обобщая их в стройное доказательство;
- всегда помнить, что задания составляются компетентными специалистами, и «некорректных формулировок условий задач», как правило, в конкурсных вариантах не встречается, а непонятные и непривычные формулировки как раз и характеризуются категорией нестандартности задачи.
Рекомендации учителю по подготовке учащихся:
- усилить подготовку учащихся по внепрограммному материалу;
- каждому учителю, прежде чем готовить учащегося к конкурсу, олимпиаде по математике, выработать педагогическую систему подготовки;
- использовать возможности кружковой работы, факультативных занятий по математике для подготовки к решению конкурсных, олимпиадных задач;
- отбор задач необходимо начать заблаговременно.
Приведу несколько возможных тем занятий для учащихся разных классов:
1. Задачи, решаемые с конца (5 – 6 кл.).
2. Занимательные задачи на проценты (6 кл.).
3. Математические ребусы (5 – 7 кл.).
4. Геометрические задачи со спичками (5 – 6 кл.).
5. Задачи на разрезание и перекрашивания фигур (5 – 7 кл.).
6. Графы (6 – 9 кл.).
7. Упражнения на быстрый счет (5 – 8 кл.).
8. Четность (7 – 9 кл.)
9. Делимость и остатки (7 – 9 кл.).
10. Занимательные задачи на построения (7 – 8 кл.).
11. Геометрические построения с различными чертежными инструментами (7 – 8 кл.).
12. Взвешивания (5 – 7 кл.).
13. Логические задачи (5 – 8 кл.).
14. Уравнения в целых и натуральных числах (7 – 11 кл.).
15. Геометрические задачи на местности (8 – 9 кл.).
16. Метод математической индукции (8 – 11 кл.).
17. Принцип Дирихле (6 – 9 кл.).
18. Текстовые задачи (7 - 9 кл.).
19. Уравнения, неравенства и их системы (7 – 11 кл.).
20. Доказательства неравенств (9 – 11 кл.).
21. Занимательные комбинаторные задачи (7 – 9 кл.).
22. Построение графика сложной функции (9 – 11 кл.).
23. Тригонометрические преобразования (10 – 11 кл.).
24. Планиметрия (7 – 9 кл.).
25. Стереометрия (10 – 11 кл.).
26. Некоторые примеры решения уравнений высших степеней ( 10-11кл.)
Проведение олимпиад и подготовка к ним через математические кружки, факультативные занятия и часы для дополнительной работы по математике должны привлекать детей своей индивидуальностью и интересными методами их проведения.
Роль учителя в этом деле огромная. В первую очередь учитель обязан создать благоприятные условия для того, чтобы ученик смог постигать новое в интересующей его науке. С помощью знаний учителя, умением методически правильно поставить перед учеником задачу посильную ученику, он добьется успеха.
Использованная литература:
1. Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. – К.,1994. – С.4.
2. Григорьева Г.И. подготовка школьников к олимпиадам по математике: 5 – 6 классы. – М.: Издательство « Глобус», 2009. – С.4 – 6.
3. Севрюков П.Ф. Школа решения олимпиадных задач по математике. – М. : Ставрополь , 2013. – С. 7 – 11.
4. Фарков А.В. Математические кружки в школе. 5 – 8 классы. – М.: Айрис – пресс, 2008. – С. 6.
5.Фарков А.В. Математические олимпиады: методика подготовки. 5 – 8 классы. – М.:ВАКО, 2014. – С.3 – 21.
videouroki.net
Вариант олимпиады по математике для 5 класса. Ремейк репетитора
Ученики продолжают приносить мне реальные варианты различных олимпиад. За последние несколько лет работы репетитором по математике я успел собрать приличную коллекцию олимпиадного материала для учащихся 4 — 5 классов. Ориентируюсь на нее при составлении плана урока. Толстенная пачка листов с тщательно отобранными и сортированными задачами (занимательными, нестандартными или логическими) занимает в моем шкафу целую полку. Перед тем, как свежий вариант дополнит ее оригинальными номерами, он проходит полную и обязательную проверку на корректность всех условий и формулировок, а также на соответствие решений программным стандартам по каждому классу.
Вниманию репетиторов по математике предлагается редактированная версия прошедшей в январе 2012 годаолимпиады для 5 класса от творческой лаборатории 2×2. Если Вы в ней участвовали, то заметите, что я несколько исправил тексты условий (убрал из них лишнее) и доработал вопросы. Один из номеров (про автобус с лжецами и правдолюбами) не прошел ОТК из-за своей неоднозначности и был заменен на 100% корректную задачу про цифры и квадраты. Приятного размышления!
Олимпиадные задачи по математике 5 класс
1) Преподаватель написал на доске число 2014 и предложил ученикам 5 класса «A» такую игру: за один ход можно или уменьшить или увеличить это число на произведение любых его цифр (в любом количестве). Нужно из 2014 за наименьшее число ходов получить 2047. Вася был победителем математической олимпиады и сразу догадался, что это сделать невозможно. Как он пришел к такому выводу?
2) Два листа прямоугольной формы наложили друг на друга как это показано на рисунке. Оказалось, что длина отрезка, выделенного синим цветом, равна 10см. Определите, какая площадь больше: «двойная» (закрашенная) или оставшаяся (из четырех треугольников взятых по одному разу) .
3) Взрослые и дети встали в круг. Известно, что у семерых человек оба соседа – дети, а у еще четверых один сосед взрослый, а другой — ребенок. Сколько всего детей встало в круг? Какое наименьшее число взрослых может быть при таком условии?
4) 
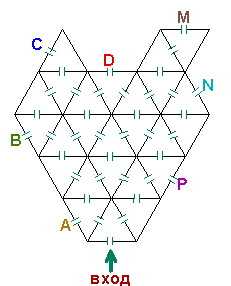Принцесса прогуливалась по замку. Она вошла в него через главные ворота, а вышла через какую-то из потайных дверей A,B,C,D,M, N или P. Двери обозначены на плане замка. Известно, что принцесса побывала в 15 комнатах ровно по одному разу. Через какие двери она могла выйти? Укажите все возможные варианты и объясните, почему она не могла выйти из замка через другие ворота.
5) 9 пустых кружков образуют квадрат 3×3. Расставьте в них цифры 1,2,3,4,5,6,7,8,9 так, чтобы их сумма во всех шести квадратах, показанных на рисунке, была одинаковой.
Комментарий репетитора по математике к №5: кажется, что с пятой задачей можно справиться только путем случайного подбора варианта (угадыванием) или перебирая все возможные расстановки цифр. Ни то ни другое не приветствуется. За угадывание могут вообще ни одного балла не поставить, а перебор выливается в такую рутину, что ни на одно из оставшихся заданий времени не хватит. Репетитор по математике должен научить ребенка отбрасывать значительное количество неподходящих вариантов, доводя их остаток до минимума. А уже по нему организовывать перебор. Для сокращения вариантов расстановки девяти цифр найдите сумму . С ее помощью определяется сумма трех цифр каждого из углов большого квадрата и варианты для центрального числа! Далее следует перебор.
О задаче про замок: Лучшая задача данной олимпиады. Обратите внимание на ориентацию треугольников в замке и попытайтесь объяснить такой факт: путь от одной комнаты до другой (измеренный промежуточными комнатами) всегда оказывается одной и той же четности. Это самое главное, что необходимо найти для завершения поиска решения.
Колпаков А.Н. Репетитор по математике — помощь в подготовке к олимпиадам. Москва.
Метки: Варианты олимпиад по математике
ankolpakov.ru
Смирнова Татьяна Ивановна - Подготовка к олимпиаде 5 класс
Департамент образования г. Москвы
Московский институт открытого образования
Примерные задания школьного тура математической олимпиады
5 класс
1. Сколько всего трехзначных чисел?
2. Календарь представляет собой два кубика, у каждого кубика на всех гранях написано по цифре. Дату (день месяца) составляют, используя один или два кубика. Придумайте, как написать цифры на кубиках, чтобы можно было получить любую дату от 1 до 31. (В ответе напишите, какие цифры должны быть на одном кубике, а какие – на другом.)
3. Разрежьте фигуру на рисунке справа на 4 равные части.
4. Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. А когда поезд отъезжал, один из них насчитал еще 2 скамейки. Сколько насчитали остальные?
5. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?
6. Мальчик Сережа увидел двоих двухголовых дракончиков, головы которых спутались. Драконы бывают либо правдивые, т.е. обе головы говорят только правду, либо лживые, т.е. обе головы всегда лгут. Сережа решил помочь дракончикам распутать головы. Но для этого ему надо знать, где чья голова. Он спросил это у дракончиков, на что головы ответили:
первая: «я – правдивая голова»;вторая: «третья голова – моя родная голова»;третья: «вторая голова – не родная мне голова»;четвертая: «третья голова – лживая».
Какие головы принадлежат каким дракончикам?
5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс
stimul56.ucoz.ru
Школьный портал для учителей и учеников
На прямой взяли 4 точки. Сколько всего получилось отрезков, концами которых являются эти точки? (2 балла)
Ответ: Всего получилось 6 отрезков.
Винни-Пуху подарили в день рождения бочонок с мёдом массой 7кг. Когда Винни-Пух сьел половину мёда, то бочонок с оставшимся мёдом стал иметь массу 4кг. Сколько килограммов мёда было первоначально в бочонке? (3 балла)
Ответ: В бочонке первоначально было 6кг мёда.
Решение: Оставшаяся половина мёда в бочонке имеет массу
7-4=3(кг). Значит, всего мёда 3*2=6(кг).
Сумма трех чисел равна их произведению. Эти числа различные и однозначные. Найти эти числа. (3 балла)
Ответ: 1,2,3.
Решение: 1+2+3=1*2*3
Турист поднимался в гору 5 часов, проходя каждый час 3 км. На обратном пути он увеличил скорость на 2 км/ч. Сколько часов потребовалось туристу на обратный путь? (3 балла)
Ответ: Туристу на обратный путь понадобилось 3 часа.
Решение: 5*3=15(км) — весь путь
3+2=5(км/ч) — скорость на обратном пути
15:5=3(ч) – время, потраченное на обратный путь
С хозяйством попа справляются 10работников. Каждый работник в день съедает каравай хлеба и другие продукты. Поп принял на работу Балду.
Живет Балда в поповом доме,
Спит себе на соломе,
Ест за четверых,
Работает за семерых.
Поп прогнал лишних работников. Сколько караваев хлеба экономил поп ежедневно? (2 балла)
Ответ: Поп ежедневно экономил три каравая.
Решение: Балда работал за семерых, а ел за четверых. Экономия составляет
7- 4=3(каравая)
По дереву ползет гусеница. За день она поднимается на 6 метров, а ночью опускается на 4 метра. За сколько дней она доползет до вершины, если высота дерева 14 метров?
Ответ: За 5 дней
Решение: В последний день гусеница поднимется на 6 метров, значит ей надо проползти ещё 14-6=8(м). В день она поднимается на 6-4=2(м). Тогда 8 метров проползет за 8:2=4 (дня). Все время движения составит 1+4=5 (дней)
Требуется распилить бревно на 6 частей. Каждый распил занимает 2 минуты. Сколько времени потребуется на эту работу?
Ответ: 10 минут
Решение: Распилов будет 5. Затраченное время 5*2=10 (мин)
shkola-zanyatij.ru
