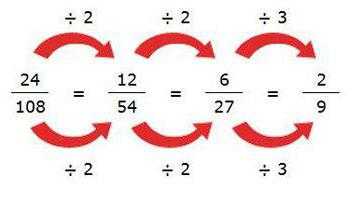
Как сократить дробь? Правила на все ситуации. Как объяснить ребенку сокращение дробей 6 класс
Правила сокращения дробей с примерами
Дети в школе учат правила сокращения дробей в 6 классе. В этой статье мы сначала расскажем вам о том, что же означает это действие, затем разъясним, как сократимую дробь перевести в несократимую. Следующим пунктом будут правила сокращения дробей, а затем уже постепенно подберемся к примерам.
Что значит "сократить дробь "?
Итак, все мы знаем, что обычные дроби делятся на две группы: сократимые и несократимые. Уже по названиям можно понять, что те, что сократимые - сокращаются, а те, которые несократимые - не сокращаются.
- Сократить дробь - это значит разделить ее знаменатель и числитель на их (отличный от единицы) положительный делитель. В результате, конечно, выходит новая дробь с меньшим знаменателем и числителем. Полученная дробь будет равна исходной дроби.
Стоит отметить, что в книгах по математике с заданием "сократите дробь " это значит, что нужно исходную дробь привести именно к этому несократимому виду. Если говорить простыми словами, то деление знаменателя и числителя на их наибольший общий делитель и есть сокращение.
Как сократить дробь. Правила сокращения дробей (6 класс)
Итак, здесь всего два правила.
- Первое правило сокращения дробей: сначала нужно будет найти наибольший общий делитель знаменателя и числителя вашей дроби.
- Второе правило: делить знаменатель и числитель на наибольший общий делитель, в конечном итоге получить несократимую дробь.
Как сократить неправильную дробь?
Правила сокращения дробей идентичны правилам сокращения неправильных дробей.
Для того чтобы сократить неправильную дробь, для начала нужно будет расписать на простые множители знаменатель и числитель, а уже потом общие множители сокращать.
Сокращение смешанных дробей
Правила сокращения дробей также распространяется на сокращение смешанных дробей. Есть лишь небольшая разница: целую часть мы можем не трогать, а дробную сократить или смешанную дробь перевести в неправильную, затем сократить и опять перевести в правильную дробь.
Сократить смешанные дроби можно двумя способами.
Первый: расписать дробную часть на простые множители и целую часть тогда не трогать.
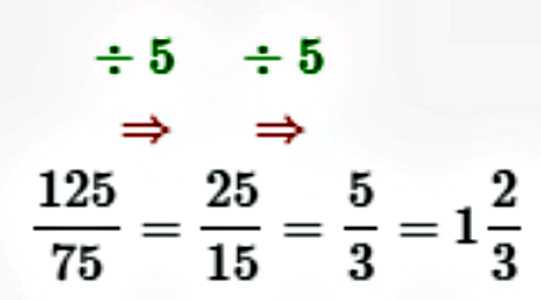
Второй способ: перевести сначала в неправильную дробь, расписать на обычные множители, потом сократить дробь. Уже полученную неправильную дробь перевести в правильную.
Примеры можно увидеть на фото выше.
Мы очень надеемся, что смогли помочь вам и вашим детям. Ведь на уроках они очень часто бывают невнимательными, поэтому приходится заниматься интенсивнее на дому самостоятельно.
fb.ru
6 класс. Математика. Сокращение дробей - Сокращение дробей
Комментарии преподавателя
Представьте себе такую ситуацию.
За столом 3 человека и 5 яблок. Делятся 5 яблок на троих. Каждому достается по яблока.
А за соседним столом еще 3 человека и тоже 5 яблок. Каждому опять по .
При этом всего 10 яблок и 6 человек. Каждому по .
Но это одно и то же.
. Эти дроби эквивалентны.
Можно увеличить в два раза количество людей и в два раза количество яблок. Результат будет тем же самым.
В математике это формулируется так:
Если числитель и знаменатель дроби умножить или разделить на одно и то же число (не равное 0), то новая дробь будет равна исходной.
Это свойство иногда называют «основным свойством дроби».
Примеры эквивалентных дробей
1. Путь от города до деревни – 7 км.
Мы идем по дороге и определяем пройденный путь по километровым столбикам. Пройдя три столбика, три километра, мы понимаем, что прошли пути.
Но если мы не видим столбиков (может, их не установили), можно путь считать по электрическим столбам вдоль дороги. Их 20 штук на каждый километр. То есть всего 140 на всем пути. Три километра – столбов. То есть мы прошли 60 из 140 столбов, .
2. Дробь на координатной плоскости можно отмечать точкой. Чтобы изобразить дробь отметим точку с координатой 3 по оси и 4 по оси . Проведем прямую из начала координат через нашу точку.
На этой же прямой будет лежать и точка, соответствующая дроби .
Они являются эквивалентными: (см. Рис. 1)
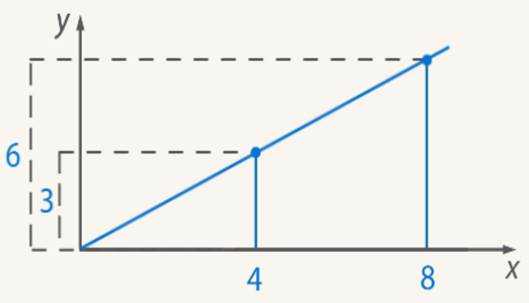
Рис. 1. Иллюстрация к примеру
3. На рисунке 2 два дома. Первый – высотой 6 метров и шириной 4, а второй – высотой 12 метров и шириной 8. Размеры разные, но дома по форме похожи. У них одинаковые пропорции, одинаковое отношение высоты к ширине.
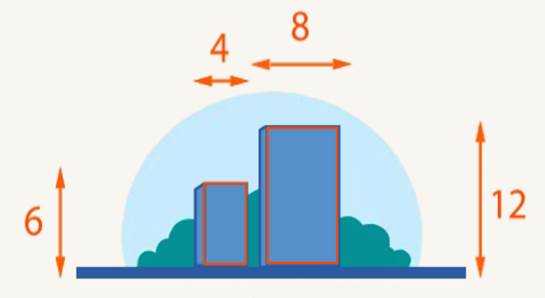
Рис. 2. Иллюстрация к примеру
Дробь можно было получить из умножением числителя и знаменателя на 4:
или из умножением на 2:
Но точно так же можно и вернуться назад.
У дроби можно числитель и знаменатель разделить на 2, получить :
Или числитель и знаменатель разделить на 4, получить :
Вот такой переход от одной дроби к другой с помощью деления числителя и знаменателя на одно и то же число называетсясокращением дроби.
У дроби можно разделить числитель и знаменатель на 100. Получим .
Это эквивалентная запись, но она короче. Мы сократили запись. Сократили дробь:
Посмотрим еще раз на цепочку эквивалентных дробей.
Дробь можно сократить на 2 и получить или сократить на 4 и получить .
Дробь нам не получится сократить до или , зато легко сократить на 5 и получить .
Только одну дробь из представленных мы не можем сократить: .
Такая дробь называется несократимой. Ее нельзя сократить.
Остальные сократимые. Их можно сократить.
Рассмотрим дробь .
Чтобы понять, можно ли ее сократить, нужно узнать, существует ли число, на которое делится и числитель, и знаменатель, есть ли общий делитель.
42 делится на 2, но 273 на 2 не делится.
42 делится на 3 (сумма цифр 6 делится на 3), и 273 делится на три (сумма цифр 12).
Значит, мы можем поделить числитель и знаменатель на 3, сократить дробь на 3.
Можно ли сократить полученную дробь дальше?
14 делится на 2 и на 7.
91 не делится на 2, но на 7 делится.
Значит, дробь можно сократить на 7.
Для чисел 2 и 13 нам уже не найти общего делителя.
Дробь несократима.
Не всегда легко, глядя на дробь, понять, можно ее сократить или нет.
Что нам может помочь в этом?
Чтобы сократить дробь, нужно найти общий делитель для числителя и знаменателя.
Но делители числа и его множители – это одно и то же.
2 и 5 – это множители, но на них можно разделить. Поэтому они же и делители.
То есть разложение на множители – это и разложение на делители.
Вернемся к нашему примеру.
Если бы числитель и знаменатель были разложены на множители, мы бы сразу поняли, как сократить дробь.
Общие множители (делители) – 3 и 7. На них и сокращаем.
Сократить дробь, разложив на множители числитель и знаменатель.
Разложим 60 на множители:
Разложим 126 на множители:
Сократим на общие множители, на 2 и на 3. Больше общих множителей (делителей) нет. Перемножим оставшиеся множители:
В школе 4 первых класса, и в каждом учится 27 учеников.
Есть 12 коробок мандаринов, в каждой по 45 штук. Сколько каждому первокласснику достанется мандаринов, если их поделить поровну?
Понятно, что надо количество мандаринов разделить на количество первоклассников.
Найдем и то и другое.
первоклассников.
мандаринов.
Осталось разделить.
мандаринов на первоклассника.
Но можно было и упростить себе задачу, ведь у нас уже было разложение на множители:
Не будем сразу считать, сколько мандаринов и сколько учеников. Сначала сократим нашу дробь. 12 и 4 делятся на 4. 3 и 27 делятся на 3.
Это решение оказалось проще.
Сейчас самостоятельно сократите следующие дроби:
Проверка:
Докажите, что дробь несократима:
Проверка:
разложим на простые множители числитель и знаменатель:
Общих множителей (общих делителей) нет. Значит, сократить невозможно. Дробь несократима.
Такие числа, как 220 и 273, не имеющие общих делителей, кроме 1, мы называем взаимно простыми.
То есть можно сказать про несократимую дробь следующее: дробь несократима, если ее числитель и знаменатель – взаимно простые числа.
Подведем итог.
- Сократить дробь – означает разделить ее числитель и знаменатель на одно и то же число (не равное нулю). В результате получаем равную (эквивалентную) дробь, но с меньшими числителем и знаменателем.
- Чтобы сократить дробь, нужно последовательно проверять, на что делятся числитель и знаменатель. Если находятся общий делитель, то на него и сокращать.
- Если разложить числитель и знаменатель на множители, то это упростит сокращение.
Всегда ли нужно сокращать?
Фраза: «Цена выросла на 20 %» буквально означает «цена выросла на », так как .
Дробь можно сократить. Получится .
Мы могли бы сказать: «цена выросла на ».
Это, конечно, то же самое. Но общая договоренность – говорить в процентах. Поэтому удобнее оставить эту величину в процентах, не сокращая дробь.
Сокращение – это инструмент. Но мы не обязаны его применять, если не считаем, что так станет проще.
источник конспекта - http://internetur
www.kursoteka.ru
6 класс. Математика. Сокращение дробей - Сокращение дробей
Комментарии преподавателя
Представьте себе такую ситуацию.
За столом 3 человека и 5 яблок. Делятся 5 яблок на троих. Каждому достается по яблока.
А за соседним столом еще 3 человека и тоже 5 яблок. Каждому опять по .
При этом всего 10 яблок и 6 человек. Каждому по .
Но это одно и то же.
. Эти дроби эквивалентны.
Можно увеличить в два раза количество людей и в два раза количество яблок. Результат будет тем же самым.
В математике это формулируется так:
Если числитель и знаменатель дроби умножить или разделить на одно и то же число (не равное 0), то новая дробь будет равна исходной.
Это свойство иногда называют «основным свойством дроби».
Примеры эквивалентных дробей
1. Путь от города до деревни – 7 км.
Мы идем по дороге и определяем пройденный путь по километровым столбикам. Пройдя три столбика, три километра, мы понимаем, что прошли пути.
Но если мы не видим столбиков (может, их не установили), можно путь считать по электрическим столбам вдоль дороги. Их 20 штук на каждый километр. То есть всего 140 на всем пути. Три километра – столбов. То есть мы прошли 60 из 140 столбов, .
2. Дробь на координатной плоскости можно отмечать точкой. Чтобы изобразить дробь отметим точку с координатой 3 по оси и 4 по оси . Проведем прямую из начала координат через нашу точку.
На этой же прямой будет лежать и точка, соответствующая дроби .
Они являются эквивалентными: (см. Рис. 1)

Рис. 1. Иллюстрация к примеру
3. На рисунке 2 два дома. Первый – высотой 6 метров и шириной 4, а второй – высотой 12 метров и шириной 8. Размеры разные, но дома по форме похожи. У них одинаковые пропорции, одинаковое отношение высоты к ширине.

Рис. 2. Иллюстрация к примеру
Дробь можно было получить из умножением числителя и знаменателя на 4:
или из умножением на 2:
Но точно так же можно и вернуться назад.
У дроби можно числитель и знаменатель разделить на 2, получить :
Или числитель и знаменатель разделить на 4, получить :
Вот такой переход от одной дроби к другой с помощью деления числителя и знаменателя на одно и то же число называетсясокращением дроби.
У дроби можно разделить числитель и знаменатель на 100. Получим .
Это эквивалентная запись, но она короче. Мы сократили запись. Сократили дробь:
Посмотрим еще раз на цепочку эквивалентных дробей.
Дробь можно сократить на 2 и получить или сократить на 4 и получить .
Дробь нам не получится сократить до или , зато легко сократить на 5 и получить .
Только одну дробь из представленных мы не можем сократить: .
Такая дробь называется несократимой. Ее нельзя сократить.
Остальные сократимые. Их можно сократить.
Рассмотрим дробь .
Чтобы понять, можно ли ее сократить, нужно узнать, существует ли число, на которое делится и числитель, и знаменатель, есть ли общий делитель.
42 делится на 2, но 273 на 2 не делится.
42 делится на 3 (сумма цифр 6 делится на 3), и 273 делится на три (сумма цифр 12).
Значит, мы можем поделить числитель и знаменатель на 3, сократить дробь на 3.
Можно ли сократить полученную дробь дальше?
14 делится на 2 и на 7.
91 не делится на 2, но на 7 делится.
Значит, дробь можно сократить на 7.
Для чисел 2 и 13 нам уже не найти общего делителя.
Дробь несократима.
Не всегда легко, глядя на дробь, понять, можно ее сократить или нет.
Что нам может помочь в этом?
Чтобы сократить дробь, нужно найти общий делитель для числителя и знаменателя.
Но делители числа и его множители – это одно и то же.
2 и 5 – это множители, но на них можно разделить. Поэтому они же и делители.
То есть разложение на множители – это и разложение на делители.
Вернемся к нашему примеру.
Если бы числитель и знаменатель были разложены на множители, мы бы сразу поняли, как сократить дробь.
Общие множители (делители) – 3 и 7. На них и сокращаем.
Сократить дробь, разложив на множители числитель и знаменатель.
Разложим 60 на множители:
Разложим 126 на множители:
Сократим на общие множители, на 2 и на 3. Больше общих множителей (делителей) нет. Перемножим оставшиеся множители:
В школе 4 первых класса, и в каждом учится 27 учеников.
Есть 12 коробок мандаринов, в каждой по 45 штук. Сколько каждому первокласснику достанется мандаринов, если их поделить поровну?
Понятно, что надо количество мандаринов разделить на количество первоклассников.
Найдем и то и другое.
первоклассников.
мандаринов.
Осталось разделить.
мандаринов на первоклассника.
Но можно было и упростить себе задачу, ведь у нас уже было разложение на множители:
Не будем сразу считать, сколько мандаринов и сколько учеников. Сначала сократим нашу дробь. 12 и 4 делятся на 4. 3 и 27 делятся на 3.
Это решение оказалось проще.
Сейчас самостоятельно сократите следующие дроби:
Проверка:
Докажите, что дробь несократима:
Проверка:
разложим на простые множители числитель и знаменатель:
Общих множителей (общих делителей) нет. Значит, сократить невозможно. Дробь несократима.
Такие числа, как 220 и 273, не имеющие общих делителей, кроме 1, мы называем взаимно простыми.
То есть можно сказать про несократимую дробь следующее: дробь несократима, если ее числитель и знаменатель – взаимно простые числа.
Подведем итог.
- Сократить дробь – означает разделить ее числитель и знаменатель на одно и то же число (не равное нулю). В результате получаем равную (эквивалентную) дробь, но с меньшими числителем и знаменателем.
- Чтобы сократить дробь, нужно последовательно проверять, на что делятся числитель и знаменатель. Если находятся общий делитель, то на него и сокращать.
- Если разложить числитель и знаменатель на множители, то это упростит сокращение.
Всегда ли нужно сокращать?
Фраза: «Цена выросла на 20 %» буквально означает «цена выросла на », так как .
Дробь можно сократить. Получится .
Мы могли бы сказать: «цена выросла на ».
Это, конечно, то же самое. Но общая договоренность – говорить в процентах. Поэтому удобнее оставить эту величину в процентах, не сокращая дробь.
Сокращение – это инструмент. Но мы не обязаны его применять, если не считаем, что так станет проще.
источник конспекта - http://interneturok.ru/ru/school/matematika/6-k
www.kursoteka.ru
Сокращение дробей. Что значит сократите дробь?
Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.
Сокращение дробей, определение и формула.
Что такое сокращение дробей? Что значит сократить дробь?
Определение:Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно основному свойству рациональных чисел.
Формула сокращения дробей основного свойства рациональных чисел.
\(\frac{p \times n}{q \times n}=\frac{p}{q}\) Рассмотрим пример:Сократите дробь \(\frac{9}{15}\)
Решение:Мы можем разложить дробь на простые множители и сократить общие множители.
\(\frac{9}{15}=\frac{3 \times 3}{5 \times 3}=\frac{3}{5} \times \color{red} {\frac{3}{3}}=\frac{3}{5} \times 1=\frac{3}{5}\) Ответ: после сокращения получили дробь \(\frac{3}{5}\). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.
\(\frac{9}{15}=\frac{3}{5}\) Как сокращать дроби? Сокращение дроби до несократимого вида.
Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.
Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.
Получите несократимую дробь \(\frac{48}{136}\).
Решение:Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.48=2⋅2⋅2⋅2⋅3136=2⋅2⋅2⋅17НОД(48, 136)= 2⋅2⋅2=6
\(\frac{48}{136}=\frac{\color{red} {2 \times 2 \times 2} \times 2 \times 3}{\color{red} {2 \times 2 \times 2} \times 17}=\frac{\color{red} {6} \times 2 \times 3}{\color{red} {6} \times 17}=\frac{2 \times 3}{17}=\frac{6}{17}\) Ответ: \(\frac{6}{17}\) несократимая дробь.
Правило сокращения дроби до несократимого вида.
- Нужно найти наибольший общий делитель для числители и знаменателя.
- Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.
Пример:Сократите дробь \(\frac{152}{168}\).
Решение:Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.152=2⋅2⋅2⋅19168=2⋅2⋅2⋅3⋅7НОД(152, 168)= 2⋅2⋅2=6
\(\frac{152}{168}=\frac{\color{red} {6} \times 19}{\color{red} {6} \times 21}=\frac{19}{21}\) Ответ: \(\frac{19}{21}\) несократимая дробь.
Сокращение неправильной дроби.
Как сократить неправильную дробь?Правила сокращения дробей для правильных и неправильных дробей одинаковы.
Рассмотрим пример:Сократите неправильную дробь \(\frac{44}{32}\).
Решение:Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.
\(\frac{44}{32}=\frac{\color{red} {2 \times 2 } \times 11}{\color{red} {2 \times 2 } \times 2 \times 2 \times 2}=\frac{11}{2 \times 2 \times 2}=\frac{11}{8}\) Сокращение смешанных дробей.
Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.
Рассмотрим пример:Сократите смешанную дробь \(2\frac{30}{45}\).
Решение:Решим двумя способами:Первый способ:Распишем дробную часть на простые множители, а целую часть не будем трогать.
\(2\frac{30}{45}=2\frac{2 \times \color{red} {5 \times 3}}{3 \times \color{red} {5 \times 3}}=2\frac{2}{3}\) Второй способ:Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.
\(2\frac{30}{45}=\frac{45 \times 2 + 30}{45}=\frac{120}{45}=\frac{2 \times \color{red} {5 \times 3} \times 2 \times 2}{3 \times \color{red} {3 \times 5}}=\frac{2 \times 2 \times 2}{3}=\frac{8}{3}=2\frac{2}{3}\) Вопросы по теме:Можно ли сокращать дроби при сложении или вычитании?Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:
Вычислите выражение \(\frac{50+20-10}{20}\) .
Решение:Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.
\(\frac{50+\color{red} {20}-10}{\color{red} {20}}=\frac{60}{20}=\frac{3 \times 20}{20}=\frac{3}{1}=3\) На какие числа можно сокращать дробь?Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac{100}{150}\).
Распишем на простые множители числа 100 и 150.100=2⋅2⋅5⋅5150=2⋅5⋅5⋅3Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50
\(\frac{100}{150}=\frac{2 \times 50}{3 \times 50}=\frac{2}{3}\) Получили несократимую дробь \(\frac{2}{3}\).
Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac{100}{150}\) на 2.
\(\frac{100}{150}=\frac{2 \times 50}{2 \times 75}=\frac{50}{75}\) Получили сократимую дробь \(\frac{50}{75}\).
Какие дроби можно сокращать?Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac{4}{8}\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.
Пример:Сравните две дроби \(\frac{2}{3}\) и \(\frac{8}{12}\).
Эти две дроби равны. Рассмотрим подробно дробь \(\frac{8}{12}\):
\(\frac{8}{12}=\frac{2 \times 4}{3 \times 4}=\frac{2}{3} \times \frac{4}{4}=\frac{2}{3} \times 1=\frac{2}{3}\) Отсюда получаем, \(\frac{8}{12}=\frac{2}{3}\)
Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.
Пример:Сократите если возможно следующие дроби: а) \(\frac{90}{65}\) б) \(\frac{27}{63}\) в) \(\frac{17}{100}\) г) \(\frac{100}{250}\)
Решение:а) \(\frac{90}{65}=\frac{2 \times \color{red} {5} \times 3 \times 3}{\color{red} {5} \times 13}=\frac{2 \times 3 \times 3}{13}=\frac{18}{13}\)б) \(\frac{27}{63}=\frac{\color{red} {3 \times 3} \times 3}{\color{red} {3 \times 3} \times 7}=\frac{3}{7}\)в) \(\frac{17}{100}\) несократимая дробьг) \(\frac{100}{250}=\frac{\color{red} {2 \times 5 \times 5} \times 2}{\color{red} {2 \times 5 \times 5} \times 5}=\frac{2}{5}\)
tutomath.ru
Сокращение дробей
Сокращение дробей. Вот и добрались до сокращения. Применяется здесь основное свойство дроби. НО! Не всё так просто. Со многими дробями (в том числе из школьного курса) вполне можно им обойтись. А если взять дроби «покруче»? Разберём подробнее! Рекомендую посмотреть весь список материалов с дробями.
Итак, мы уже знаем, что числитель и знаменатель дроби можно умножать и делить на одно и тоже число, дробь от этого не изменится. Рассмотрим три подхода:
Подход первый.
Для сокращения делят числитель и знаменатель на общий делитель. Рассмотрим примеры:
Сократим:
В приведенных примерах мы сразу видим какие взять делители для сокращения. Процесс несложен – мы перебираем 2,3.4,5 и так далее. В большинстве примеров школьного курса этого вполне достаточно. А вот если будет дробь:
Тут процесс с подбором делителей может затянуться надолго ;). Конечно, такие примеры лежат вне школьного курса, но справляться с ними нужно уметь. Чуть ниже рассмотрим как это делается. А пока вернёмся к процессу сокращения.
Как рассмотрено выше, для того чтобы сократить дробь, мы осуществляли деление на определённый нами общий делитель(ли). Всё правильно! Стоит лишь добавить признаки делимости чисел:
— если число чётное то оно делится на 2.
— если число из последних двух цифр делится на 4, то и само число делится на 4.
— если сумма цифр из которых состоит число делится на 3, то и само число делится на 3. Например 125031, 1+2+5+0+3+1=12. Двенадцать делится на 3, значит и 123031 делится на 3.
— если в конце числа стоит 5 или 0, то число делится на 5.
— если сумма цифр из которых состоит число делится на 9, то и само число делится на 9. Например 625032 =.> 6+2+5+0+3+2=18. Восемнадцать делится на 9, значит и 623032 делится на 9.
Второй подход.
Если кратко суть, то на самом деле всё действо сводится к разложению числителя и знаменателя на множители и далее к сокращению равных множителей в числителе и знаменателе (данный подход – это следствие из первого подхода):
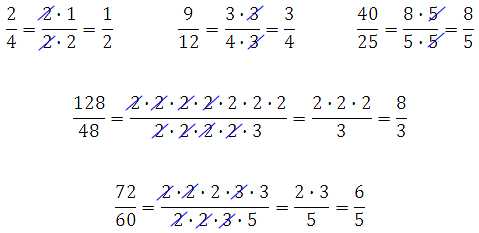
Визуально, чтобы не запутаться и не ошибиться равные множители просто перечёркивают. Вопрос – а как разложить число на множители? Нужно определить перебором все делители. Это тема отдельная, она несложная, посмотрите информацию в учебнике или интернете. Никаких великих проблем с разложением на множители чисел, которые присутствуют в дробях школьного курса, вы не встретите.
Формально принцип сокращения можно записать так:
Подход третий.
Тут самое интересное для продвинутых и тех, кто хочет им стать. Сократим дробь 143/273. Попробуйте сами! Ну и как, быстро получилось? А теперь смотрите!
Переворачиваем её (числитель и знаменатель меняем местами). Делим уголком полученную дробь переводим в смешанное число, то есть выделяем целую часть:
Уже проще. Мы видим, что числитель и знаменатель можно сократить на 13:
Далее переводим дробь в обыкновенную:
А теперь не забываем снова перевернуть дробь обратно, давайте запишем всю цепочку:
Проверено – времени уходит меньше, чем на перебор и проверку делителей. Вернёмся к нашим двум примерам:
Первый. Делим уголком (не на калькуляторе), получим:
Эта дробь попроще конечно, но с сокращением опять проблема. Теперь отдельно разбираем дробь 1273/1463, переворачиваем её:
Тут уже проще. Можем рассмотреть такой делитель как 19. Остальные не подходят, это видно: 190:19= 10, 1273:19 = 67. Ура! Запишем:
Теперь записываем исходное число:
Следующий пример. Сократим 88179/2717.
Делим, получим:
Отдельно разбираем дробь 1235/2717, переворачиваем её:
Можем рассмотреть такой делитель как 13 (до 13 не подходят):
Числитель 247:13=19 Знаменатель 1235:13=95
*В процессе увидели ещё один делитель равный 19. Получается, что:
Теперь записываем исходное число:
И не важно, что будет больше в дроби – числитель или знаменатель, если знаменатель, то переворачиваем и действуем как описано. Таким образом мы можем сократить любую дробь, третий подход можно назвать универсальным.
Конечно, два примера рассмотренные выше это непростые примеры. Давайте попробуем эту технологию на уже рассмотренных нами «несложных» дробях:
Две четвёртых.
Знаменатель меньше числителя. Переворачиваем и делим:
Девять двенадцатых. Переворачиваем:
Соток двадцать пятых. Числитель больше знаменателя, переворачивать не нужно:
Сто двадцать восемь сорок восьмых. Числитель больше знаменателя, переворачивать не нужно:
Семьдесят две шестидесятых. Числитель больше знаменателя, переворачивать не нужно:
Разумеется, третий подход применили к таким простым примерам просто как альтернативу. Способ, как уже сказано, универсальный, но не для всех дробей удобный и корректный, особенно это относится к простым.
Многообразие дробей велико. Важно, чтобы вы усвоили именно принципы. Строгого правила по работе с дробями просто нет. Посмотрели, прикинули каким образом удобнее действовать и вперёд. С практикой придёт навык и будете щёлкать их как семечки.
Вывод:
Если видите общий(ие) делитель(и) для числителя и знаменателя, то используйте их для сокращения.
Если умеете быстро раскладывать на множители число, то разложите числитель и знаменатель, далее сокращайте.
Если никак не можете определить общий делитель, то воспользуйтесь третьим подходом.
*Для сокращения дробей важно усвоить принципы сокращения, понимать основное свойство дроби, знать подходы к решению, быть крайне внимательным при вычислениях.
И запомните! Дробь принято сокращать до упора, то есть сокращать её пока есть общий делитель.
C уважением, Александр Крутицких.
Делитель информацией в социальных сетях
matematikalegko.ru
Как сократить дробь | Алгебра
Как сократить алгебраическую (рациональную) дробь, числитель и знаменатель которой содержат выражения, которые отличаются только знаками?
Например, как сократить дробь
Для начала вспомним, как от выражения (a-b) перейти к выражению (b-a). Для этого нужно вынести «минус» за скобки (при этом все знаки слагаемых в скобках изменятся на противоположные):
В дроби вынести «минус» за скобки можно или в числителе, или в знаменателе. По свойству алгебраических дробей, знак «минус» можно вынести перед дробью:
В данном примере числитель и знаменатель дроби сокращаем на (a-b):
Рассмотрим другие примеры сокращения алгебраических дробей такого вида.
Сокращать можно только множители!
В числителе и знаменателе дроби — многочлены. Чтобы сократить дробь, надо разложить многочлены на множители. В числителе есть общий множитель 2b, в знаменателе — a. Вынесем их за скобки:
Выражения, стоящие в скобках в числителе и в знаменателе, отличаются только знаками. Вынесем знак «минус» перед дробью, например, из знаменателя (при этом все знаки слагаемых, стоящих в скобках, изменятся на противоположные):
После чего сокращаем дробь на общий делитель (2a-b).
В числителе выносим общий множитель 2 за скобки, знаменатель раскладываем по формуле разности квадратов:
Вынесем «минус» перед дробью, например, из числителя:
Сокращаем дробь на (m-7).
В числителе — 4 слагаемых. Группируем первое слагаемое со вторым, третье — с четвертым. В знаменателе выносим общий множитель 6 за скобки:
В числителе выносим общие множители за скобки: из первых скобок — y, из вторых — -2, затем — (x-3):
Сокращаем дробь на (x-3):
Если после сокращения перед дробью остался «минус», а в числителе или знаменателе есть разность, «минус» надо внести в разность (при этом знаки слагаемых изменятся на противоположные). Вносим «-» в числитель, -(y-2)=2-y:
Соответственно,
То есть, чтобы сменить знаки слагаемых в квадрате разности, «минус» за скобки (и перед дробью) выносить не нужно. Это верно не только для квадрата разности, но и для любой другой четной степени:
В случае возведения разности в нечетную степень при смене знаков слагаемых знак «минус» за скобки выносить нужно:
Примеры.
В числителе — полный квадрат разности, в знаменателе — разность квадратов. Раскладываем на множители:
Удобнее изменить знаки слагаемых вверху, поскольку при этом не нужно изменять знак перед дробью:
Сокращаем дробь на (10y-9x):
Вынесем знак «минус» перед дробью, например, из знаменателя:
Сокращаем на (b-4)³:
Сокращение дробей в алгебре — важная составляющая часть сложения, вычитания, умножения и деления алгебраических дробей. Упрощать рациональные выражения приходится при решении уравнений, неравенств, задач и т.д.
Далее мы будем рассматривать действия над алгебраическими дробями.
www.algebraclass.ru
Как сократить дробь? Правила на все ситуации :: SYL.ru
Без знания того, как сократить дробь, и наличия устойчивого навыка в решении подобных примеров очень непросто изучать в школе алгебру. Чем дальше, тем больше на базовые знания о сокращении обыкновенных дробей накладывается новой информации. Сначала появляются степени, потом множители, которые позже становятся многочленами.
Как тут не запутаться? Основательно закреплять умения в предыдущих темах и постепенно готовиться к знаниям о том, как сократить дробь, усложняющуюся год от года.
Базовые знания
Без них не удастся справиться с заданиями любого уровня. Чтобы понять, как сократить дробь, нужно уяснить два простых момента. Первый: сокращать можно только множители. Этот нюанс оказывается очень важным при появлении многочленов в числителе или знаменателе. Тогда нужно четко различать, где находится множитель, а где стоит слагаемое.
Второй момент говорит о том, что любое число можно представить в виде множителей. Причем результатом сокращения является такая дробь, числитель и знаменатель которых уже невозможно сократить.

Правила сокращения обыкновенных дробей
Для начала стоит проверить, делится ли числитель на знаменатель или наоборот. Тогда именно на это число нужно провести сокращение. Это самый простой вариант.
Вторым является анализ внешнего вида чисел. Если оба заканчиваются на один или несколько нолей, то их можно сократить на 10, 100 или тысячу. Здесь же можно заметить, являются ли числа четными. Если да, то смело можно сокращать на два.
Третьим правилом того, как сократить дробь, становится разложение на простые множители числителя и знаменателя. В это время нужно активно использовать все знания о признаках делимости чисел. После такого разложения остается только найти все повторяющиеся, перемножить их и произвести сокращение на получившееся число.
Как быть, если в дроби стоит алгебраическое выражение?
Здесь появляются первые трудности. Потому что именно здесь появляются слагаемые, которые могут быть идентичны множителям. Их очень хочется сократить, а нельзя. До того как сократить алгебраическую дробь, ее нужно преобразовать так, чтобы она имела множители.
Для этого потребуется выполнить несколько действий. Возможно, потребуется пройти их все, а может, уже первое даст подходящий вариант.
Проверить, не отличаются ли числитель и знаменатель или какое-либо выражение в них на знак. В этом случае необходимо просто вынести за скобки минус единицу. Так получаются одинаковые множители, которые можно сократить.
Посмотреть, можно ли вынести из многочлена за скобки общий множитель. Возможно, так получится скобка, которую также можно сократить, или это будет вынесенный одночлен.
Попробовать провести группировку одночленов с тем, чтобы потом в них вынести общий множитель. После этого может оказаться, что появятся множители, которые можно сократить, или снова повторить вынесение за скобки общих элементов.
Попытаться рассмотреть в записи формулы сокращенного умножения. С их помощью легко удастся преобразовать многочлен в множители.
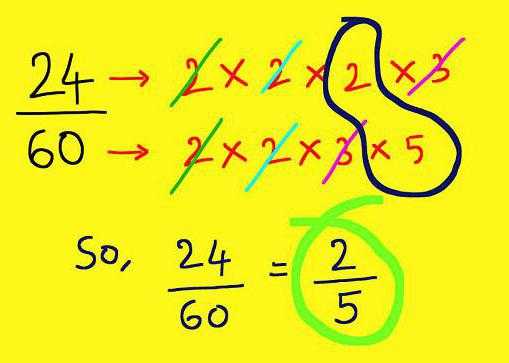
Последовательность действий с дробями со степенями
Для того чтобы без проблем разобраться в вопросе о том, как сократить дробь со степенями, необходимо твердо запомнить основные действия с ними. Первое из них связано с умножением степеней. В этом случае, если основания одинаковые, показатели необходимо сложить.
Второе — деление. Опять же у тех, которые имеют одинаковые основания, показатели потребуется вычесть. Причем вычитать нужно из того числа, которое стоит в делимом, а не наоборот.
Третье — возведение в степень степени. В этой ситуации показатели перемножаются.
Для успешного сокращения потребуется также умение приводить степени к одинаковым основаниям. То есть видеть, что четыре — это два в квадрате. Или 27 — куб трех. Потому что сократить 9 в квадрате и 3 в кубе сложно. Но если преобразовать первое выражение как (32)2, то сокращение пройдет успешно.
www.syl.ru