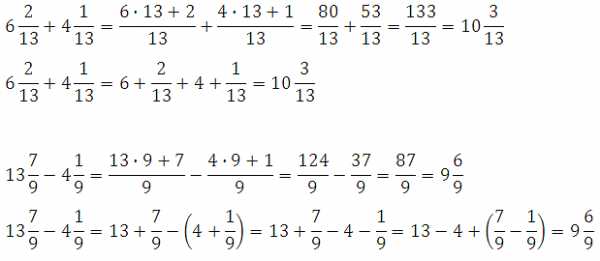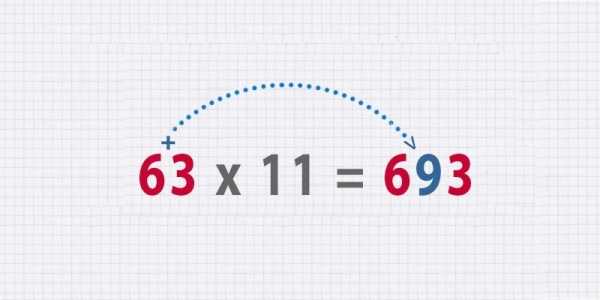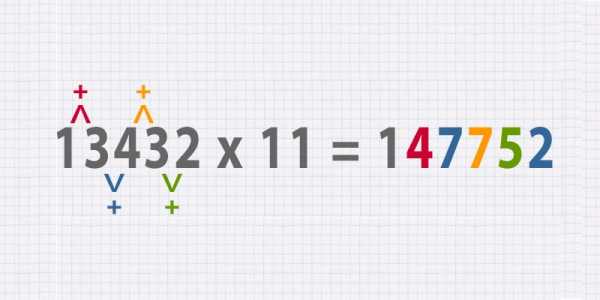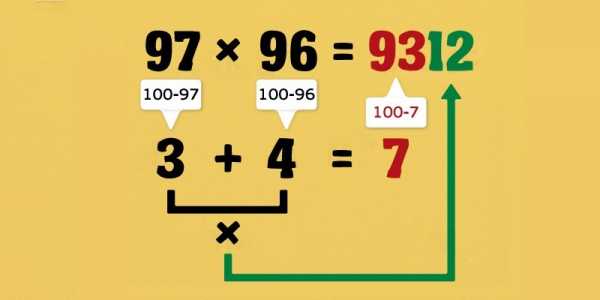Как складывать дроби с разными знаменателями. Как научить ребенка решать дроби 6 класс

Действия с дробями, подробно с примерами

Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь список материалов и изучать последовательно.

1. Сумма дробей, разность дробей.

Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.

Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь  – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.

Формальная запись суммы и разности дробей с равными знаменателями:

Примеры (1):

Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…

Вариант 1 – можно перевести их в обыкновенные и далее вычислять.

Вариант 2 – можно отдельно «работать» с целой и дробной частью.

Примеры (2):

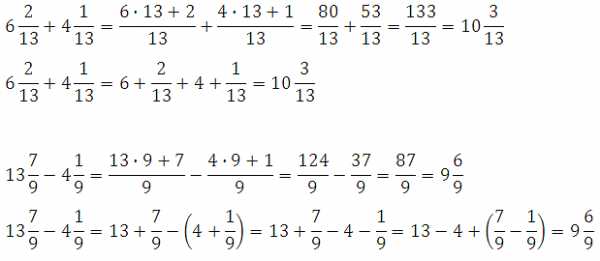
Ещё:

А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.

Примеры (3):

*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.

*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.

Ещё пример:

Вывод: имеется универсальный подход  – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие. После этого если в результате получаем неправильную дробь переводим её в смешанную.

Выше мы рассмотрели примеры с дробями, у которых равные знаменатели.  А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.

Рассмотрим простые примеры:

В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.

Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ.

То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразования.

Посмотрите на эти примеры:

К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.

Способ ВТОРОЙ.

Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

Пример:

*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.

Рассмотрим пример:

Видим, что числитель и знаменатель делится на 5:

Способ ТРЕТИЙ.

Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?

Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но  пары чисел могут быть и другими, например 51 и 119.

Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:

— разложить каждое из чисел на ПРОСТЫЕ множители

— выписать разложение БОЛЬШЕГО из них

— умножить его на НЕДОСТАЮЩИЕ множители других чисел

Рассмотрим примеры: 

50 и 60   =>  50 = 2∙5∙5    60 = 2∙2∙3∙5

в разложении большего числа не хватает одной пятёрки

 =>   НОК(50,60) = 2∙2∙3∙5∙5 = 300

48 и 72   =>   48 = 2∙2∙2∙2∙3    72 = 2∙2∙2∙3∙3            

в разложении большего числа не хватает двойки и тройки

=>   НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Наименьшее общее кратное двух простых чисел равно их произведению

Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.

Рассмотрим примеры:

*51 = 3∙17    119 = 7∙17

в разложении большего числа не хватает тройки

 =>   НОК(51,119) = 3∙7∙17

А теперь применим первый способ:

*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.

Ещё примеры:

*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.

ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!

— приводим дроби к обыкновенным, если есть целая часть.

— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).

— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).

— если необходимо, то результат сокращаем.

— если необходимо, то выделяем целую часть.

2. Произведение дробей.

Правило простое. При умножении дробей умножаются их числители и знаменатели:

Примеры:

Если есть возможность сократить дробь на стадии вычисления, то лучше это сделать:

Ещё правило относящееся к умножению!

Примеры, которые мы уже рассмотрели:

Определить, сколько составляет 3/7 от числа 63?

Задача. Весь путь составляет 180 километров. Турист в первый день прошёл 3/10 пути. Сколько километров турист прошёл в первый день?

Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм  картофеля завезли на базу?

С произведением закончим.

*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:

3. Деление дробей.

Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:

Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:

Примеры:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Делитесь информацией в социальных сетях.

matematikalegko.ru

Простые дроби, дробь, знаменатель дроби, числитель дроби | Формулы и расчеты онлайн

Простой дробью (или просто, дробью) называется часть единицы или несколько равных частей (долей) единицы.

простые дроби, числитель, знаменатель. Кольцо разделено на 5 секторов. 3 из них красные.

Числитель дроби — Число, показывающее количество взятых долей.

Запись:

\[ \frac{3}{5} \]

или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель.

Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:

\[ \frac{3}{5} - правильная дробь. \]

Если числитель равен знаменателю, дробь равна единице.

Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной.

Например:

\[ \frac{5}{5} , \frac{17}{5} - неправильные дроби. \]

Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному.

Например:

\[ \frac{45}{5} = 45 : 5 = 9 \]

Смешанные числа

Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.

Пример:

Дана дробь

\[ \frac{48}{5} \]

Делим 48 на 5. Получаем частное 9 и остаток 3.

\[ \frac{48}{5} = 9 \frac{3}{5} \]

Число, содержащее целую и дробную части

\[ 9 \frac{3}{5} \]

называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью.

Например:

\[ 7 \frac{13}{5} \]

тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).

Например:

\[ 7 \frac{13}{5} = 7 + \frac{13}{5} = 7 + 2\frac{3}{5} = 9\frac{3}{5} \]

К подобному виду обычно и приводят смешанные числа.

Часто приходится (например, при умножении дробей) решать вопрос обратного характера:

Дается смешанное число,требуется представить его в виде дроби (неправильной).Для этого нужно:1) целое число, входящее в смешанное, помножить на знаменатель дробной части;2) к произведению прибавить числитель.Полученное число будет числителем искомой дроби, знаменатель остается прежний.

Пример:

Дано смешанное число

\[ 9 \frac{3}{5} \]

\[ 9 · 5 = 45\]

\[ 45 + 3 = 48\]

\[ 9 \frac{3}{5} = \frac{48}{5} \]

В помощь студенту

Простые дроби, дробь, знаменатель дроби, числитель дроби

www.fxyz.ru

Как научить ребенка математике

Для многих математика как темный лес, и кажется, что разобраться во всём этом просто невозможно. Но что, если посмотреть на это под другим углом? К примеру, воспринимать математику не как что-то сложное и скучное, а как любопытную головоломку. Для этого мы предлагаем 10 математических трюков, которые перевернут твое представление о математике. Этого нет ни в одном учебнике!

Как научить ребенка математике

10 хитрых трюков

1. Умножение чисел, состоящих из единиц, на самих себяВозьми эту таблицу на вооружение, с ней решать такие примеры станет проще простого.
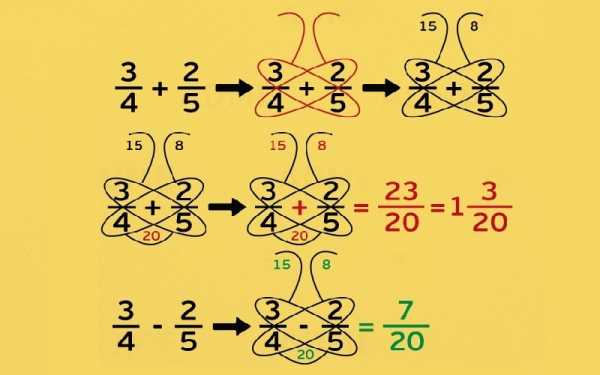
2. Метод бабочки для сложения и вычитания дробей Разобраться в этой схеме очень легко. В выбранном примере умножаем числа по диагонали. Если дроби нужно сложить, получившиеся числа также нужно сложить, аналогично при вычитании. Это будет наш числитель. После умножаем числа в знаменателе — получаем ответ!
3. Секрет умножения чисел на 11Представьте следующий пример: 63 × 11.Для его решения нужно просто сложить цифры 6 + 3 = 9, а затем поместить девятку между шестеркой и тройкой. Вот и наше решение: 693.

   Но расслабляться еще рано: это лишь половина того, что необходимо знать.

   Допустим, пример такой: 85 × 11.Несмотря на то, что 8 + 5 = 13, ответ не 8135! Как и прежде, цифра 3 ставится между цифрами 8 и 5, но 1 добавляется к цифре 8 для получения правильного ответа 935.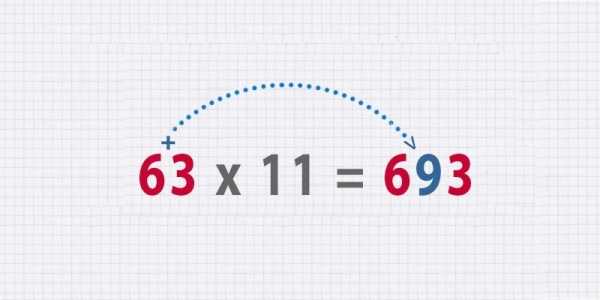

4. Можно ли использовать этот метод для чисел с большим количеством цифр? Безусловно!Здесь уже немного сложнее, но не стоит огорчаться, у тебя всё получится. Для примера: 13432 × 11 — ответ всё еще будет начинаться с 1 и заканчиваться на 2, а так как 1 + 3 = 4; 3 + 4 = 7; 3 + 4 = 7 и 3 + 2 = 5, ответ будет равен 147752.
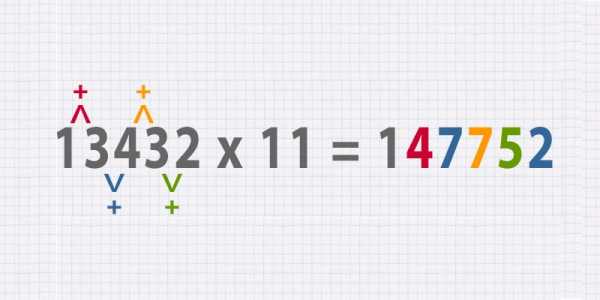
5. Находим дробь от целого числа Пользуйся этой схемой и забудь о проблемах с дробями! Это и есть ответ на вопрос, как научить ребенка решать математические примеры.
6. Умножать на 9 проще, чем ты думаешь!Эта забавная закономерность поможет тебе без труда запомнить таблицу умножения на 9 навсегда.
7. Преврати сложное умножение в простые примерыЭтот трюк уже немного похож на магию. Всё, что нужно, — вычесть множители из 100, а произведения сложить и умножить. Сумма, вычтенная из 100, — это первая часть ответа, а произведение — вторая.
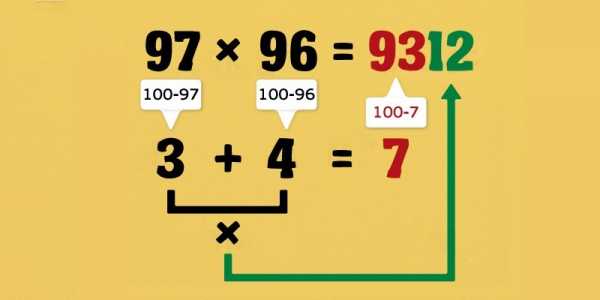
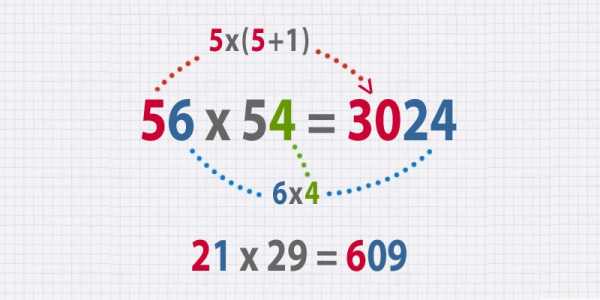
8. А это еще один способ умножать большие числа

   

9. Запомнить число Пи теперь не составит труда
   
10. Так можно с легкостью найти процент от числа

Теперь математика уже не кажется такой скучной, правда? Благодаря этим трюкам ты можешь объяснить ребенку математику и сделать решение примеров интересным и увлекательным занятием!

А также ты можешь поделиться этими трюками с друзьями. Уверены, это им пригодится!

Автор статьи

Редакция «Так Просто!»

Это настоящая творческая лаборатория! Команда истинных единомышленников, каждый из которых специалист в своем деле, объединенных общей целью: помогать людям. Мы создаем материалы, которыми действительно стоит делиться, а источником неиссякаемого вдохновения служат для нас любимые читатели!

takprosto.cc

Как научиться решать дроби

Дробь представляет собой число, состоящее из одной или нескольких равных долей единицы. С дробями можно выполнять те же арифметические действия, что и с целыми числами: сложение, вычитание, умножение и деление.

Инструкция

1

2

3

4

5

masterotvetov.com

Как запомнить | Учитель математики.ру

Для того, чтобы помочь ученикам запомнить математические понятия и поддержать интерес к предмету, полезно использовать некоторые приёмы и методы.

Тема "Обыкновенная дробь"

Например, при изучении темы "Обыкновенная дробь" можно выучить прямо на уроке со своими детьми такое стихотворение:

Каждый может за версту Видеть дробную черту. Над чертой - числитель, знайте Под чертою - знаменатель. Дробь такую, непременно, Надо звать обыкновенной.

Чтобы ученики с самого начала изучения темы не путали расположение числителя и знаменателя дроби, воспользуйтесь таким предложением "Человек стоит на земле" и соответствующим рисунком.

Слово "человек" начинается на букву "ч" и слово "числитель" тоже начинается на букву "ч".

Слово "земля" начинается на букву "з" и слово "знаменатель" тоже начинается на букву "з".

Значит, числитель и знаменатель дроби будут расположены по отношению друг к другу точно так, как человек и земля, изображённые на рисунке.

Человек сверху, земля снизу и, соответственно, числитель сверху, знаменатель снизу.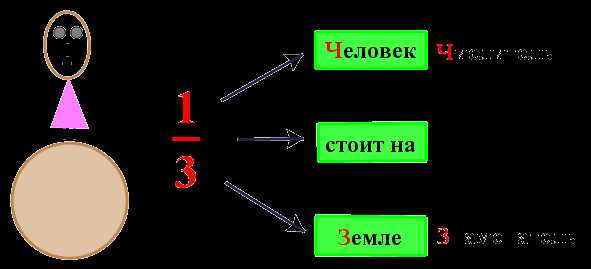

Как запомнить значение числа "π"

Первым классическим примером иррационального числа, с которым знакомятся учащиеся, является число π.

Значение числа π представляет собой бесконечную непериодическую десятичную дробь. Для работы вполне достаточно знать приближённое значение этого числа, равное .

Но для разнообразия можно познакомить учеников со стихотворением, которое позволит запомнить десятичных знаков этого числа.

Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.

В результате получаем приближённое значение числа π, равное .

 Как запомнить значение числа "e"

При изучении логарифмов учащиеся знакомятся со вторым классическим примером иррациональных чисел. Это число , основание натурального логарифма.

Значение числа  также представляет собой бесконечную непериодическую десятичную дробь. Как правило, учителя предлагают запомнить только один десятичный знак .

И как бывает интересно, когда учитель говорит: "А я знаю девять десятичных знаков числа !" После этого записывает на доске .

Мнемоническое правило, которое позволяет запомнить девять цифр после запятой, очень простое.

Оказывается, число  это и дважды Лев Толстой. Фраза "дважды Лев Толстой" означает, что нужно два раза записать год рождения Льва Николаевича Толстого.

Число представляет собой год рождения великого писателя. В итоге получаем .

Практического значения знание девяти цифр после запятой у числа для ученика средней школы не имеет, но знакомство с этим фактом украсить урок и вызвать неподдельный интерес практически у каждого ученика. Кроме того, это и пример замечательной межпредметной связи.

vebuchitel.ru

Как складывать дроби с разными знаменателями

Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.

Чтобы сложить или вычесть дроби с разными знаменателями, надо:

1) Найти наименьший общий знаменатель (НОЗ) данных дробей.

2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.

3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.

4) Проверить, является ли полученная в результате дробь правильной и несократимой.

В следующих примерах надо сложить или вычесть дроби с разными знаменателями:

Решение:

1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей. Выбираем большее из чисел и проверяем, делится ли оно на меньшее. 25 на 20 не делится. Умножаем 25 на 2. 50 на 20 не делится. Умножаем 25 на 3. 75 на 20 не делится. Умножаем 25 на 4. 100 на 20 делится. Значит, наименьший общий знаменатель равен 100.

2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.

3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.

4) Полученная дробь — правильная и несократимая. Значит, это — ответ.

1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.

2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.

3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.

4)Полученная в результате дробь — правильная и несократимая.

1) 30 на 20 не делится. 30∙2=60 на 20 делится. Значит, 60 — наименьший общий знаменатель этих дробей.

2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.

3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.

4) полученную дробь надо сократить на 5.

1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.

2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.

3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.

www.for6cl.uznateshe.ru

• 
  Как давать ребенку 6 месяцев мясное пюре
• 
  Ребенку 1 год 6 месяцев не разговаривает
• 
  Сколько весил ваш ребенок в 6 месяцев
• 
  Во что поиграть с 6 летним ребенком
• 
  Как помочь ребенку в учебе 6 класс
• 
  Овощной суп для ребенка для 6 месяцев
• 
  Упражнения на фитболе для ребенка 6 месяцев
• 
  Ребенок 6 месяцев не какает 3 дня
• 
  Ребенку 6 месяцев гноится глаз что делать
• 
  Сколько ваш ребенок весил в 6 месяцев
• 
  Как развести смекту для ребенка 6 лет