Какие геометрические фигуры должен знать ребенок в 4 года:  РАЗВИТИЕ РЕБЕНКА: Геометрические фигуры. Развиваем память.

Изучаем геометрические фигуры: игры для детей дошкольного возраста

Одним из важных аспектов развития математических представлений у дошкольников является изучение основ геометрии. В ходе знакомства с геометрическими фигурами, ребенок приобретает новые знания о свойствах предметов (форме) и развивает логическое мышление. В этой статье мы поговорим о том, как помочь дошкольнику запомнить геометрические фигуры, как правильно организовать игры для обучения геометрии, а также о том, какие материалы и пособия можно использовать для развития математических способностей малыша.

В каком возрасте можно начинать изучать геометрические фигуры?

Многих родителей посещает вопрос, нужно ли маленьким детям знакомиться с геометрическими фигурами. Специалисты считают, что занятия в игровой непринужденной форме оптимально начинать с 1,5 лет. До этого возраста уместно проговаривать ребенку названия форм предметов, с которыми малыш встречается в реальной жизни (например, «тарелка круглая», «стол квадратный»).

Знакомя ребенка с геометрическими фигурами, ориентируйтесь на его реакцию. Если малыш начал проявлять к ним интерес в раннем возрасте (играя с сортером или рассматривая картинки), поощряйте его любопытство.

В 2 года малыш должен уметь различать:

• Круг;
• Квадрат;
• Треугольник.

К 3 года к ним можно добавить:

• Овал;
• Ромб;
• Прямоугольник.

В более старшем возрасте ребенок может запомнить такие фигуры, как трапеция, пятиугольник, шестиугольник, звезда, полукруг. Также дети, посещающие Монтессори-центр «Созвездие», с интересом знакомятся с геометрическими телами.

Как помочь ребенку запомнить геометрические фигуры?

Обучение ребенка геометрическим формам должно происходить поэтапно. Приступать к новым фигурам нужно только после того, как малыш запомнит предыдущие. Самой простой фигурой считается круг. Покажите ребенку круглые предметы, пощупайте их, пусть малыш проведет по ним пальчиком. Также можно сделать аппликацию из кругов, слепить круг из пластилина. Чем больше ощущений, связанных с изучаемым понятием, получит ребенок, тем лучше малыш его запомнит.

Для знакомства с формами можно использовать объемные фигуры. Это могут быть делали конструктора, сортера, шнуровки, рамок-вкладышей. Так как в раннем возрасте наиболее развит наглядно-действенный тип мышления, то различные действия с фигурами помогут лучше их запомнить.

Как дети разного возраста воспринимают геометрические фигуры

Операции, которые ребенок может производить с геометрическими фигурами, и то, как он воспринимает формы, зависят от возраста малыша. В соответствии с возрастными особенностями, можно выделить следующие этапы обучения:

1. На втором году жизни малыш способен зрительно распознавать знакомые ему фигуры и сортировать предметы по форме.
2. В 2 года ребенок может найти нужную фигуру среди ряда других геометрических фигур.
3. К 3 годам малыши могут называть фигуры.
4. В 4 года ребенок способен соотносить объемную фигуры с плоским изображением.
5. В старшем дошкольном возрасте (а иногда и раньше) можно начинать изучение геометрических тел (шар, куб, пирамида). Также в этом возрасте ребенок может анализировать сложные картинки, состоящие из множества фигур.

В независимости от возраста малыша старайтесь обращать его внимание на формы окружающих предметов и сопоставлять их с известными геометрическими фигурами. Это можно делать дома и на прогулке.

Игры для изучения геометрических фигур

Чтобы ребенку было интересно, обучение геометрическим фигурам должно происходить в игровой форме. Следует также подбирать яркие и красочные материалы для занятий (их можно приобрести в магазине или сделать своими руками). Вот некоторые примеры игр и пособий для изучения геометрических фигур:

1. Сортировка. Игры с сортером можно начинать уже с 1 года. Предложите малышу найти для фигуры ее окошко. Так ребенок будет не только запоминать геометрические фигуры, то и развивать мелкую моторику, мышление и пространственные представления, ведь чтобы деталь попала в отверстие, нужно повернуть ее под правильным углом. Сортировать можно и любые другие предметы, например, элементы конструктора, блоки Дьенеша или счетный материал.
2. Рамки вкладыши. По сути, это пособие аналогично сортеру. Для каждой геометрической фигуры необходимо найти ее место.
3. Геометрическое лото. Для игры понадобится поле с изображением геометрических фигур и раздаточные карточки с каждой фигурой в отдельности. Маленькие карточки ребенок может доставать из сундучка или мешочка, а затем искать их место на игровом поле. Эта игра также отлично тренирует внимание малыша.
4. Геометрическая аппликация. Вырежьте из бумаги различные геометрические фигуры и вместе с ребенком составьте из них картинку (например, из треугольников можно сделать елочку, из квадрата и треугольника – домик).

5. Рисование (в том числе, при помощи трафаретов).
6. Лепка.
7. Выкладывание фигур из счетных палочек.
8. Геометрическая мозаика.
9. Шнуровки с геометрическими фигурами.
10. Игры с карточками.
11. «Угадай на ощупь».
12. Активные игры. На асфальте мелом нарисуйте геометрические фигуры. Попросите малыша представить, что фигуры – это домики, в которые надо забежать по сигналу. Далее Вы называете геометрическую фигуру, а ребенок бежит к ней.

Кроме того, для изучения геометрических фигур можно использовать развивающие мультфильмы. Вот один из них:

Выводы

Обучение основам геометрии в дошкольном возрасте является важной частью формирования у ребенка математических и сенсорных представлений. Знакомство с фигурами должно происходить постепенно (сначала простые фигуры – круг, квадрат, треугольник). Чтобы малышу было интересно, занимайтесь изучением геометрических фигур в игровой форме. Вашими помощниками в этом могут стать такие развивающие пособия, как рамки-вкладыши, мозаики, лото, сортеры, наборы геометрических фигур и тел, трафареты. Изучать геометрические фигуры можно и на улице: просто проговаривайте с ребенком, что вы видите вокруг и на какие фигуры похожи эти предметы. Тогда малыш обязательно научится различать геометрические фигуры и запомнит их названия.

Заключение

Для всестороннего и гармоничного развития каждого малыша в детском центре «Созвездие» специально создана Монтессори-среда. В процессе свободной работы в ней дети не только знакомятся с основами геометрии, но и развивают свои познавательные процессы, мелкую моторику, учатся писать, читать, считать. Кроме этого Монтессори-среда дает ребенку возможность в полной мере проявить самостоятельность и ответственность. Будем рады видеть Вас и Вашего малыша у нас в центре!

Статью подготовила Монтессори-педагог

Малышева Евгения

Старшая группа (5-6 лет)

   Данная статья предназначена для вашего ознакомления и дает примерные нормы степени сформированности психических процессов вашего ребенка в этом возрасте. Вы можете проверить его потенциальные возможности в разных областях знаний, узнать, в каких областях знаний Ваш ребенок преуспевает, а в каких требуется дополнительное внимание и время.

Математика

1. Ребенок может уметь решать простейшие задачки и головоломки.

2. Ребенок  может уметь вычитать и прибавлять к числу.

3. Ребенок   может уметь определять направление: вперед, назад, направо, налево, вверх, вниз.

4. Ребенок  может уметь считать предметы в пределах 10 на основе действий со множествами.

5. Ребенок   может уметь сравнивать числа: равенства- неравенства, больше — меньше.

6. Ребенок   может понимать и правильно отвечать на вопросы: Сколько? Который? Какой по счету?

7. Ребенок   может знать состав чисел первого десятка.

8. Ребенок  может уметь различать и называть предметы круглой, квадратной, треугольной и прямоугольной формы.

9. Ребенок  может знать такие геометрические фигуры как: квадрат, прямоугольник, круг, треугольник, трапеция, ромб; геометрические тела: куб, шар, цилиндр, пирамида.

10. Ребенок   может знать знаки «+», «-«, «=», «<;» и «>;».

11. Ребенок  может уметь составлять и решать задачи в одно действие на сложение и вычитание.

12. Ребенок  может  уметь разделить круг, квадрат на две и четыре равные части.

13. Ребенок  может  знать прямой и обратный порядок числового ряда.

Логическое мышление
Развитие Мышления, Памяти, Внимания

1.Ребенок   может отвечать на такие вопросы как:

2.Ребенок   может уметь выполнять задания в которых необходимо выявить закономерность и продолжить ряд из предложенных предметов.

3. Ребенок  может  находить лишний предмет из 4-5 предложенных предметов.

4. Ребенок  может  уметь составлять рассказ по предложенным картинкам, уметь заканчивать рассказ (придумать конец).

5. Ребенок  может  уметь разделять предложенные предметы на две группы и находить для каждой группы общий признак.

Развитие речи

1.Ребенок  может  называть свое имя, фамилию, сколько ему лет, называть город в котором живет, как зовут родителей, сколько им лет, где и кем они работают.

2. Ребенок  может  знать домашний адрес, номер домашнего телефона

3. Речь у ребенка  может  быть максимально приближена к взрослой речи (по качеству).

4. Ребенок   может знать, что такое интонация, должен пользоваться ею для выражения своих эмоций.

5. Ребенок   может  уметь отличать побудительное предложение от повествовательного, восклицательное от вопросительного, должен уметь их использовать.

6. Ребенок   может уметь формулировать и задавать вопросы, строить рассуждения, спорить.

7. Ребенок   может уметь вести диалог и монолог.

8. Ребенок   может знать много наизусть выученных стихотворений, сложных и больших по объему произведений. Рассказывать он должен с выражением.

Окружающий мир

1.Ребенок  может  знать названия всех окружающих его предметов: мебель, посуда, одежда, бытовые и электроприборы, растений, животных, явлений природы, названия любимых мультфильмов, сказок, книжек, имена любимых героев.

Навыки обихода

1. Ребенок   может уметь звонить по телефону.

2.Ребенок   может знать как вдеть нитку в иголку, как пришить пуговицу

3. Ребенок  может уметь вести себя за столом.

4. Ребенок  может самостоятельно чистить зубы, полоскать рот после приема пищи.

5. Ребенок может  уметь застегивать пуговицы, завязывать шнурки.

6. Ребенок  может  знать, что значит быть опрятным, должен уметь следить за прической, за ногтями и состоянием одежды.

7. Ребенок может  знать для чего нужен светофор, для чего нужен каждый цвет светофора, как и где можно переходить дорогу.

8. Ребенок  может  знать название текущего месяца, последовательность дней недели.

Когда дети изучают фигуры?

7 февраля 2020 г. Тони

Раскрытие информации: Этот пост может содержать партнерские ссылки, то есть я получаю комиссию, если вы решите совершить покупку по моим ссылкам бесплатно для вас. Как партнер Amazon, я зарабатываю на соответствующих покупках. Полное раскрытие читайте здесь.

Когда дети изучают формы? Каждый новый родитель ребенка беспокоится о развитии своего ребенка, но каждый ребенок развивается немного по-разному. Да, есть несколько ключевых маркеров, которые дети, как известно, достигают в определенный период времени, но не стоит беспокоиться, если они не достигают цели вовремя. Ярким примером этого является ребенок, изучающий различные формы.

Когда ребенок должен знать свои формы?

Двухлетний возраст — прекрасное время для начала занятий с ребенком по изучению форм, но важно начинать с основных форм. Основы включают квадрат, прямоугольник, круг и треугольник, и дети обычно понимают и узнают их в возрасте 2 1/2 лет. Их можно усилить, указывая на предметы одинаковой формы.

Когда они поймут основы, пора переходить к более сложным формам, включая овал, сердце, звезду и ромб. К 3 годам они должны хорошо понимать их все, но не расстраивайтесь, если они все еще немного борются. Это может быть немного сложнее найти объекты одинаковой формы, но это не невозможно.

Краткое изложение того, когда дети изучают фигуры:

• Начинают обучать фигурам в 2 года
• Понимают и распознают основные формы в возрасте 2-1/2 лет
• В возрасте 3 лет они смогут определять диапазон фигур

Какие фигуры должен знать трехлетний ребенок?

Как указывалось ранее, 3-летний ребенок должен хорошо понимать и уметь распознавать самые основы: квадрат, прямоугольник, круг и треугольник, но он также должен понимать овалы, сердца, звезды, и бриллианты. Некоторые другие, которым следует учить ребенка в возрасте до трех лет, — это пятиугольник, шестиугольник и восьмиугольник.

Как дети изучают формы?

Есть много замечательных вещей, которые могут помочь детям выучить формы. Одна из таких вещей включает в себя классическую игрушку, в которой дети помещают трехмерные фигуры в соответствующие отверстия. Многие люди покупают эту игрушку для своих детей, потому что она помогает развивать их моторные навыки, заставляя их перемещать их и вставлять в отверстия правильной формы.

Родитель также может использовать эту игрушку, чтобы постепенно обучать детей, показывая, какую фигуру они держат в руке, и предлагая найти отверстие в этой фигуре. Ниже приведены две игрушки, которые часто рекомендуются, потому что они очень помогают в изучении форм, но они также могут помочь в изучении цветов.

Educational Insights Shapes Beanbags

Продажа

Educational Insights Shapes Beanbags, Learn Shapes, обучающая игрушка для малышей, обязательные предметы для дошкольного класса, набор из 8 Beanbags, возраст 3+

• ИСКРИ БОЛЬШЕ УВЕРЕННОСТИ! Дошкольники играют по-своему, формируя личность, развивая уверенность в себе и ключевые навыки раннего обучения
• ПОЛНОСТЬЮ ТАКТИЛЬНАЯ ОБУЧАЮЩАЯ ДЕЯТЕЛЬНОСТЬ! Сделайте развитие навыков более увлекательным с помощью этого практического занятия «бросай и лови» для раннего обучения

Последнее обновление от 18. 12.2022 / Партнерские ссылки / Изображения из Amazon Product Advertising API

Эта игрушка безопасна для детей в возрасте от 36 месяцев. Этот продукт состоит из 8 погремушек разной формы, на которых напечатано их название. Формы, в которые изготавливаются эти погремушки: круг, треугольник, квадрат, прямоугольник, пятиугольник, овал, звезда и шестиугольник.

Каждая из сумок разного цвета, поэтому их также можно использовать для изучения цветов. Эти цвета являются основными оттенками каждого цвета: красный, фиолетовый, зеленый, розовый, желтый, синий, оранжевый и коричневый. Они поставляются с сумкой на шнурке для хранения мешков с фасолью, когда они не используются, и их легко взять с собой, чтобы навестить бабушку и дедушку.

Благодаря тому, что они представляют собой мешочки с фасолью, двигательные навыки ребенка могут быть лучше развиты, потому что родители могут заставить ребенка подбрасывать их в правильную форму. Самое замечательное в этих креслах-мешках, которые нравятся родителям, заключается в том, что их можно полностью стирать, так как они сделаны из войлока, что также делает их легкими и безопасными для ребенка.

Размер каждого кресла-мешка составляет от 4 до 5 дюймов, что делает его идеальным для маленького ребенка. Они поставляются с удобным листом, называемым подсказкой, который дает родителям уникальные и забавные действия, которые они могут делать с фигурами, чтобы сделать процесс обучения увлекательным.

Учебные материалы Пластиковые шаблоны блоков

Продажа

Учебные ресурсы Набор из 250 пластиковых шаблонов, игры с формами для дошкольников от 3 лет, товары для домашнего обучения, обучающие игры для дошкольников, манипуляции с формами для детей

Последнее обновление от 18 декабря 2022 г. / Партнерские ссылки / Изображения из Amazon Product Advertising API

Эта игрушка отлично подходит для использования на плоской и твердой поверхности, например на столе. Они очень маленькие, поэтому дети, которые все же склонны засовывать в рот предметы, не должны иметь к ним доступа без строгого присмотра. Всего 250 штук, и они поставляются в небольшой пластиковой ванне, что означает, что их можно легко убрать.

В ванне можно найти 6 различных форм, каждая из которых имеет свой цвет. Включены формы шестиугольника, квадрата, трапеции, треугольника, ромба и параллелограмма, а цвета включают красный, зеленый, желтый, синий, коричневый и оранжевый.

Одна вещь, которая делает эти обучающие игрушки более уникальными, чем другие, заключается в том, что дети могут складывать их вместе, образуя другие фигуры или создавая большой узор. Прямые стороны этих игрушек можно использовать, чтобы научить ребенка измерять линейкой.

Родителям следует помнить, что контейнер сделан из тонкого пластика, и если его слишком много раз помять, он станет слабее. Это означает, что было бы разумно заглянуть в какой-нибудь контейнер, чтобы в конечном итоге их поместить. Из-за их размера рекомендуемый возраст составляет 4 года.

Заключение

Если у вас возник вопрос: «Когда дети изучают фигуры?» Теперь у вас есть лучшее понимание. Если вы только начинаете, пришло время поработать с малышом над основными фигурами. Вы также можете узнать, когда дети учат цвета.

Что дети знают и должны знать о форме и пространстве

Геометрия включает в себя два основных компонента. Один рассуждает о форме . Мы узнаем, например, что треугольники должны иметь три прямые стороны и три угла, но углы могут быть узкими или широкими, а треугольники могут быть высокими или короткими, красными или синими или наклоненными любым количеством способов. Второй компонент думает о пробел . Мы узнаем, как объекты относятся друг к другу и к нам в пространстве: мяч на диване, диван под мячом, а мы перед ними обоими.

Несмотря на то, что дети точно воспринимают форму и пространство в повседневной жизни, дошкольники в возрасте от трех до пяти лет должны научиться думать на эти темы. Наша главная образовательная цель должна заключаться в содействии пониманию основ геометрии.

Форма

Контекст и обзор

Восприятие объектов начинается вскоре после рождения. С самых ранних дней и примерно до 18 месяцев младенцы могут легко видеть различия между обычными объектами: они видят, что мать отличается от отца, а собака отличается от кошки. Младенцы могут различать типы объектов: они видят, что это тарелка, а это чашка, даже если они не знают названия каждого из них и не могут сформулировать ключевые различия между ними. Далее, младенцы могут опознавать предметы даже тогда, когда они меняют свое местонахождение: это мать независимо от того, видим ли мы ее с той или иной стороны, близко она или далеко, лежит или стоит, частично или полностью видна.

К концу младенчества восприятие объектов развито относительно хорошо, и дети относительно легко ориентируются в повседневном мире. В то же время им предстоит еще многому научиться, в частности, анализу форм, т. е. пониманию их существенных признаков. Выучить названия форм легко. Но анализировать их намного сложнее. Следовательно, основное внимание в обучении геометрии в раннем возрасте должно быть сосредоточено на анализе и понимании.

Ранние представления и представления о форме

В возрасте примерно трех-четырех лет дети изучают несколько аспектов форм, как двухмерных ( 2-D ), так и объемных ( 3-D ). Следующие иллюстрации в основном относятся к двумерным фигурам, но то же самое можно сказать и о твердых телах.

Восприятие различия и сходства   

Маленькие дети могут легко различать (видеть или воспринимать различия) между различными формами. Например, на вопрос, отличаются ли двумерные фигуры на рис. 1, дети быстро соглашаются, что да.

Они также могут легко различать трехмерные формы, например, между прямоугольной призмой (например, книгой) и сферой (например, шаром) или между сферой и кубом (например, блоком с шестью квадратными гранями). .

Совершенно очевидно, что маленькие дети могут видеть различия между треугольниками и прямоугольниками, а также между книгами и мячами. Они могут даже знать названия , треугольник и , прямоугольник . Но в то же время они могут быть не в состоянии проанализировать основания для своей дискриминации. Они могут ничего не знать о свойствах треугольников и прямоугольников. Например, они могут не понимать, что треугольник должен иметь три стороны, что это замкнутая фигура или что обе фигуры являются многоугольниками.

Короче говоря, способность различать означает только то, что дети видят что фигуры выглядят по-разному. В то же время дети могут не знать о себе ничего важного. Нам нужно различать видение и мышление, восприятие и мышление.

А как насчет идеи того же ? Маленькие дети могут видеть, что два прямоугольника воспринимаются одинаково или идентичны ( конгруэнтны ). Они могли бы даже увидеть конгруэнтность, если бы один из прямоугольников был немного наклонен в сторону (но не слишком сильно!). На рис. 2 показан пример.

Определить одинаковость в смысле конгруэнтной формы не очень сложно для маленьких детей, которые хорошо воспринимают, по крайней мере, то, что находится на поверхности. Их восприятие во многом невербальное и непосредственное. Обратите внимание, что язык не является существенным для любого из этих суждений: дети (или животные) могут видеть, что формы идентичны, но не могут назвать их. Дети также могут давать фигурам неправильные названия, но при этом точно воспринимать сходство (и различие). Например, вы можете сказать, что стая «собак» — это одно и то же, тогда как вам следовало бы назвать их «слонами». Объекты воспринимаются как одни и те же, как бы вы их ни называли.

Рисунок 3 иллюстрирует интересное усложнение. Иногда кажется, что дети не видят четкой разницы. Например, трехлетний ребенок может сказать, что фигуры на рис. 3 одинаковы, потому что обе они имеют «заостренные вершины».

Значит ли это, что ребенок не видит разницы между фигурами? Не обязательно. Ребенок, вероятно, видит различия, но думает , что формы тем не менее одинаковы. Если взрослый спросит, отличаются ли фигуры вообще, ребенок может сказать, что у одной три стороны, а у другой четыре, но они одинаковы, потому что у каждой есть «заостренная вершина». Итак, ребенок видит разницу в восприятии, но думает, что формы одинаковы, потому что каждая из них имеет общую вершину сверху. На самом деле ребенок совершенно прав: хотя формы различны, они одинаковы в свойстве, которое описывает ребенок. Это одна из причин опросить детей, чтобы попытаться раскрыть мышление, лежащее в основе их открытых ответов. Ребенок может сказать «одинаковые», но также понимать, что формы отличаются в другом отношении.

Классификация. Маленькие дети должны выйти за пределы восприятия сходства и различия. Они должны научиться классифицировать объекты, которые похожи (в отличие от конгруэнтных) в ключевых отношениях. Им нужно усвоить, что трехсторонние фигуры разного размера — это все треугольники; что неконгруэнтные, но подобные четырехсторонние фигуры с одинаковой длиной и прямыми углами являются квадратами; что баскетбольные мячи и глобусы — это сферы; и что блоки разного цвета могут быть кубиками.

Некоторые классификации проще для детей младшего возраста, чем другие. Например, они могут видеть, что квадраты разных размеров сочетаются друг с другом. Они могут идентифицировать прототипы, то есть стандартные общие треугольники, подобные показанным на рис. 4, независимо от их размера. Опять же, это можно сделать, не зная имен. Как бы цифры не назывались, одни идут вместе, а другие нет.

Имена. Конечно, детям нужно учить правильные имена. Имена полезны несколькими способами: они позволяют вам общаться с другими («Это треугольник»), а также отсылают вас к категории для анализа («Это называется треугольником, как и эти. Интересно, как они одинаковый.»). Английские названия форм немного странные, потому что многие из них происходят от греческого или латинского. Например, слово треугольник  происходит от греческого слова «три угла». Напротив, китайские имена фигур прозрачны. На китайском языке название прямоугольника переводится как «четырехсторонняя форма». Несмотря на это, геометрические названия не представляют сложности для детей. Дети дошкольного возраста знают тысячи имен, в том числе специальные имена, такие как бронтозавр, или эзотерические имена героев мультфильмов, игрушек или фигурок. Учитывая их способность усваивать язык, маленькие дети не должны испытывать особых трудностей при изучении таких имен, как 9.0103 прямоугольная призма или пятиугольник . Но взрослый всегда должен помнить, что имена хотя и необходимы, но поверхностны. Дети должны научиться понимать свойства фигур, а не только то, как их сортировать или называть.

Понимание . Понимание многогранно. Дети должны научиться анализировать формы, определять определяющие их свойства и говорить о них. Им нужно узнать, что делает треугольник треугольником и чем треугольник отличается от квадрата. Им нужно усвоить, что квадрат является подклассом прямоугольников.

Как упоминалось выше, дети могут легко научиться классифицировать прототипы форм. Они узнают, что равносторонний, равнобедренный и прямоугольный треугольники — все это треугольники. В то же время дети могут не знать, что длинный, тонкий, разносторонний треугольник, подобный показанному на рис. 5, также является законным членом семейства треугольников и что все треугольники любого цвета могут быть маленькими или большими, вершиной к вершине. на боку или лежа на горизонтальном основании. Размер, цвет и ориентация не имеют значения, когда цель состоит в том, чтобы идентифицировать фигуры одного типа.

Основная задача ребенка состоит в том, чтобы получить четкое представление об определяющих свойствах форм.  Дети должны понимать, что у треугольника есть определенные определяющие свойства, а у квадрата — другие, и что эти формы неизменны при изменении размера, ориентации и цвета. Они также должны уметь говорить о формах; объяснить, почему треугольник является треугольником, даже если он не является прототипом.

Ограниченное понимание детьми существенных и второстепенных свойств может частично быть связано с ограниченным набором форм, которые они видят.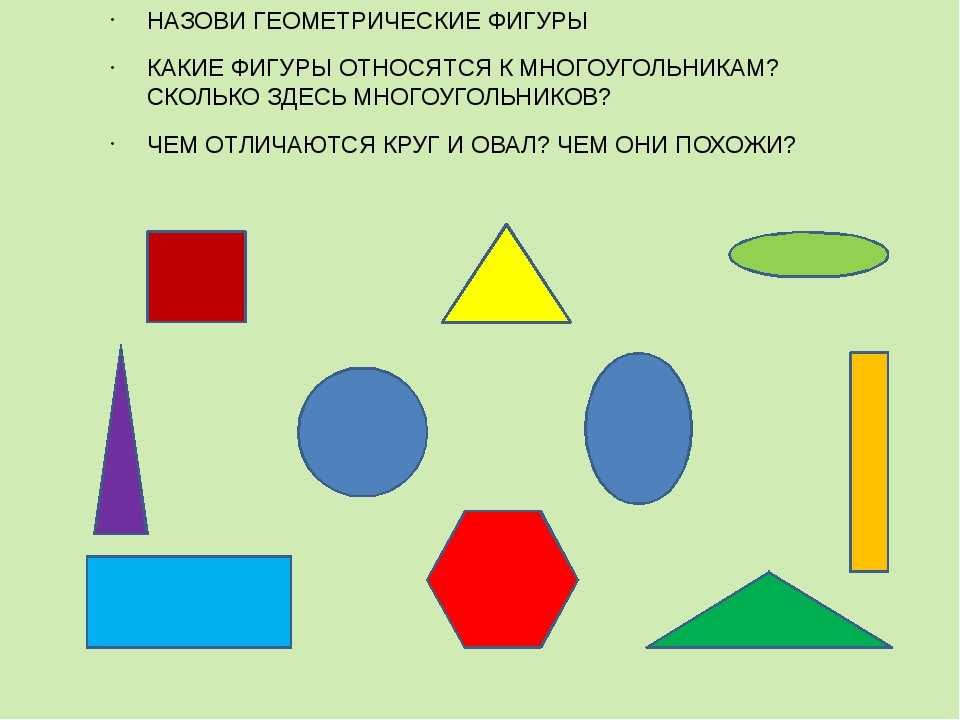 Дети часто сталкиваются с прототипами форм в книгах и игрушках. Если в книжке с картинками представлен треугольник, он, скорее всего, будет равносторонним или равнобедренным и редко разносторонним. Игрушки для сортировки по форме также включают в себя прототипы, в данном случае трехмерные, такие как равносторонняя треугольная призма.

Учитывая, что детям редко представляют непрототипные формы, взрослым необходимо знакомить детей с ними и учить их основным свойствам, разъясняя причины, по которым одна фигура является треугольником, а другая — пятиугольником. Как и в других областях, взрослые должны помочь детям 90–103 математизировать 90–104 их знания о формах, то есть развивать явное понимание формальной математики. Детям необходимо научиться думать и прямо говорить о математических свойствах, таких как количество вершин и сторон, определяющих фигуру.

Составление и разложение фигур . Детям также необходимо изучить и научиться разбирать фигуры и использовать фигуры для создания других фигур.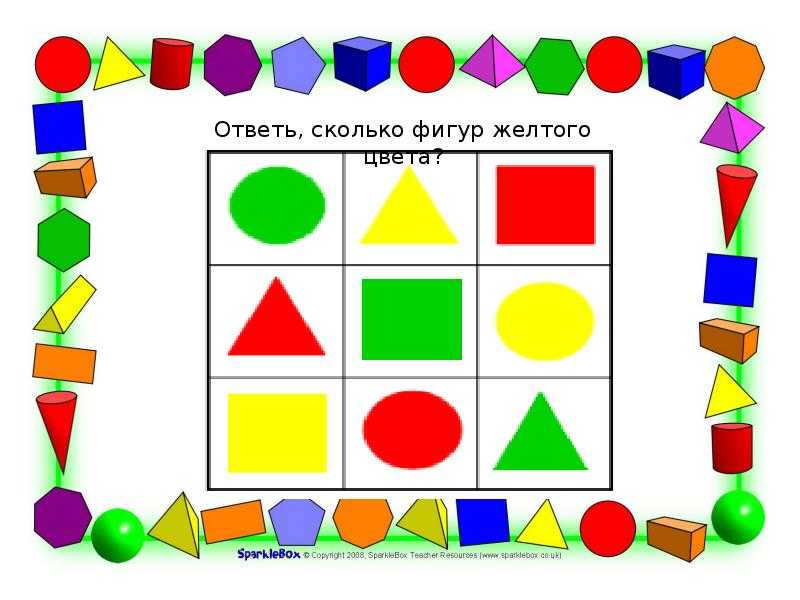 Например, если цель состоит в том, чтобы составить квадрат из двух треугольников, ребенок должен обратить внимание на внутренние углы и длины сторон треугольников. Композиция и декомпозиция способствуют анализу.

Дети могут исследовать формы, используя несколько заданий этого типа. Как показано на рисунке 6, дети могут составлять фигуры. Когда ребенок складывает вместе два квадрата одинакового размера, выравнивая их ширину, в результате получается длинный прямоугольник. Когда ребенок соединяет два одинаковых полукруга, выравнивая их диаметры, в результате получается полный круг.

Дети также могут разбирать фигуры. Как показано на рис. 7, когда ребенок делит прямоугольник по диагонали или разрезает равносторонний треугольник посередине, ребенок получает два прямоугольных треугольника.

Составление и разложение может быть очень увлекательным, независимо от того, являются ли фигуры физическими формами или компьютерной графикой, занимается ли ребенок исследованием или решением проблемы, созданной взрослым.

Пространство

Контекст и обзор

Людям (и животным тоже) необходимы базовые представления о пространстве, если они хотят адекватно функционировать в повседневном мире. По этой причине маленькие дети (даже младенцы) часто сами по себе начинают использовать или развивать основные пространственные понятия, включая представления о местоположении, относительном положении, симметрии и направлении. Некоторые пространственные навыки и идеи встроены в систему человеческого восприятия: даже младенцы демонстрируют, что могут различать близкое и далекое, когда пытаются дотянуться до ближайшей из двух игрушек. Младенцы и малыши еще больше развивают эти способности, когда они ползают или ходят, осознают свое окружение и думают о том, куда они идут. Они знают, где находятся в пространстве и как перемещаться из одного места в другое. В знакомых местах, таких как дома и школы, они обычно знают, где что находится и как добраться до того, что им нужно. Они узнают, что мяч находится близко к стулу, что кукла находится под стулом и что самый быстрый путь к стулу — пройти под столом. Они учатся использовать слова для описания позиций, местоположений и направлений. Когда они становятся старше, они используют блоки и другие объекты для создания симметрий, которые иногда бывают красивыми, например, творение, показанное на рис. 8.0005

Несмотря на то, что их повседневные пространственные представления часто бывают полезными (как в случае с перемещением по знакомому окружению) и иногда удивительно мощными (как в случае со сложными симметриями), маленьким детям еще предстоит многому научиться, и им нужна помощь взрослых. двигаться вперед. Учителя и родители могут развить и расширить то, что маленькие дети уже знают о космосе. Взрослые могут помочь маленьким детям математизировать их повседневные представления о пространстве. Это включает в себя использование языка и различных представлений для описания и понимания пространственных идей.

Важность математического понимания пространства

Есть много причин для изучения пространства, так же как и для изучения формы и числа.

Космос интересен сам по себе.  Пространственные идеи включают следующее:

• Простое расположение и положение: собака находится сверху слона, и в то же время слон находится под собакой.
• Перспектива: с того места, где я сижу, я вижу кота слева и кита справа, а с того места, где вы сидите, напротив меня, вы видите кота справа и кита слева.
• Координаты на декартовой плоскости: пудель в четвертой строке и пятом столбце.
• Указания: ребенок может добраться до сундука с сокровищами, пройдя два шага вперед, повернув направо, а затем пройдя четыре шага вперед, после чего ребенок делает пол-оборота влево и проходит пять шагов по диагонали.
• Эстетические качества зеркальной симметрии: этот симметричный дизайн действительно красив, но этот асимметричный беспорядок — нет.

Каждая из этих тем сопряжена с трудностями: если мышь находится поверх кошки, которая находится поверх собаки, то кошка одновременно находится и поверх, и под чем-то другим. Детям трудно координировать два разных отношения (например, сверху и снизу), но взрослые могут помочь.

Пространственные идеи лежат в основе большей части нашего понимания математики. Чтобы понять сложение, ребенок может использовать идеи слияния двух отдельных групп объектов или прыжка вправо на стандартной числовой строке. Чтобы понять вычитание, ребенок может подумать об обезьянах, прыгающих с кровати. Чтобы понять эквивалентность, ребенок может представить себе балансировку предметов на весах. Чтобы понять умножение, ребенок может обратиться к областям или массивам точек. Действительно, представления о числе у детей и взрослых пронизывают пространственные метафоры и представления.

Пространственное понимание, язык и символы имеют практическую ценность . Дети (и взрослые) живут в космосе. Целенаправленное движение в нем требует прежде всего понимания пространственных отношений в повседневном окружении, например, когда малыш узнает, что чучело коровы находится за диваном. Позже ребенок учится и использует соответствующий пространственный язык, чтобы ориентироваться в мире (например, когда мама говорит: «Иди в гостиную и поищи под диваном своего игрушечного енота»). Еще позже чтение карты шоссе необходимо для того, чтобы добраться до пункта назначения. Взрослый использует идеи пространства, чтобы построить книжный шкаф или ковровое покрытие в комнате. Язык и символика позволяют нам превзойти повседневные пространственные знания животных.

Пространственные знания и язык предсказывают будущую успеваемость . Те дети, которые приобретают четкое понимание пространства и пространственного языка, как правило, демонстрируют более высокие математические достижения, чем учащиеся, которые не достигают такого мастерства.

Что детям нужно знать о космосе

У детей есть неформальные знания о пространстве , на котором может основываться раннее математическое образование. Они вполне способны узнать больше о следующих важных темах.

Базовое положение. Дети умеют находить предметы в окружающей среде. Они часто используют неформальный или расплывчатый язык, чтобы описать, где находятся вещи по отношению к другим вещам, включая самих себя. Но им нужно углубить свое понимание позиции и выучить правильные математические слова, чтобы говорить о ней.

Подумайте, как ребенок может указывать расположение предметов и людей в комнате.

• Я стою на столе.
• Я положил свою липкую конфету на белый лист.
• Я бросил огрызок яблока за дерево .
• Я положил свое нижнее белье под кровать.
• Я положил рассол в середине бутерброд.
• Мой стул ниже окна.
• В дно чаши есть крестовина.
• Я положил монету в свою копилку.

Все существительные в примерах относятся к вещам, классам объектов , которые ребенок может легко идентифицировать. Например, есть много видов яблок, и ребенок может легко научиться определять их все как яблоки. Но положения и места — это абстрактные идеи, и все они относительны. Например, рассол в середине бутерброда касается хлеба сразу сверху и снизу. Нижнее белье под ним соответствует кровати над ним.

Другой способ осмысления пространственных отношений заключается в том, что объекты служат ориентирами для рассматриваемого местоположения. Ориентир означает обозначение земли или указание объекта, который помогает определить местоположение. Даже маленькие дети могут использовать ориентиры, чтобы найти местонахождение спрятанного предмета. Например, если вы поместите игрушку за диваном, пока ребенок смотрит, он сможет найти игрушку позже: он знает, что игрушка находится за диваном. В этом случае игрушка — это объект, диван — ориентир, а отношение между ориентиром и объектом — 9.0103 сзади или сзади.  

Во всех этих случаях детям необходимо выучить две вещи: слова и понятия. Им нужно выучить позиционные слова, такие как над  или рядом с  , и им нужно знать понятия, к которым относятся эти слова. Например, слова рядом с  относятся к понятию, указывающему, что объект примыкает к другому различными способами, либо справа, либо слева от него. Вы можете помочь детям научиться развивать эти слова и понятия, моделируя. Например, если дошкольника спросить: «Где книжки с картинками?» она может ответить, сказав: «Вон там» и жестикулируя. Вы можете ответить: «Вы правы. Их на полке рядом с шкафом для верхней одежды.»          

Сложные позиции .  Левая и Правая общеизвестно трудны для изучения маленькими детьми, и им нужно много практиковаться с этими идеями. Во-первых, дети должны помнить, что одна рука находится справа, а другая слева. Эта идея усиливается, когда дети наклеивают наклейку на правую руку, а затем правильно обмениваются рукопожатием. Затем дети должны применить идею правой и левой к внешним объекты. Это особенно сложно, потому что эти понятия всегда связаны с направлением, в котором смотрит ребенок. Например, если Марио смотрит на стол с одного направления, он видит книгу справа и блок слева. перейдет к противоположной стороне стола, он увидит обратное. Дети вряд ли будут осваивать левое и правое, пока не станут старше, возможно, в начале начальной школы. Не зацикливайтесь на их первоначальной неудаче. 

Дошкольникам очень трудно понять двойственные отношения, принимать разные точки зрения одновременно. В нашем предыдущем примере огурец в бутерброде находится одновременно на над нижним куском хлеба и на под верхним куском. Как может огурец вынести двусмысленность — двойную идентичность или раздвоение личности — быть одновременно наверху и внизу? Поскольку дети склонны быть эгоцентричными, то есть смотреть на вещи и их отношения только с одной точки зрения, им трудно иметь дело с двойственными или, в более общем смысле, множественными отношениями. В этом дети похожи на рассол.

Другая задача, поиск объектов в двух измерениях, включает в себя простые двойные отношения между высотой и шириной. Предположим, ребенок видит сетку из единичных квадратов, которая идет вверх на пять делений и вбок на пять делений (и, конечно, имеет все соответствующие квадраты посередине).

Кто-то поместил объект на сетку, как показано на рисунке 9. Я прошу ребенка описать, где он находится, потому что я его не вижу. Она может сказать, что это там, но это не поможет. Она может сказать, что это выше этого квадрата, но это тоже не поможет. Она должна сказать что-то вроде этого: «Идите к нижнему квадрату слева. Затем идите на четыре клетки вверх и на две клетки вправо».

В повседневной жизни дети занимаются поиском или направленными видами деятельности. Например, в классиках нужно прыгать на разные квадраты в соответствии с набором чисел. Другим примером являются настольные игры, такие как Извините , в которых они могут двигаться вперед на определенное количество делений, а затем должны вернуться назад.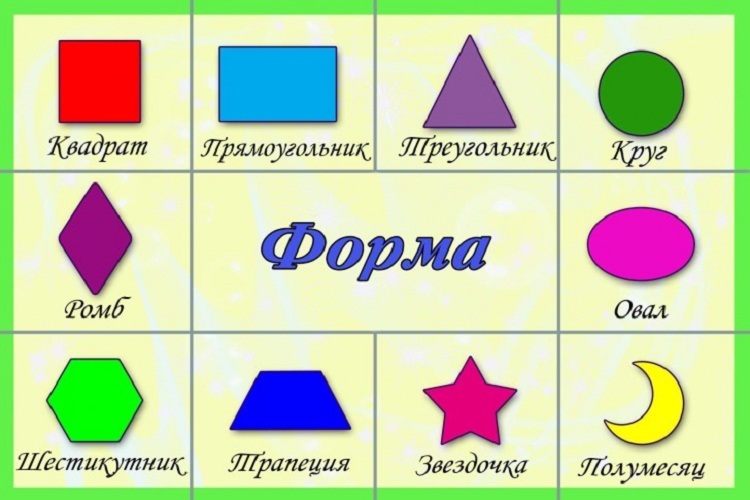

На уровне дошкольного образования учителя могут помочь детям стать более опытными в следовании указаниям местоположения и их понимании. Во время перекуса, например, учитель может сказать: «Когда мы накрываем стол для перекуса, мы ставим чашки рядом с тарелками, а сок ставим в середину стола, чтобы вы все могли его достать. И не забудьте положить салфетку на эту сторону каждой тарелки.

Сложные отношения также включают в себя еще одну важную математическую тему, симметрию , которая широко распространена в природе. Левое крыло бабочки является зеркальным отражением другого. Человеческое тело воплощает симметрии: левая рука является зеркальным отражением правой руки.

Математика определяет множество различных видов симметрии. Рассмотрим идею зеркального отображения, а именно, что симметрия делит фигуру пополам таким образом, что одна сторона имеет ориентацию, противоположную другой. Представьте, что у вас есть какая-то фигура на плоской поверхности. Вы держите зеркало вертикально рядом с фигурой. Затем у вас есть фигура и зеркальное отражение фигуры. Фигура и зеркальное отражение симметричны. Использование зеркала таким образом может помочь детям изучить и понять, что означает симметрия линий. Например, на рисунке 10 каждая фигура симметрична, а каждая линия является линией симметрии.

Дети постоянно создают двухмерные и трехмерные симметрии, играя с кубиками. На рис. 11 показан пример того, как ребенок может исследовать симметрию с помощью блоков узоров. Обратите внимание, что для того, чтобы сделать эту фигуру, ребенку пришлось вручную вращать некоторые блоки, например, красные трапеции, чтобы получить зеркальное отражение. Маленьким детям может потребоваться физически манипулировать объектами, чтобы правильно показать отражение. Кроме того, этот опыт может помочь ребенку позже развить способность видеть, как фигуры можно мысленно поворачивать или переворачивать, не создавая их.

Карты. Карты включают в себя особый вид символизма, показывающий, где вещи находятся по отношению друг к другу.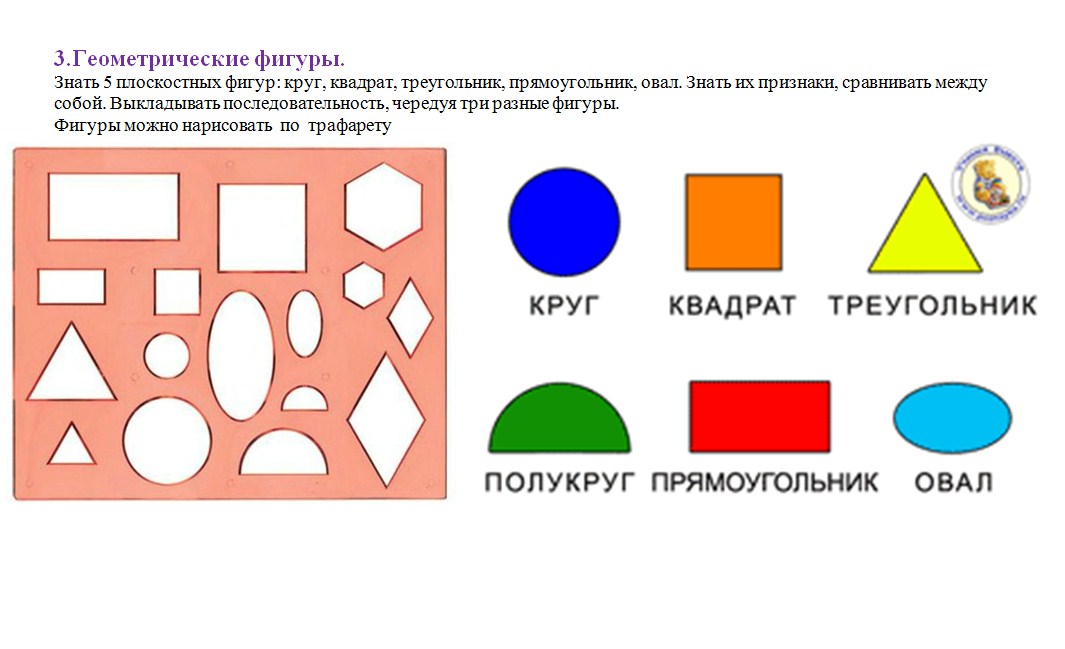 Вы можете представить класс разными способами. Вы можете описать это словами. Вы можете сфотографировать его. Вы можете сделать реалистичный рисунок. Вы можете создать его уменьшенную трехмерную модель. Вы можете создать его двухмерную карту с высоты птичьего полета, как показано выше. Вы можете создать его топографическую карту. Вы можете создать что-то вроде карты метро, ​​которая показывает относительное положение, но не точно фиксирует расстояния.

Прежде чем дети смогут понять, как выглядит их класс во всех этих различных аспектах, они должны понять точку зрения или перспективу. Раннее пространственное мышление младенцев и детей младшего возраста часто зависит от их собственной точки зрения. Ребенок мыслит положение предмета по отношению к своему положению в пространстве. Позже, когда дети осознают, что у них есть четкая точка зрения, они могут начать представлять, как выглядит пространство с других точек зрения. Например, ребенок может прийти к выводу, что то, как класс выглядит со своего стула, отличается от того, как класс выглядит со стула друга, или то, как класс выглядит со своего места на ковре, отличается от того, как выглядит класс. со стула, на котором сидит учитель во время коврика. Маленьким детям нелегко децентрироваться и визуализировать, как пространства выглядят с других точек зрения. Работа с картами и моделями может дать детям опыт, который поможет им увидеть пространство с других точек зрения.

Стандартные карты (хотя, возможно, и не топографические) сложны для понимания детьми, потому что они представляют трехмерную реальность в двухмерном пространстве, а также потому, что карта пропорционально меньше реальности. Дошкольники должны сначала научиться читать простые карты, например карту класса, а затем создавать их. Действия с картой могут проводиться во время круга, когда учитель может использовать карту, чтобы показать детям, где они должны сидеть, или в строю, когда карта может показывать, кто идет первым, вторым и так далее, чтобы ребенок мог определить как ее собственная позиция, так и ее друга.

Выводы по форме и пространству

Форма и пространство — фундаментальные математические темы, которые дети должны изучать. Им необходимо усвоить основные концепции, математизировать и развить свои повседневные знания, а также научиться передавать то, что они узнали. Изучение геометрии может быть глубже, чем думают многие взрослые, и может доставлять маленьким детям приятные интеллектуальные задачи.

Фоновое чтение

Клементс Д. Х. Геометрическое и пространственное мышление у детей младшего возраста. В Copley, JV (Ed.). (1999). Математика в ранние годы. Рестон, Вирджиния: Национальный совет учителей математики.

Дехане, С. (2011). Чувство числа: как разум создает математику (пересмотренное и обновленное изд.). Нью-Йорк: Издательство Оксфордского университета.

Сотрудничество по ранней математике в Эриксоновском институте. (2014). Большие идеи ранней математики: что должны знать учителя маленьких детей (Первое изд.). Бостон: Пирсон.

Хоуз, З., Тепило, Д., и Мосс, Дж. (2015). Развитие пространственного мышления: значение для раннего математического образования В Исследовательской группе Б.