Как объяснить ребенку задачу по математике 4 класс: Как подтянуть математику самостоятельно (4 класс) — 60 ответов

Содержание

ГДЗ: Математика 4 класс Башмаков, Нефедова

Часть 1. Страницы 6-7 Прибавляем по единице

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 8-9, Называем большие числа

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 10-11, Классы и разряды

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 12-13, Считаем устно и письменно

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 14-15, Называем, записываем, сравниваем

1 2 3 4 5 6 7 8 9 10 11 12

Часть 1. Страницы 16-17, Считаем деньги

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 18-19, Сколько человек на земле?

1 2 3 4 5 6 7

Часть 1. Страницы 20-21, Разворот истории

1 2 3

Часть 1. Страницы 22, Проверяем, чему мы научились

1 2 3 4

Часть 1. Страницы 22-25, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Часть 1. Страницы 26-27, Складываем и вычитаем разрядные слагаемые

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 28-29, Складываем круглые числа

1 2 3 4 5 6 7 8 9 10

Часть 1.

Страницы 30-31, Складываем и вычитаем тысячи и миллионы

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 32-33, Меняем число единиц в разряде

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 34, Проверяем, чему мы научились

1 2 3

Часть 1. Страницы 34-35, Математический тренажёр

1 2 3 4 5 6 7 8

Часть 1. Страницы 36-37, Складываем и вычитаем большие числа

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 38-39, Вычитаем из чисел с нулями

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 40-41, Свойства сложения

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 42-43, Вычисляем разными способами

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 44-45, Считаем в прямом и обратном порядке

1 2 3 4 5 6 7 8

Часть 1. Страницы 48, Проверяем, чему мы научились

1 2 3

Часть 1. Страницы 48-49, Математический тренажёр

1 2 3 4 5 6 7 8

Часть 1. Страницы 50-51, Метр и километр

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 52-53, Сравниваем, вычисляем, решаем задачи

1 2 3 4 5 6 7 8 9 10

Часть 1.

Страницы 54-55, Метр и сантиметр

1 2 3 4 5 6 7 8

Часть 1. Страницы 56-57, Меньше метра

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 58-59, Вычисляем периметр многоугольника

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 60-61, Переводим единицы длины

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 62-63, Геометрические задачи

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 64, Проверяем, чему мы научились

1 2 3 4

Часть 1. Страницы 64-67, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Часть 1. Страницы 68-69, Играем с Кенгуру

1 2 3 4 5 6 7 8 9 10 11 12

Часть 1. Страницы 72-73, Вспоминаем письменное умножение

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 74-75, Свойства умножения

1 2 3 4 5 6 7 8 9 10 11 12

Часть 1. Страницы 76-77, Умножаем круглые числа

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 80-81, Вычисляем площадь

1 2 3 4 5 6 7 8 9 10 11 12 13

Часть 1. Страницы 82, Проверяем, чему мы научились

1 2 3 4

Часть 1.

Страницы 82-83, Математический тренажёр

1 2 3 4 5 6 7 9 10 11 12

Часть 1. Страницы 84-85, Вспоминаем письменное деление

1 2 3 4 5 6 7 8

Часть 1. Страницы 86-87, Делим большие числа

1 2 3 4 5 6 7 8 9

Часть 1. Страницы 88-89, Свойства деления. Делим круглые числа

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 90-911, Находим неизвестное

1 2 3 4 5 7 8 9 10

Часть 1. Страницы 92, Проверяем, чему мы научились

1 2 3 4

Часть 1. Страницы 92-93, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 92-93, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 94-95, Делим числа с нулями

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 96-97, В частном 0?

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 98-99, Делим на круглое число

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 100-101, Вычисляем устно и письменно

1 2 3 4 5 7 8 9 10

Часть 1. Страницы 102, Проверяем, чему мы научились

1 2 3 4

Часть 1.

Страницы 102, Проверяем, чему мы научились

1 2 3 4

Часть 1. Страницы 102-105, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

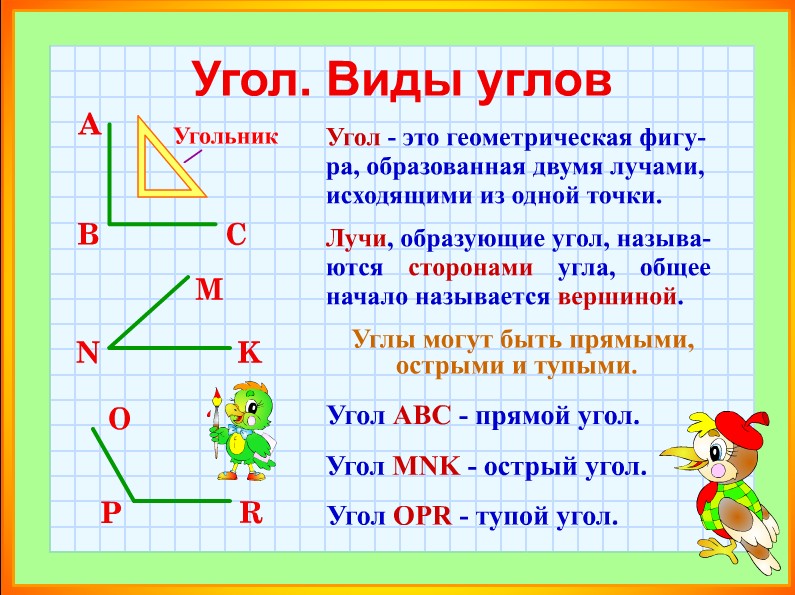
Часть 1. Страницы 106-107, Что изучает геометрия?

1 2 3 4 5 6 7

Часть 1. Страницы 108-109, Четырёхугольники

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 110-111, Решаем задачи

1 2 3 4 5 6 7 8 9 10

Часть 1. Страницы 114-115, Куб

1 2 3 4 5 6 7 8 9 10 11

Часть 1. Страницы 116-117, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Часть 1. Страницы 118-119, Играем с Кенгуру

1 2 3 4 5 6 7 8 9 10 11

Часть 2. Страницы 6-7, Масса и её измерение. Центнер

1 2 3 4 5 6 7 8 9 10

Часть 2. Страницы 8-9, Переводим единицы массы

1 2 3 4 5 6 7 8 9 10

Часть 2. Страницы 10-11, Ровно столько же

1 2 3 4 5 6 7 8 9 10

Часть 2. Страницы 12, Проверяем, чему мы научились

1 2 3

Часть 2. Страницы 12-13, Математический тренажёр

1 2 3 4 6 7 8 9

Часть 2. Страницы 14-15, Умножение многозначных чисел.

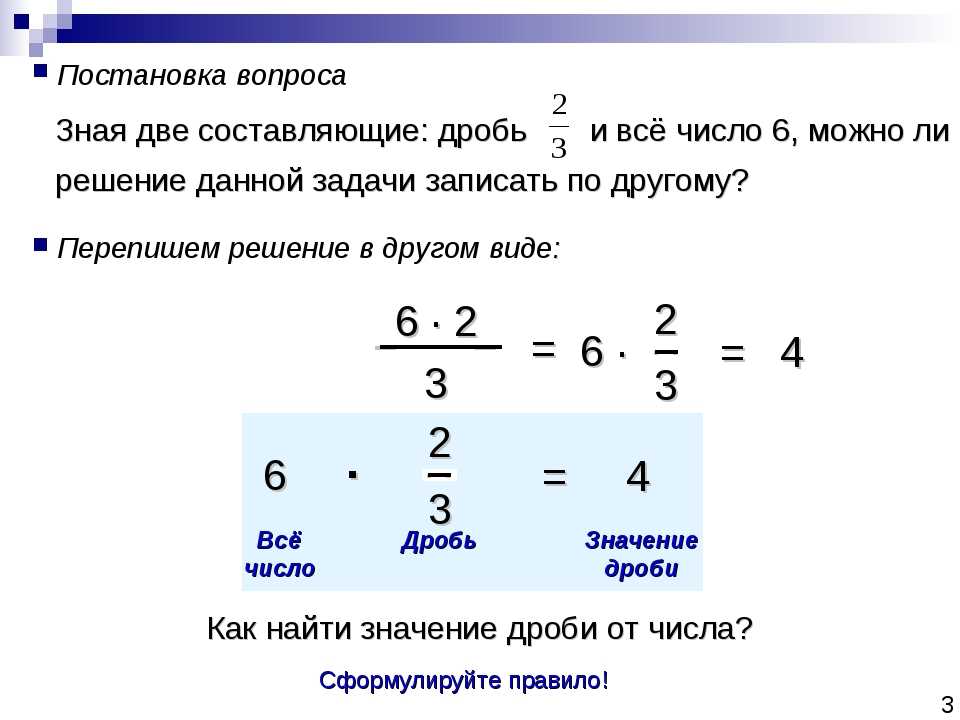Как умножают на двузначное число

1 2 3 4 5 6 7 8 9 10

Часть 2. Страницы 16-17, Умножаем круглые числа

1 2 3 4 5 7 8

Часть 2. Страницы 18-19, Приёмы умножения

1 2 4 5 6 7 8 9

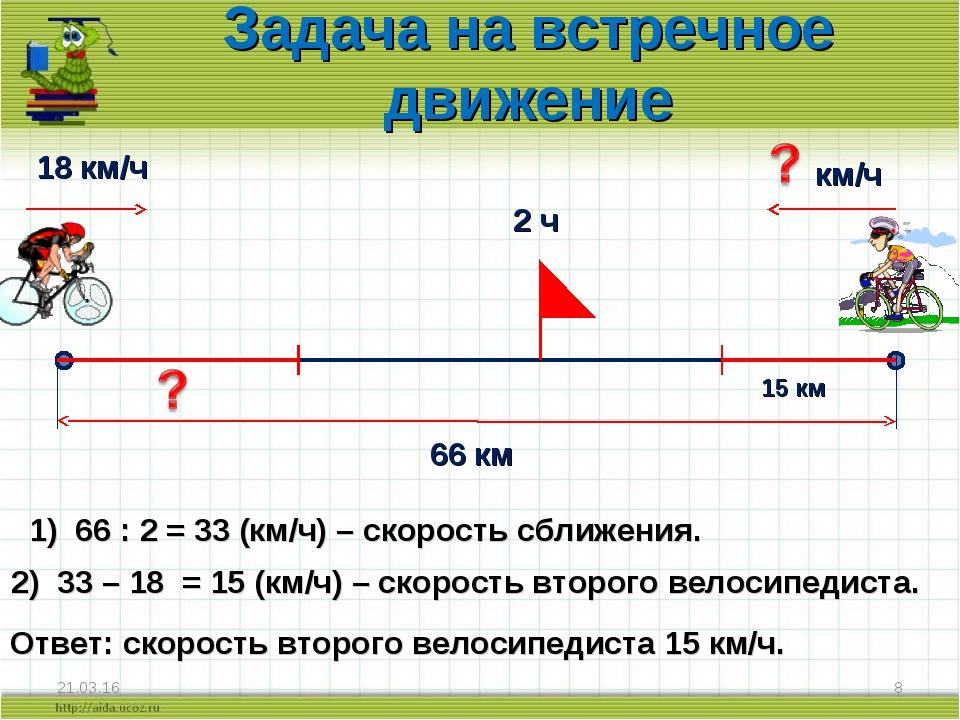
Часть 2. Страницы 20-21, Движение в противоположных направлениях

1 2 4 5 6 7 8 10

Часть 2. Страницы 22, Проверяем, чему мы научились

1 2 3

Часть 2. Страницы 22-23, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11

Часть 2. Страницы 24-25, Умножаем на трёхзначное число

1 2 3 4 5 6 7 8

Часть 2. Страницы 26-27, Тренируемся в логике

1 2 4 5 6

Часть 2. Страницы 28-29, Проверяем, что узнали

1 2 3 4 5 6 7 8 9 10

Часть 2. Страницы 34, Проверяем, чему мы научились

1 2 3

Часть 2. Страницы 34-37, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

Часть 2. Страницы 38-39, Площадь и её измерение. Квадратный метр

1 2 3 4 5 6 7 8 9

Часть 2. Страницы 40-41, Меньше квадратного метра

1 2 3 4 5 6 7 8 9 10 11

Часть 2.

Страницы 42-43, Составляем таблицу единиц площади

1 2 3 4 5 6 7 8 9 10 11

Часть 2. Страницы 44-45, Измерение больших участков

1 2 4 5 6 7 8

Часть 2. Страницы 46, Проверяем, чему мы научились

1 2

Часть 2. Страницы 46-47, Математический тренажёр

1 2 3 4 5 6 7 8 9

Часть 2. Страницы 48-49, Деление многозначных чисел. Деление — действие, обратное умножению

1 2 3 4 5 6 7

Часть 2. Страницы 50-51, Делим с остатком

1 2 3 4 5 6 7 8 9 10

Часть 2. Страницы 52-53, Что в частном?

1 2 3 4 5 6 7 8 9 10

Часть 2. Страницы 54-55, Оцениваем частное

1 2 3 4 5 6 7 8 9

Часть 2. Страницы 56, Проверяем, чему мы научились

1 2 3

Часть 2. Страницы 56-59, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Часть 2. Страницы 60-61, Скорость

1 2 3 4 5 6 7 8

Часть 2. Страницы 62-63, Производительность труда

1 2 3 4 5 6 7 8

Часть 2. Страницы 64-65, Делим на трёхзначное число

1 2 3 4 5 6 7 8 9 10

Часть 2.

Страницы 66-67, Оцениваем результат вычислений

1 2 3 4 5 6 7 8 9

Часть 2. Страницы 68, Проверяем, чему мы научились

1 2 3

Часть 2. Страницы 68-71, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Часть 2. Страницы 72-73, Время и его измерение. Единицы времени

1 2 3 4 5 6 7 8 9

Часть 2. Страницы 74-75, Календарь и часы

1 2 3 4 5 7 8 9

Часть 2. Страницы 76-77, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13

Часть 2. Страницы 78-79, Играем с Кенгуру

1 2 3 4 5 6 7 8 9 10 11

Часть 2. Страницы 80-81, Работа с данными. Представление информации

1 2 3 4 5 6

Часть 2. Страницы 82-83, Таблицы

1 2 3 4 5 6 7

Часть 2. Страницы 84-85, Диаграммы

1 2 3 4 5 6

Часть 2. Страницы 86-87, Планирование

1 2 3 4 5 6

Часть 2. Страницы 88-89, Контроль и проверка

1 2 3 4 5 6 7

Часть 2. Страницы 90-91, Математический тренажёр

1 2 3 4 5 6 7

Часть 2. Страницы 94-95, Числа и величины. Запись чисел

1 2 3 4

Часть 2.

Страницы 96-97, Сравнение чисел

1 2 3 4

Часть 2. Страницы 98-99, Задачи на сравнение:

1 2 3 4 5 6 7

Часть 2. Страницы 100-101, Масса и вместимость

1 2 3 4 5 6

Часть 2. Страницы, Время

1 2 3 4 5 6

Часть 2. Страницы 104, Проверяем, чему мы научились

1 2 3 4

Часть 2. Страницы 104-107, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Часть 2. Страницы 108-109, Арифметические действия. Сложение и вычитание

1 2 3 4 5 6 7

Часть 2. Страницы 110-111, Умножение и деление

1 2 4 5 6 7 8

Часть 2. Страницы 112-113, Числовое выражение

1 2 3 4 5 6 7

Часть 2. Страницы 114-115, Свойства арифметических действий

1 2 3 4 5 6 7

Часть 2. Страницы 116-117, Способы проверки вычислений

1 2 3 4 5 6

Часть 2. Страницы 118, Проверяем, чему мы научились

1 2 3

Часть 2. Страницы 118-119, Математический тренажёр

1 2 3 4 5 6 7 8 9 10 11

Часть 2. Страницы 120-121, Фигуры и величины. Распознавание геометрических фигур

1 2 3 4

Часть 2.

Страницы 122-123, Построение геометрических фигур

1 2 3

Часть 2. Страницы 124-125, Длина

1 2 3 4 5

Часть 2. Страницы 126-127, Площадь

1 2 3 4 5

Часть 2. Страницы 128, Проверяем, чему мы научились

1 2 3

Часть 2. Страницы 128-129, Математический тренажёр

1 2 4 5 6 7 8 9 10 11

Часть 2. Страницы 130, Решение текстовых задач. Задачи на стоимость

1 2 3 4 5

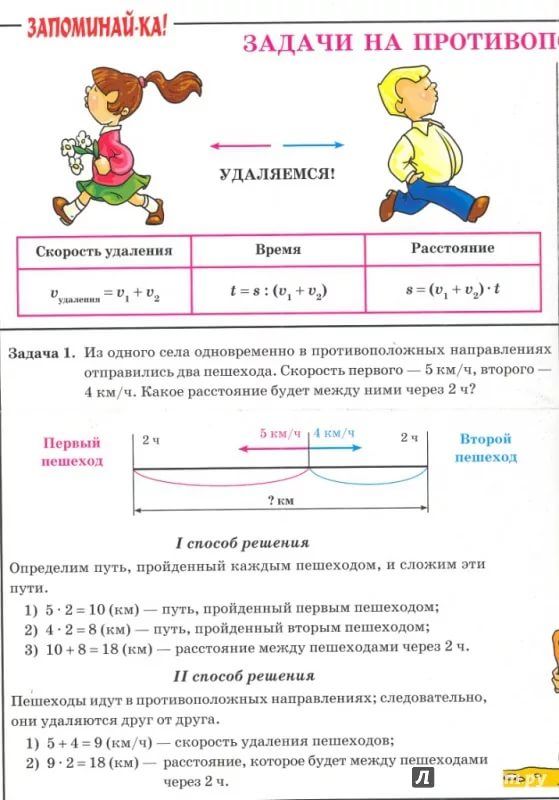
Часть 2. Страницы 131-134, Задачи на движение

1 2 3 4 5

Часть 2. Страницы 135, Задачи на производительность

1 2 3 4 5 7 8 9

Часть 2. Страницы 136-137, Задачи на доли

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Часть 2. Страницы 140-142, Умеешь ли ты…

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Часть 1. Страницы 6-7 Прибавляем по единице: 1

Предыдущее

Следующее

Условие

Решебник №1

Решебник №2

Предыдущее

Следующее

Как научиться решать задачи ✅ Блог IQsha.ru

Ни один человек не умеет с рождения решать математические задачи.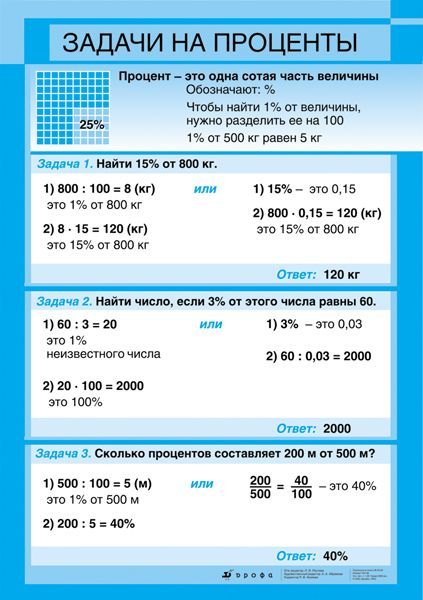 Но этому можно и нужно научиться. Чтобы быстро и правильно решать задачи, нужно знать и выполнять несколько важных условий. В этой статье мы расскажем об этих “секретных ингредиентах”, которые позволят ребенку постичь таинство быстрого решения математических задач.

Математика — это нестрашно

Многие дошкольники боятся математики как страшного чудовища, которое мучает непонятными условиями и решениями. Эти страхи навязаны взрослыми, упрекающими своё чадо в нежелании заниматься или ругающими за неверные ответы. Первая задача взрослых — не напугать предметом, а показать, что математика — это нестрашно.

Чтобы “царица наук” приносила только положительные эмоции, каждый день постарайтесь обращать внимание ребёнка на самые простые признаки этого предмета. Математика окружает нас везде: мы считаем в магазине деньги, смотрим номера домов на улице, вычисляем время, которое нам нужно для поездки, и многое-многое другое. В время прогулки с малышом предложите решить вместе весёлую задачку: узнать, сколько шагов до ближайшего дерева или качели. Также обратите внимание ребёнка на пользу математики в решении самых обычных дел.

Если ваш малыш не проявляет интерес к математике и его больше интересуют гуманитарные науки, не стоит огорчаться и принуждать к занятиям. Начните давать посильные задачи: например, пересчитать гостей и принести нужное количество вилок на стол, или определить, в какой тарелке больше фруктов. После выполнения задания обязательно похвалите ребёнка и отметьте, что он отлично справился с задачей. Так малыш поймет важность и необходимость математических знаний.

Выполните развивающие упражнения от Айкьюши

Как решить задачу

Прозвенел первый звонок, и теперь ваш малыш настоящий школьник! Математика — один из самых главных уроков, на котором ребёнка будут ждать цифры, числа, фигуры, примеры и, конечно, задачи. Ведь именно в процессе решения любых математических задач ребёнок развивает логическое мышление, воображение, память, внимание и самоконтроль.

Умение быстро решать задачи для 1 класса по математике — очень важный навык. Освоив его, ребёнок будет легче понимать задачи и в старших классах, поэтому стоит запастись терпением и помочь малышу хорошо разобраться в этом вопросе, чтобы потом он решал задачи по математике самостоятельно. Согласитесь, лучше приложить немного больше усилий в 1 классе, чтобы потом не делать с ребёнком математику все школьные годы?

Учимся решать задачи

Алгоритм решения задач

Решать задачи ребёнку придётся всю школьную жизнь, и не только математические, но и по физике, химии, биологии. Именно поэтому с начальных классов стоит усвоить алгоритм решения, который применим к абсолютно любой задаче:

Читаем условие задачи
Первый раз ребёнок читает условие задачи вслух, затем ему нужно ещё раз прочитать задачу внимательно и не торопясь. Чтобы проверить понимание, попросите малыша пересказать условие задачи. Если он что-то забыл, спокойно задайте наводящий вопрос. Очень важно, чтобы у ребёнка не возникало затруднений в представлении объектов задачи.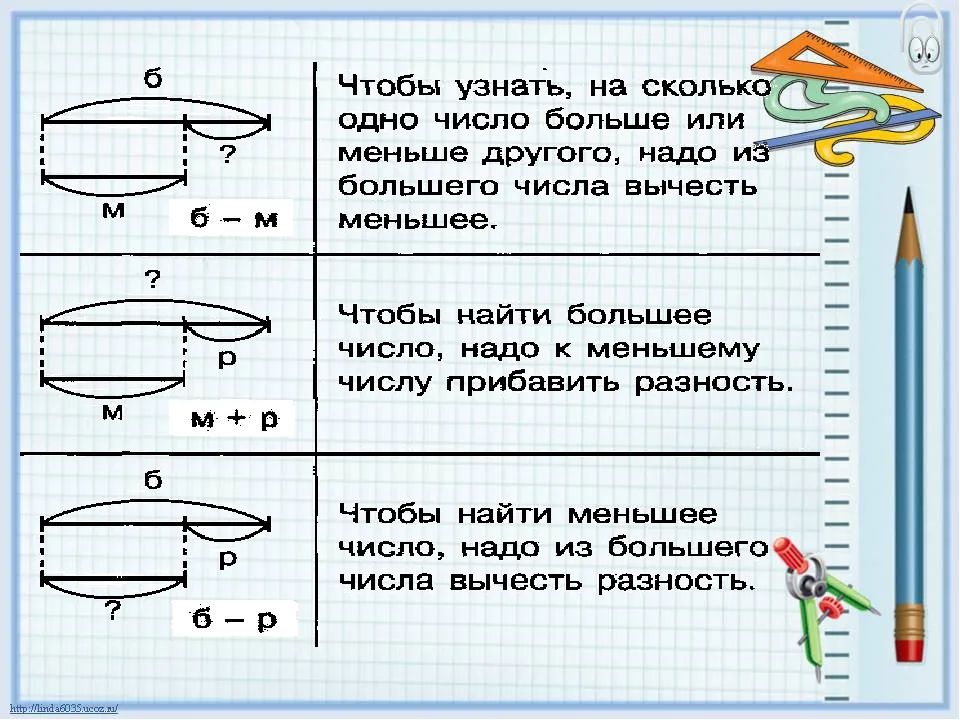 Если малыш не понимает какие-то слова в условии, обязательно расскажите и подробно объясните. Дайте ребёнку возможность прочитать условие столько раз, сколько нужно, не ругайтесь и не нервничайте, а лучше похвалите и подбодрите в этом старании.
Представляем задачу
Разобравшись с условием и усвоив все объекты в задаче, переходите к её схематическому представлению. Это можно сделать в виде рисунка или схемы, используя игрушки и реальные предметы. Например, если речь идёт о вазе с конфетами, можно взять несколько карамелек и разложить их по стаканам. Задачи на движение можно нарисовать схематично: домик, велосипед, дорогу и рядом изобразить знаки вопроса. Чем лучше и нагляднее будет нарисована задача, тем проще будет представить, какие действия нужно сделать для её решения. Возможно, уже в ходе создания рисунка ребёнок сможет решить задачу.
Детям в начале школьной жизни ещё очень сложно представлять задачу только в уме, абстрактно. Малышам гораздо легче и проще решать задачи, когда можно увидеть все объекты на рисунке или потрогать и переложить их.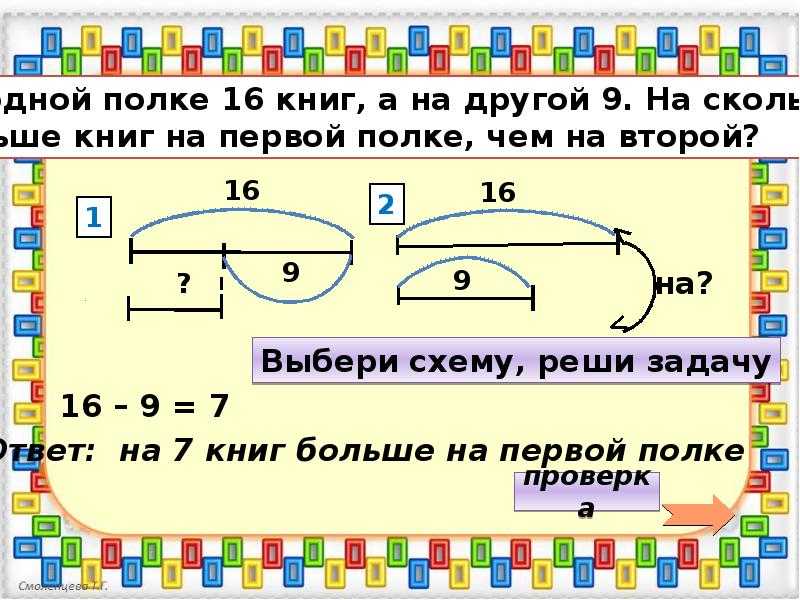 С возрастом ребёнок научится “видеть” задачу в голове, но сначала ему нужно понять, как это делается.
Решение задачи
Теперь можно переходить к решению. “Увидев” задачу, малыш уже может понять, какие действия нужно совершить, чтобы получить ответ. Если ребёнок не смог сразу найти решение, не нервничайте, а начните задавать наводящие вопросы, обращайте внимание на детали и обязательно хвалите. Малыш старается решить, а это уже большое дело! Не концентрируйтесь на текстовом условии, а используйте любые способы: инсценировка задачи, наглядное представление из подручных предметов, схема или рисунок.
Если в задаче нужно выполнить несколько действий, помогите малышу разложить задачу на несколько простых шагов. Такой способ поможет ребёнку увидеть закономерность и последовательность действий.
Записываем решение
Когда малыш уже полностью понял задачу, увидел все действия, которые нужно совершить, только после этого приступайте к записи решения.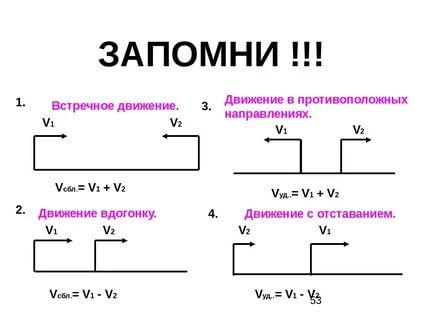 Подробно записывайте и проговаривайте вслух всё, что фиксируется в тетради. Это поможет ребёнку быстрее запомнить последовательность записи решения.
Если решение состоит из нескольких действий, то после вычислений ребёнку нужно обязательно записывать, что обозначает каждое число, чтобы в итоге не перепутать огурцы с грибами.
Ответ
Как только все вычисления сделаны и записаны, нужно сформулировать и зафиксировать на бумаге ответ. Для этого возвращаемся к условию задачи. Попросите малыша прочитать вопрос в задаче, а потом развернуто дать ответ. Например, если вопрос звучит так: “Сколько яблок съел Дима?”, ребёнку нужно ответить не просто “6 яблок”, а подробно — “Дима съел 6 яблок”, а потом записать этот развернутый ответ в тетрадь. Таким образом видно, что принцип формирования ответа заключается в вопросе, но без использования числительного. Конечно, первокласснику можно объяснить проще: “Вместо слова “сколько” говорим число и получаем развёрнутый ответ”.
Проверка
Задача решена! Похвалите ребёнка за все старания и усилия, ведь он смог решить математическую задачу, но не забывайте о проверке решения. Выполняя проверку, ребёнок учится очень важным навыкам — контролю и самоконтролю.
Не пугайте малыша, что теперь нужно ещё раз что-то решать, просто заинтересованно спросите: “Как ты думаешь, это правильный ответ? Давай проверим!”.

Выполнять проверку можно несколькими способами:

а) Сверка ответа
Самый простой способ — это посмотреть ответ в конце учебника. Но такой способ не всегда хорош и полезен, потому старайтесь пользоваться им нечасто.

б) Прикидка ответа
Прочитав условие задачи, ребёнок прикидывает, в каких пределах должен получиться ответ. Например, решая задачу, где нужно сложить 10 яблок и 15 груш, малыш задаётся вопросом: может ли получиться ответ меньше 10? В этом способе есть свои преимущества, но он менее точный.

в) Решение задачи другим способом
Такой способ хорош для более сложных задач, когда ребёнок уже достаточно хорошо ориентируется в действиях и умеет представлять условие. Однако к этому способу не стоит обращаться в самом начале обучения решению задач.

г) Подстановка результата в условие задачи
Именно так стоит обучать ребёнка проверке решения. Способ подходит для самых лёгких и первых задач по математике 1 класса.

Со временем вы можете показать малышу разные способы проверки решения задач, но не используйте все способы сразу. Это может только запутать первоклассника.

‍

Учимся решать задачи до 20

Очень важно, чтобы ребёнок четко усвоил алгоритм решения задач. Для этого старайтесь решать по одной задаче, не смешивая их с примерами или выполнением домашнего задания по другим предметам. Дайте малышу отдохнуть после решения, тогда новая информация хорошо усвоится и не забудется.

На нашем сайте в разделе Решаем задачи и примеры вы найдёте не только задачи и примеры по математике для 1 класса, но и для других классов начальной школы и даже для дошкольников. Ребёнок может выполнять задания для 1 класса как самостоятельно, так и вместе с вами. Кроме этого, малыш может оттачивать математические навыки в тренировке Математик, которая обновляется каждый день.

Решаем и составляем задачи 1 класс

Задачи в два действия 2 класс

Задачи на умножение и деление 3 класс

Задачи на движение 4 класс

Также рекомендуем вам нашу статью «Математические головоломки с ответами». Занимайтесь математикой в игровой форме!

Ольга Шадрина,
практикующий педагог-дефектолог, автор упражнений и обучающих материалов IQsha.ru

Объяснение ответов по математике: как помочь учащимся объяснить свое мышление

Случалось ли вам когда-нибудь просить учащегося объяснить свой ответ по математике, а вы получали пустой взгляд, быстрое изменение ответа или ответ: « Я просто это было в моей голове» ? Честно говоря, каждый год мои ученики почти так начинают учебный год. Но благодаря целенаправленному обучению я могу добиться, чтобы к концу года даже те ученики с пустым взглядом объясняли свои ответы полными предложениями с использованием математической лексики.

Хотите посмотреть, как я это делаю? Продолжайте читать мои лучшие советы, чтобы ваши ученики объяснили свои ответы по математике.

В этот пост включены партнерские ссылки, если вы хотите приобрести упомянутые книги по профессиональному развитию.

1. Разговоры о числах

Разговоры о числах — отличный способ развить чувство числа, заставить учащихся думать о математике по-новому и, конечно же, помочь им объяснить свои ответы. Если вы не знакомы с числовыми разговорами, они имеют следующий формат:

Учитель размещает задачу или серию задач на диаграмме.
Учащиеся решают задачу в уме.
Учитель призывает учеников дать ответы и записывает все полученные ответы.
Учитель призывает учащихся объяснить, как они получили ответы.
Учащиеся делятся всеми стратегиями, которые они использовали для получения правильного ответа, которые учитель записывает и перефразирует по мере необходимости.

Этот учебный инструмент является мощным, потому что учащиеся регулярно объясняют, как они получили свои ответы, и они регулярно слушают математические рассуждения и объяснения других учащихся.

Дополнительная литература: Числовые беседы Шерри Пэрриш

2. Постановка задачи + запись или публикация стратегий и объяснений учащихся

Я использовала эту стратегию в своей комнате в течение многих лет, чтобы помочь своим ученикам обдумывать, решать и объяснять текстовые задачи. . В основном, я ставлю словесную проблему или ситуацию. Мы читаем и обсуждаем проблему вместе, следя за тем, чтобы у всех учащихся была точка доступа или точка входа (в основном способ начать решение проблемы).

Студенты самостоятельно решают задачу, пока я хожу по комнате, создавая последовательность, чтобы поделиться работой студентов и объяснениями, которые затем проецируются на документ-камеру для просмотра всеми студентами. Видеть и слышать работы, мысли и объяснения других учеников очень полезно для всех моих учеников.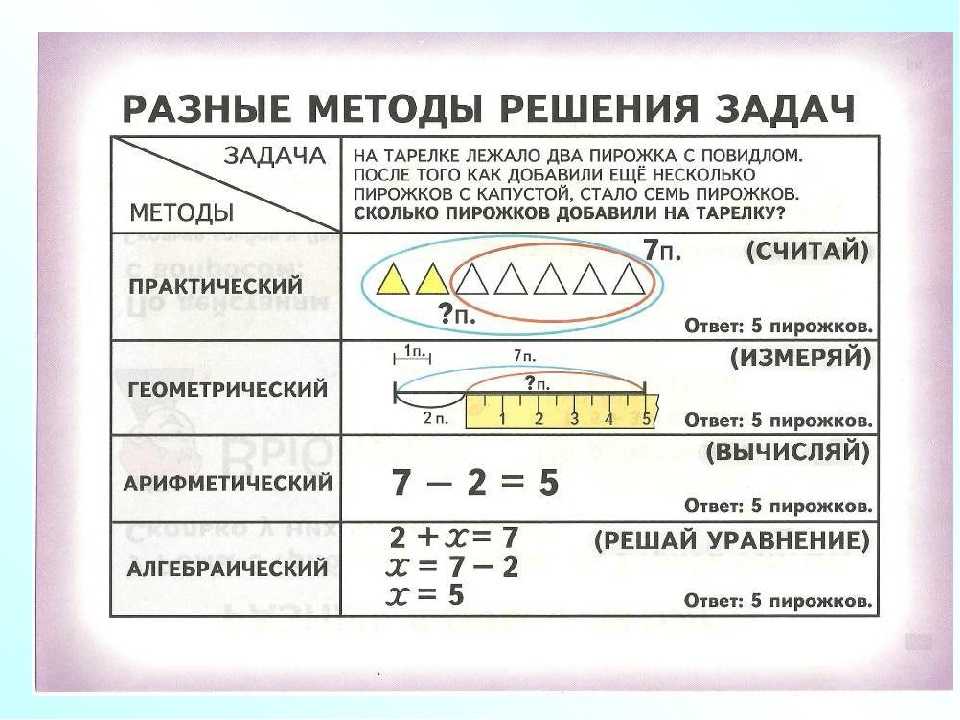

Дополнительная литература: Нажмите здесь, чтобы узнать больше об этой стратегии.

Если вам нужны текстовые задачи, чтобы решить задачу дня в вашем классе, нажмите здесь, чтобы увидеть мою задачу дня для 5-го класса (скоро будет 4-й класс).

3. Основы предложений

Основы предложений — отличный способ поддержать учащихся, особенно тех, кому трудно объяснить свои ответы или свое мышление. Вот мои основные предложения для объяснения ответов по математике.

Мой ответ… Я понял это…
Мой ответ… Чтобы получить ответ, я…
Мое решение… Я пришел к этому решению…
Чтобы получить ответ, я…
Сначала я…, Потом я…, Далее я…, Наконец, я…
Для начала я…
Первый шаг, который я сделал, был…
Эта проблема напомнила мне о…, поэтому я…
Я заметил…, поэтому я…
Я решил сложить/вычесть/умножить/поделить, потому что проблема…

Щелкните здесь или на изображении, чтобы загрузить копию этих основ предложений, которые помогут вашим учащимся объяснить свое математическое мышление.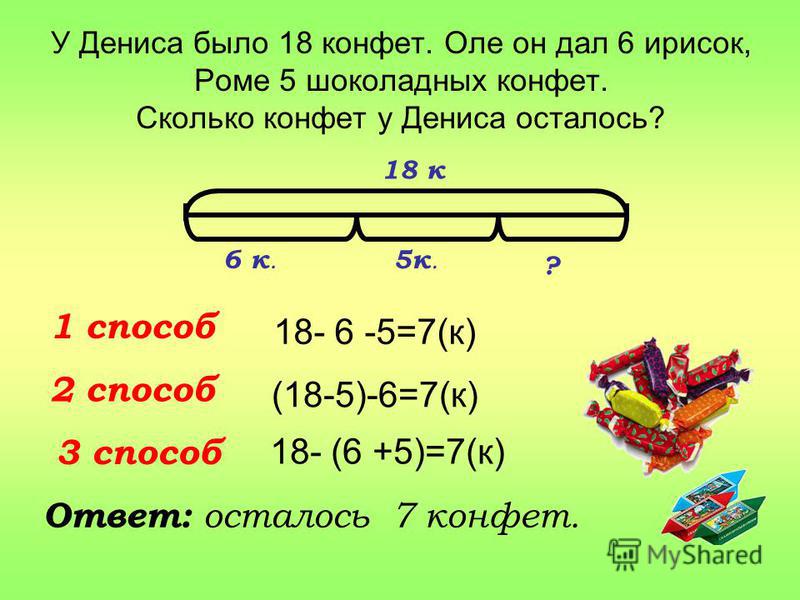 Их можно дать учащимся, чтобы они вклеили их в интерактивную математическую тетрадь в рамках урока по использованию стеблей. Их также можно превратить в якорную диаграмму.

Я также использую эти два примера, когда представляю основу предложения и рассказываю о том, как ее использовать. Один из примеров объясняет ответ на текстовую задачу, а другой объясняет ответ на вычислительную задачу. Они находятся в той же загрузке, ссылка на которую приведена выше.

4. «Переверни и поговори» или «Думай и поделись» ежедневно

Если учащиеся не рассказывают о том, как они решили проблему, или не объясняют свою работу, то, скорее всего, они не смогут написать об этом. Я ежедневно использую в своем классе «покажи и поговори» / «думай в паре», чтобы мои ученики говорили о математике.

В моем классе мы ежедневно обмениваемся устными объяснениями, а затем также записываем наши объяснения по крайней мере раз в неделю. Для этой цели я использую свой интерактивный блокнот с задачами по математике.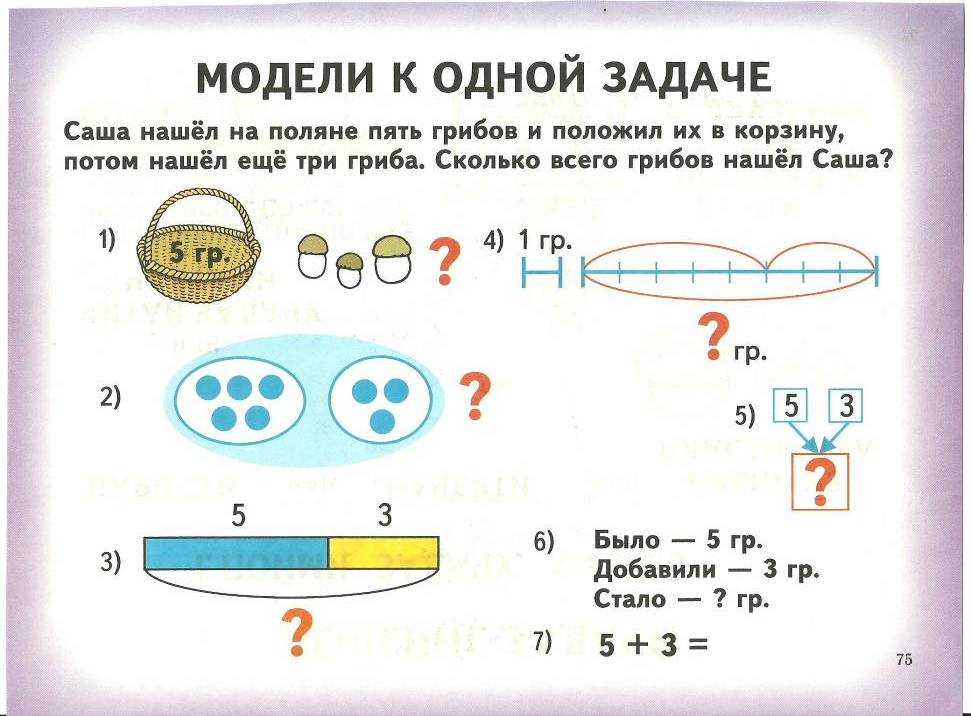

У меня есть задача по одному слову для каждого стандарта, поэтому я легко могу выполнять ее каждую неделю. Тот факт, что они размещены в наших интерактивных математических тетрадях, делает их отличным инструментом, к которому учащиеся могут обращаться.

Нажмите здесь, чтобы увидеть интерактивные задачи по математике, которые есть в моем магазине.

5. Моделируйте и перефразируйте

Когда вы обсуждаете математику со своими учениками, регулярно моделируйте, используя математический словарь для объяснения ответов. Если они не будут регулярно слышать правильный математический язык и словарный запас, то они не смогут использовать их сами.

В дополнение к моделированию перефразируйте ответы учащихся по мере необходимости, чтобы обеспечить ясность и точность. Вот какой язык вы можете использовать, когда перефразируете:

Я думаю, вы говорите… Это правильно?
Итак, ты… а потом ты… Верно?
Можете ли вы еще раз рассказать мне, как вы ________?
Можете ли вы повторить, как вы это сделали, но попробуйте использовать слова ___________ и ____________?

6.

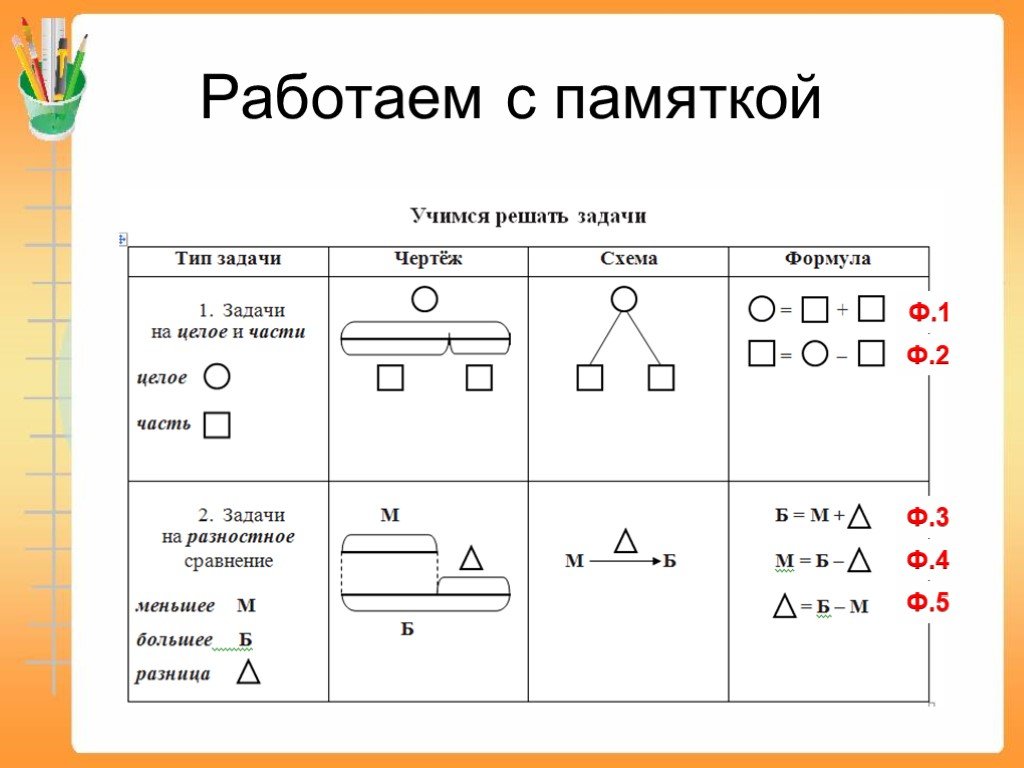Примеры для наставников

Мы постоянно используем тексты для наставников в наших обычных инструкциях по письму, и они так же хорошо помогают учащимся объяснять и писать по математике. Используйте примеры математических объяснений наставника, чтобы помочь учащимся увидеть то, что вы ожидаете, и помочь им сформулировать свои собственные объяснения.

Вот несколько способов собрать или создать примеры наставников для математических объяснений:

Создайте свои собственные примеры.
Используйте выпущенные примеры оценки состояния.
Поделиться текущими или предыдущими работами учащихся (с разрешения).

Нажмите здесь, чтобы загрузить два примера наставника, приведенные в Совете №3, которые показывают учащимся, как использовать основы предложений.

7. Переучить операции Концептуально

Одна из основных причин, по которой учащиеся не могут объяснить свою работу по математике, заключается в том, что у них нет концептуального понимания того, что они делают. На самом деле я трачу довольно много времени на «обучение на уровне класса», возвращаясь к 4-му или даже 3-му классу и переучивая концепцию концептуальным способом. Иногда я немного отстаю в своем темпе, но могу ускориться позже, когда мои ученики намного быстрее осваивают навыки уровня своего уровня.

Концептуальное обучение операциям действительно помогает моим ученикам объяснить свои ответы, потому что они точно знают, почему они складывают, вычитают и т. д.

Чтобы узнать больше о том, как я делаю это с ситуациями по сравнению с ключевыми словами, нажмите здесь.

8. Word Bank

Я обнаружил, что мои ученики с трудом объясняли, почему они решили выполнить ту или иную операцию. Им очень помогло создание банка слов математических фраз для каждой операции. Вот пример:

Нажмите здесь, чтобы получить копию этого плаката по математике. Есть три версии, и каждая версия увеличивается в разнообразии и сложности.

Мне пришлось моделировать это несколько раз, прежде чем они смогли сделать это самостоятельно. Чтобы смоделировать это, я спрашивал студентов, какая из фраз лучше всего описывает, почему они выбрали эту операцию. Затем я бы попросил их сказать мне, почему эта фраза совпадает. После этого я моделировал то, что они сказали, в 1-2 предложениях, используя контекст слова «проблема» и фразу из таблицы.

Вот пример: я умножил, потому что мешков с конфетами было равных групп. Кроме того, проблема заключалась в запросе суммы, поэтому мне нужно было объединить равные группы . Пакеты были группами, и количество конфет в каждом пакете было одинаковым.

9. Разнообразие задач для объяснения: вычисления и текстовые задачи

Мои ученики практикуются в объяснении как вычислительных задач, так и текстовых задач. Обычно я начинаю с объяснения того, как они решили вычислительную задачу, а затем перехожу к объяснению текстовых задач. Если они не могут объяснить шаги, которые они предприняли для решения вычислительной задачи, то объяснение того, как и почему они решили задачу со словами, вероятно, станет для них огромной проблемой.

10. Объяснения партнера

Еще один способ помочь учащимся, когда они только учатся объяснять свои ответы, используя сложную лексику и математический язык, — использовать объяснения партнера. Попросите партнеров решить проблему или задачу вместе, а затем вместе объясните свой ответ. Вы даже можете дать им два разных цветных карандаша или маркера, чтобы они написали объяснения. Это позволит вам быстро проверить, какие партнеры предоставляют какую информацию в окончательном объяснении.

11. Задайте наводящие вопросы: Что вы сделали в первую очередь? Следующий?

Когда ваши ученики затрудняются, задавайте открытые вопросы, чтобы помочь им в объяснении. Вот некоторые из моих вопросов:

Что вы сделали в первую очередь?
Что ты сделал дальше?
Что заставило тебя это сделать?
Зачем ты это сделал?
Откуда вы знаете, что ваш ответ правильный?
Откуда ты это знаешь?
Какой математический словарь мы можем включить в наше объяснение?

Вопросы такого типа помогут учащимся подумать о своем мышлении и дадут им словесную практику с объяснением. И помните из совета № 4, если учащиеся не могут вербализовать свои объяснения, то, скорее всего, они не смогут их написать.

12. Встроить в математические центры.

Самый простой способ попрактиковать это — попросить их выбрать одну задачу или проблему, которую они решили для объяснения. Вы можете делать по одному на математический центр или по одному в день.

12. Регулярно говорите о математике в классе.

Лучший способ (оставленный напоследок) научить ваших учеников объяснять свои ответы по математике — это регулярно использовать и продвигать математические разговоры в классе. Я планирую написать новый пост на эту тему в будущем, но вы можете ознакомиться с этим предложением по дальнейшему чтению, если вам интересно узнать об этом сейчас.

Дополнительная литература: Преднамеренная беседа: как структурировать и вести продуктивные математические дискуссии

Помощь в переходе от устных объяснений к письменным

Вот мои основные стратегии, которые помогут учащимся перейти от устных объяснений к письменным.

1.) Когда учащийся объясняет свои мысли или свой ответ, запишите основные ключевые слова, которые они произносят, в своего рода банк слов. Затем перескажите ученику, что вы слышали от него, и указывайте на каждое слово, когда вы его произносите. Наконец, попросите их записать свои мысли, используя некоторые или все ключевые слова, которые вы для них записали.

2.) Иногда мне приходится поддерживать сложность задач. Если я хочу, чтобы мои ученики действительно научились объяснять свои ответы, им должно быть достаточно комфортно с математикой, которую они выполняют. Для многих учеников работа над объяснением ответов при работе над сложной задачей на уровне класса может оказаться слишком сложной. Сначала помогите им научиться объяснять свои ответы с помощью навыков повторения, а затем перенести это в навыки и задачи уровня своего класса.

Я надеюсь, что эти предложения помогут вашим ученикам, когда они будут объяснять ответы и свои математические действия, а также размышлять над этими ответами. Дайте мне знать, если у вас есть какие-либо вопросы по любому из советов в комментариях.

Сохранить

. Выберите номера и вопрос!

Я уверен, что мы все видели, как это происходило в тот или иной момент на уроке математики. Мы даем учащемуся решить сюжетную задачу, и после беглого просмотра учащийся вытаскивает числа из задачи, вычисляет их и записывает ответ.

Если ответ правильный, мы предполагаем, что учащийся понял концепцию. Однако, если это неверно, у нас остается длинный список вопросов: понимают ли они, что их ответ не имеет смысла? Они не поняли контекста? Они просто брали цифры и работали, чтобы просто закончить, или они действительно не знали, что с ними делать? Самое главное, мы спрашиваем себя, как я могу помочь учащимся осмыслить то, что они читают, и обдумать логику своего ответа в контексте проблемы?

Если нам повезет, мы сможем выявить математические заблуждения студента и поработать с ними. Часто, однако, ответ студента даже не разумен. Тогда что мы делаем?

Этот сценарий заставил меня задуматься об Общем базовом стандарте математической практики 1:

Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение.

Лучший найденный мной способ помочь учащимся разобраться в проблеме — это, по иронии судьбы, вообще убрать вопрос. Вдохновленный замечательными людьми на Математическом форуме, я часто замечаю и удивляюсь таким образом учащимся. Совсем недавно, прочитав потрясающую запись в блоге Брайана Бушарта, я тоже начал выводить цифры! Вместо того чтобы во время чтения студенты думали о том, как они собираются решить задачу, они действительно думают о сложившейся ситуации. Это был замечательный способ дать каждому учащемуся доступ к проблеме и позволить мне выделить всех учащихся в классе. В то же время я получил представление о математическом понимании моих студентов.

Недавно мне довелось поработать с 3-классником. Они только что закончили работу над умножением и делением и вскоре приступили к работе над дробями. Чтобы их учитель и я могли видеть и слышать, как учащиеся применяют операции, понимают контекст и в настоящее время думают о дробях, я подумал, что было бы интересно взять сюжетную задачу из их рабочей тетради и вынуть вопрос и числа.

Планирование

Я выбрал приведенную ниже задачу и подумал о том, что я узнаю о математических знаниях и осмыслении учащихся после того, как они ответят на вопросы.

Основываясь на идее убрать числа и вопрос, я изменил задачу на это простое утверждение:

«У Вебстера есть коробки с батончиками мюсли, которыми он может поделиться со своим классом».

Я ожидал, что ученики будут недоумевать по поводу недостающих математических частей, связанных с открытым утверждением, подобным этому. Я полагал, что их любопытство может привести к возникновению вопросов, на которые можно было бы ответить, основываясь на той самой информации, которая их интересовала. Я знал, что математические идеи умножения, деления и/или дробного деления возникнут, и что я узнаю гораздо больше об их мышлении, чем если бы я дал им исходную задачу.

В классе

Я начал урок, повесив предложение на доске и записав то, что они заметили и удивились.

Они заметили:

«Мы не знаем, сколько там коробок с мюсли.»
«Недостаточно информации, чтобы понять, что происходит.»
«Мы не знаем, является ли это сложением, вычитанием, умножением или делением.»
«В классе несколько человек, потому что там написано ящики и поделись.»

Они задавались вопросом:

«Сколько батончиков мюсли в каждой коробке?»
«Сколько коробок он принес на урок?»
«Сколько детей в его классе?»
«Что это за батончики мюсли?»

Основываясь на том, что они заметили и о чем задавались вопросом, я чувствовал, что все хорошо понимают контекст и понимают, к чему все идет. Я понял, что «недостаточно информации, чтобы понять, что происходит», и спросил, что еще они хотели бы знать. Они ответили, что им нужны ответы на первые три вопроса: плитки на коробку, количество коробок и количество детей в классе.

Я спросил их, на какие вопросы они могли бы ответить, если бы я дал им эту информацию, и они ответили:

«Сколько у него слитков?»
«Сколько батончиков получает каждый ребенок?»
«Сколько у него осталось?»

В этот момент я мог бы дать им информацию, которую они хотели. Однако я подумал, что было бы гораздо круче позволить им самим выбирать эту информацию. Мне было любопытно, как они будут выбирать свои номера! Будут ли они разрабатывать стратегии в отношении чисел, чтобы облегчить себе задачу? Задумались ли они так далеко вперед? Что бы они сделали с остатками?

Когда я сказал им, что не даю им информацию, а вместо этого они выбирают свои собственные номера вместе с вопросом, на который хотят ответить, они были так взволнованы!

Некоторые партнеры очень тщательно выбирают свои номера, чтобы облегчить себе задачу. Для меня это продемонстрировало большую осмысленность и предусмотрительность того, что должно было произойти на их пути решения. И, в качестве дополнительного бонуса, несмотря на то, что группу попросили ответить только на один вопрос, группа ответила на все три! (Примечание для учителя: если учащиеся выбирают числа со стратегической точки зрения и поэтому заканчивают быстро, дайте им дополнительные штрихи, чтобы учесть их задачу и посмотреть, как они справятся с остатками.)

Другие студенты выбрали противоположный маршрут и стратегически выбрали номера, чтобы сделать его «сложнее для себя». Посмотрите, как эти два студента проявили твердую аргументацию и настойчивость при делении больших чисел, чем те, с которыми они когда-либо работали.

Другие выбрали номера без особых раздумий и разобрались с удивительными остатками. Это был отличный способ формативно оценить мышление учащихся, связанное с дробями, до того, как они приступили к этому разделу.

А потом всегда есть сюрпризы. Кто бы мог подумать, что третьеклассники будут рассуждать об остатках в процентах?

Выяснение того, что они знают

Размышляя о разнице между тем, что учащиеся сделали бы с исходной задачей, и работой по рассуждению, связанной с одним простым предложением, я поражен результатами. Я узнал намного больше о том, что знает каждый из учеников, помимо простого умножения пяти и шести. Удаление чисел и вопроса позволило каждому учащемуся подумать о значении предложения, подразумеваемых математических связях и спланировать путь решения, прежде чем приступать к попытке решения.

Я настоятельно рекомендую всем попробовать эту стратегию со словесной задачей из вашего текущего текста. Это прекрасный способ дать каждому учащемуся доступ к математике и свободу мысли, помимо простого получения ответа.

Если вы знаете меня или когда-либо читали мой блог, вы знаете, что я могу целыми днями говорить о школьных математических работах! Вы можете посетить мой блог для более подробного описания работы, показанной в этом посте, а также дополнительной работы, взятой из урока.