Содержание
Как объяснить ребёнку тему «Скорость. Время. Расстояние»
По статистике образовательной платформы iSmart, решение задач на движение входит в топ-10 самых сложных тем по математике для учеников начальной школы. Трудности возникают во взаимосвязях основных понятий и с путаницей в формулах. Давайте разбираться вместе.
С первых шагов человек преодолевает расстояние: от кроватки до игрушки, от дома до школы, от одного города до другого, от Земли до Луны.
Расстояние – это длина от одного пункта до другого, промежуток между чем-либо.
Например: расстояние от Москвы до Сочи 1361 км, от дома до детской площадки – 100 м.
Расстояние измеряется в шагах, в метрах, в километрах и т. д. То есть при измерении расстояния используют меры длины.
Расстояние можно измерить с помощью: линейки, измерительной ленты, рулетки, шагомера и т.п.
Расстояние обозначается латинской буквой S.
Время
Все мы помним, как медленно тянется время урока, когда нам неинтересно. И как быстро оно пролетает, если это любимый урок.
И как быстро оно пролетает, если это любимый урок.
Что же такое время?
Время – это продолжительность каких-то действий, событий.
Например, можно доехать на машине до магазина за 10 минут, а пешком дойти за час.
Измерить время можно минутами, часами, сутками и т. д.
Время измеряют с помощью часов: электронных, механических, песочных, атомных.
Время движения обозначается латинской буквой t.
Скорость
Если ребёнок уже с детства мечтает научиться водить автомобиль, можно рассказать, что в будущем ему точно пригодится знание формулы скорости. Ну и правила дорожного движения не помешают.
Скорость – это расстояние, пройденное за определённое время.
Её можно сравнить и измерить.
В чём же измеряют скорость? В м/сек (метр в секунду), км/ч (километр в час) и т. д.
Приборы измерения скорости:
- Спидометр – прибор, измеряющий скорость движения в автомобиле, мотоцикле, самокате.

- Радар – прибор, определяющий превышение скорости движущегося объекта.
Например:
Опасность! Автомобиль движется с превышением скорости по трассе. На спидометре 200 км/ч. Радар инспектора дорожной полиции зафиксировал превышение скорости.
Скорость обозначают латинской буквой V.
Взаимосвязь расстояния, времени и скорости
Скорость, время и расстояние взаимосвязаны. Как их найти? Существуют формулы определения скорости, времени и расстояния.
А теперь повторим формулы и приступим к работе.
Формула определения расстояния
Чтобы найти расстояние (S), нужно умножить скорость (V) на время движения (t):
S = V × t
Например:
Мотоциклист ехал 4 часа со скоростью 80 км/ч. Какое расстояние он проехал?
Если известны скорость и время, можно найти расстояние. Чтобы найти расстояние нужно:
4 часа – t (время)
80 км/ч – V (скорость)
неизвестно S (расстояние)
S = v (80 км/ч) × t (4 часа) = 320 км
S= 320 км
Формула определения времени
Чтобы найти время (t), нужно разделить расстояние (S) на скорость (V):
t = S : V
Например:
Электросамокат проехал 20 км со скоростью 10 км/ч. Какое время он был в пути? Как найти время, зная скорость и расстояние?
Какое время он был в пути? Как найти время, зная скорость и расстояние?
Если известны расстояние и скорость, можно найти время.
20 км – S (расстояние)
10 км/ч – V (скорость)
неизвестно t (время)
t = S (20 км) : 10 (км/ч)= 2 часа
t = 2 часа
Формула определения скорости:
Чтобы найти скорость (V), нужно расстояние (S) разделить на время движения (t):
V = S : t
Например:
Мышка, убегая от кота, пробежала 12 метров до норки за 4 секунды. С какой скоростью она бежала? Как найти скорость?
Если известны расстояние и время, можно найти скорость.
12 м – S (расстояние)
4 сек. – t (время)
неизвестно V (скорость)
Чтобы найти скорость, нужно:
V = S (12м) : t (4 сек.) = 3 м/сек.
V = 3 м/сек.
Чтобы ребёнку легче было запомнить условные обозначения, предложите вариант в стихотворной форме.
Хоть до дома, хоть до небес
Расстояние – это буква S.
И в Париже, и в Москве
Скорость – это буква V.
Точно скажем, без сомнения,
Буква t – это время движения.
5 полезных советов для родителей
А ещё постарайтесь следовать простым советам, которые здорово помогут вам сократить время выполнения домашней работы.
1. Не начинайте заниматься с ребёнком, если он голоден, устал, не хочет погружаться в тему или его что-то тревожит. Обязательно настройтесь на позитив.
2. Не ругайте ребёнка, если что-то не получается. Это нормально.
3. Хвалите его и радуйтесь даже незначительным успехам. Это очень важно для ребёнка.
4. Не начинайте новое задание, если не разобрались с предыдущим.
5. Используйте современные онлайн-платформы.
Если хотите, чтобы ваш ребёнок отточил навык решения задач на движение и добился хороших результатов, предложите ему выполнить задания на о iSmart. Здесь собрано около тысячи примеров на эту тему. Занимаясь 15 минут в день, ваш школьник самостоятельно:
Занимаясь 15 минут в день, ваш школьник самостоятельно:
- устранит пробелы в знаниях;
- доведёт до автоматизма вычислительные навыки;
- не будет бояться проверочных работ;
- повысит успеваемость на 1-2 балла.
Регистрируйте ребёнка на платформе iSmart и начинайте заниматься.
Лёгких вам совместных решений даже самых сложных задач!
Урок математики по теме «Скорость. Время. Расстояние». 4-й класс
Цели:
- закрепить знания нахождения скорости, времени,
расстояния; - ввести формулы;
- учиться решать задачи с этими величинами по
формулам и без них; - развивать мышление и память;
- прививать любовь к математике.
Ход урока
1. Организация учащихся.
2. Сообщение темы.
— Сегодня на уроке мы закрепим знания
нахождения скорости, времени, расстояния. Будем
Будем
учиться решать задачи с помощью формул.
— А работать мы будем в форме соревнований трех
команд:
- 1 ряд — автомобилисты
- 2 ряд — летчики
- 3 ряд — мотоциклисты
— Баллы будем выставлять на доске
3. Соотнести записи с картинкой.
— Как вы думаете, что написано на доске?
(Скорости)
— Соотнесите их с нужной картинкой.
(12 км/ч, 60 км/ч, 5 км/ч, 70 км/ч, 120 км/ч, 800 км/ч, 8 км/с, 50
км/ч,250 км/ч.
Автобус, самолет, ракета, пешеход, поезд,
велосипедист , автомобиль, пароход, мотоциклист)
Каждая команда выставляет по 3 ученика.
— Как вы понимаете км/сек, км/ч, м/мин.
Решение задач.
а) В тетрадь записываете ответ с наименованием.
Таблица на интерактивной доске.
| Скорость V | Время t | Расстояние S |
| 5 м/с | 15 сек. | ? м. |
Муха летела со скоростью 5 м/сек. 15 сек. Какое
расстояние она пролетела?
— Что известно?
— Повторите вопрос задачи.
— Как найти расстояние?
— Кто может записать буквами это правило?
— Запишите эту формулу в тетрадь s=v * t.
| Скорость V | Время t | Расстояние S |
| ? м/с | 3 сек. | 78 м. |
За 3 сек. Сокол пролетел 78 метров. Какова
скорость сокола?
— Что известно?
— Повторите вопрос задачи.
— Как найти скорость?
— Кто может записать буквами это правило?
— Запишите эту формулу в тетрадь v=s:t.
| Скорость V | Время t | Расстояние S |
| 10 м./сек | ? сек. | 100 м. |
Грач пролетел 100 метров со скоростью 10 м/сек.
Сколько времени он был в пути?
— Что известно?
— Повторите вопрос задачи.
— Как найти время?
— Кто может записать буквами это правило?
— Запишите эту формулу в тетрадь t=s:v.
Баллы. Молодцы!
б) Составление задач.
- 1 ряд — нахождение V
- 2 ряд — нахождение t
- 3 ряд — нахождение S
Баллы. Отлично.
в) Заполнить таблицу.
| Скорость V | Время t | Расстояние S |
| 90 км/ч | 6 ч. | ? км. |
| ? км/ч | 30 ч. | 1500 км |
| 70 м/мин. | ? мин. | 840 м |
Решение записываете в тетрадь с наименованием,
рядом записываете формулу.
Самостоятельная работа.
Проверка.
90 * 6 = 540 (км)
s=v*t
1500:30=50 (км/ч) v=s:t
840:70=12 (ч) t=s:v
Замечательно!
4. Работа с учебником.
Коллективное решение задачи стр. 60 №4
Две бабы-яги поспорили, что быстроходнее ступа
или помело? Одну и ту же дистанцию в 228 км баба-яга
в ступе пролетела за 4 ч, а баба яга на помеле за 3
ч. Что больше, скорость ступы или помела?
а) составление таблицы.
| Скорость V | Время t | Расстояние S | |
| ступа | |||
| помело |
б) решение у доски и в тетрадях.
1) 288:4=72 (км/ч) — скорость ступы
2) 288:3=96 (км/ч) — скорость помела
3) 96-72=24 (км/ч) — больше скорость помела, чем
скорость ступы.
Ответ запишите самостоятельно.
Баллы.
5. Физминутка.
6. Задача повышенной сложности.
Это очень интересно (на доске написана задача)
— Кто видел счетчик в автомобиле, который ведет
отчет километров, которые проехал автомобиль?
— Как он называется (спидометр).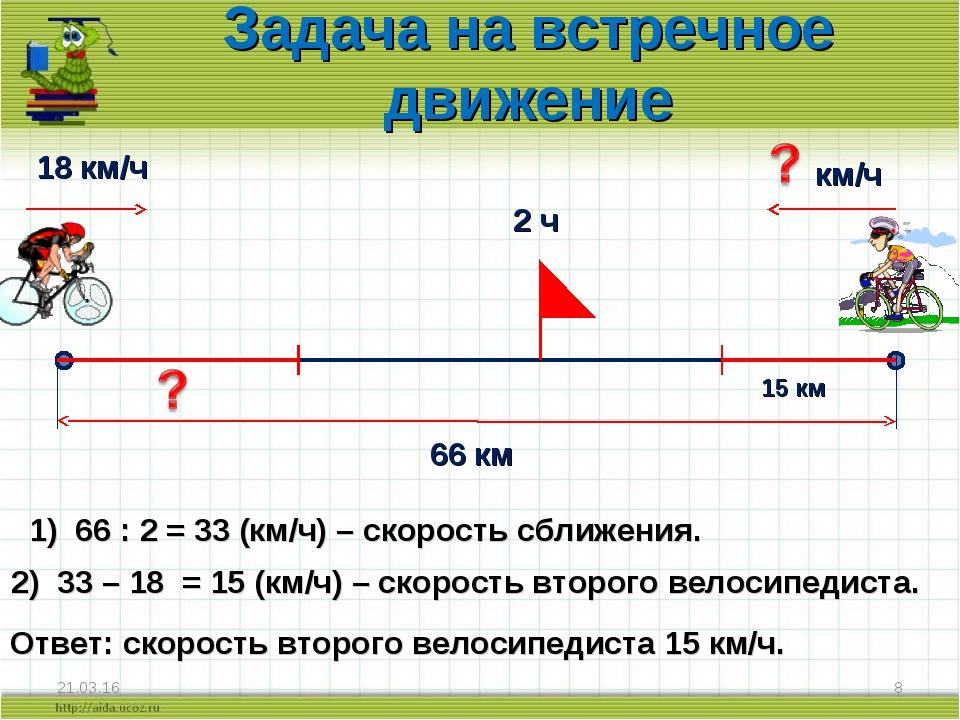
Счетчик автомобиля показал 12921 км. Через 2 час на
счетчике опять появилось число, которое читалось
одинаково в обоих направлениях. С какой
скоростью ехал автомобиль?
Решение.
1) 13031 — 12921=110 (км) — проехал за 2 ч.
2) 110 :2 = 55 (км/ч) — скорость автомобиля.
Ответ.
7. Итоги урока.
— Как найти расстояние, скорость, время
(формула).
— Баллы. Итог.
Молодцы! Всем огромное спасибо!
Дополнительная задача.
Туристы ехали в первый день 5 ч. На лодке со
скоростью 12 км/ч. Во второй день они были в пути
столько же времени, увеличив скорость на 3 км/ч.
Сколько километров проехали туристы на лодке во
второй день?
Самостоятельно заполнить таблицу и решить
задачу.
5 простых и полезных ресурсов для обучения скорости, расстоянию и времени ~ Мастер Сюань
9 февраля 2022 г. 27 декабря 2021 г.
В этой статье я поделюсь с вами 4 полезными ресурсами, которые легко использовать при обучении скорости, дистанции, времени. Так что не беспокойтесь больше о нехватке ресурсов для этой темы!
Так что не беспокойтесь больше о нехватке ресурсов для этой темы!
Вам нужны упражнения для запоминания формулы средней скорости?
Или вам нужна более серьезная практика, такая как словесные задачи на скорость?
Беспокоитесь о том, что вас будут считать скучным учителем при обучении этим понятиям?
Эти 4 ресурса без предварительной подготовки идеально подходят для вас!
Этот ресурс поможет познакомить ваших учащихся с использованием формул скорости, расстояния, времени для вычисления любой 1 переменной по двум другим значениям. Учащимся необходимо заполнить пропуски правильным ответом.
Это занятие доступно в 3 разных версиях: Boom™ Cards, Printable и Easel Activity. Это дает вам 3 различных способа использования этого действия. В каждом упражнении 25 вопросов.
Есть 30 карт стрел, которые позволяют учащимся вычислять скорость, расстояние и время.
Колода с несколькими вариантами ответов отлично подходит для просмотра всего класса с помощью интерактивной доски или для самостоятельной практики на устройствах учащихся. С изображением разных видов транспорта на каждой карточке это добавляет интереса к упражнениям.
С изображением разных видов транспорта на каждой карточке это добавляет интереса к упражнениям.
Содержимое:
- Расчет скорости по расстоянию и времени x10
- Нахождение расстояния, заданной скорости и времени x10
- Нахождение времени, заданного расстояния и скорости x10
Вы можете использовать это для математических центров и обзоров или давать в качестве домашнего задания.
Примечание. Доступно только на платформе Boom™ Learning.
После того, как вы научились вычислять скорость по расстоянию, времени и так далее, пришло время повеселиться! Вы всегда можете использовать это, чтобы мотивировать студентов быть более сосредоточенными при изучении формулы средней скорости. Пусть ваши ученики весело проведут время, и им обязательно понравится ваш урок!
Этот ресурс включает в себя 8 игр без подготовки, которые заинтересуют ваших учеников. Единицы, используемые во всем ресурсе, это км, ч и км/ч.
Содержимое:
- Пирамида Скорости – Найди линию (Расчет скорости, расстояния, времени) [Групповая игра]
- Соедини четыре (Расчет скорости, расстояния, времени) [Групповая игра]
- Доберись до дома ( Расчет скорости, расстояния, времени) [Групповая игра]
- Кто путешествовал больше всех? (Расчет расстояния) [Групповая игра]
- A) Путешествие на пляж (Расчет скорости по расстоянию и времени) [Лабиринт]
- B) Путешествие в горы (Расчет расстояния) [Лабиринт]
- C) Путешествие на остров (Расчет времени) [Лабиринт]
- Поездка по городу (Расчет скорости, расстояния, времени) [Сетка лабиринта]
- Ответы
Эта печатная форма имеет цифровую версию: Мольберт ТПТ. Так что вы все еще можете играть в них даже при дистанционном обучении. Кроме того, они отлично подходят для математических центров, начинающих или звонарей, досрочных занятий.
Так что вы все еще можете играть в них даже при дистанционном обучении. Кроме того, они отлично подходят для математических центров, начинающих или звонарей, досрочных занятий.
Вы можете использовать это для обучения задачам на скорость, чтобы учащиеся научились решать задачи на скорость. Это важно, поскольку словесные задачи, связанные со скоростью, часто связаны с реальными приложениями.
Это строгое задание доступно в 3 различных версиях: Boom™ Cards, Printable и Easel Activity. В каждом упражнении есть 20 вопросов на скорость, расстояние, время, словесные задачи.
СОДЕРЖАНИЕ:
- Примечания x3
- Словесные задачи на скорость расстояние и время x20
- Найдите расстояние, время и скорость, зная две другие переменные.
- Соотношение скоростей
- Догон
- Встреча
- Измерения: км/ч, м/с, м/мин
Хорошо, это не отдельный ресурс, а набор из 4 вышеупомянутых ресурсов. Итак, если вы заинтересованы во всех этих ресурсах, приобретите экономичный комплект «Расчет скорости, расстояния и времени » со скидкой 20%!
Итак, если вы заинтересованы во всех этих ресурсах, приобретите экономичный комплект «Расчет скорости, расстояния и времени » со скидкой 20%!
Преимущество цифровых ресурсов в том, что вы можете использовать их снова и снова. Стоимость на одного студента значительно снижается, если вы используете их с большим количеством студентов на протяжении многих лет.
Кроме того, если я добавлю больше ресурсов в будущем, вы сможете получить их бесплатно! Купите его и дайте мне знать, что еще вам нужно. Если моим ученикам это тоже понадобится, я не против создать его и добавить в комплект.
Заключение
Я создал 4 ресурса, чтобы у моих учеников была дополнительная практика. Я объединил его, создав 5-й ресурс, чтобы коллеги-учителя могли получить больше с меньшими затратами. Эти продукты полезны и просты в использовании в классе. Надеюсь, вы извлечете из них пользу.
Вы можете купить указанные ресурсы просто перейдя по ссылке. Или вы можете поискать более полезные математические ресурсы для учащихся в возрасте от 7 до 12 лет в моем магазине TPT или Boom Store.
Полезный пост: 3 лучшие стратегии преподавания математики в небольших группах или классах
Вот несколько булавок, которые вы можете сохранить, чтобы добавить этот пост в закладки. Сохраните их на своей доске Pinterest прямо сейчас! ↓
Задачи на скорость, расстояние и время: формулы, модуль
- Автор
ШВЕТА Б.Р. - Последнее изменение 28-11-2022
Когда дети или обычные люди применяют математику для решения задач из реальной жизни, основанных на скорости, времени и расстоянии , они узнают, что математика — это больше, чем задача, которую должен выполнить учитель. Это также дает детям жизненно важные навыки для влияния на свое окружение. Скорость движущегося объекта определяется как расстояние, которое он проходит за одну единицу времени. Эта статья расскажет нам о математической связи между скоростью, расстоянием и временем.
Хотя понятия скорости, времени и расстояния остаются прежними, типы вопросов, представленных в тестах, могут различаться. Одними из наиболее распространенных тем количественных способностей, которые задают в государственных тестах, являются скорость, время и расстояние. Это одна из тех тем, о которых студенты уже знают до того, как начнут готовиться к конкурсным экзаменам.
Одними из наиболее распространенных тем количественных способностей, которые задают в государственных тестах, являются скорость, время и расстояние. Это одна из тех тем, о которых студенты уже знают до того, как начнут готовиться к конкурсным экзаменам.
Учащимся необходимо изучить концепцию скорости, времени и расстояния. При регулярном выполнении задач они могут развить скорость, что, в свою очередь, поможет им получить более высокие оценки на экзамене. Продолжайте читать, чтобы узнать больше.
Скорость слова означает, насколько быстро что-то или кто-то движется. Если мы знаем пройденное расстояние и время, затраченное на это, мы можем оценить среднюю скорость объекта. Скорость, с которой движется объект, называется скоростью (прохождением определенного расстояния). Это скалярная величина, потому что она определяет только величину, а не направление.
Формула, используемая для определения скорости, имеет следующий вид:
Метр в секунду \((\rm{м/с})\) является единицей измерения скорости в системе СИ.
Пример:
Из приведенного выше примера видно, что по мере увеличения скорости время уменьшается.
Выучить формулы для скорости Время Расстояние
Время
Время — это измеренная продолжительность, в течение которой происходит действие или событие. Формула времени вычисляет, сколько времени требуется объекту, чтобы пройти определенное расстояние с заданной скоростью.
Секунды — единица измерения времени в системе СИ \((\rm{s}).\)
Расстояние
Длина отрезка, соединяющего две точки, называется расстоянием. Расстояние — это протяженность или количество пространства между двумя объектами, точками, линиями и т. д.
Метр — единица измерения расстояния в системе СИ.
Отношение скорости, времени и расстояния
Теперь мы рассмотрим математическое соотношение между скоростью, расстоянием и временем. Скорость движущегося тела – это расстояние, которое оно проходит за единицу времени.
\({\text{Скорость = }}\frac{{{\text{расстояние}}}}{{{\text{время}}}}\)
Если расстояние указано в километрах, а время равно в часах, скорость в километрах в час.
Скорость равна \(\rm{м/сек}\), если расстояние измеряется в метрах, а время измеряется в секундах.
\({\rm{Расстояние}} = {\rm{скорость}} \times {\rm{время}}\)
Метр — единица измерения расстояния в системе СИ.
\({\text{Время = }}\frac{{{\text{расстояние}}}}{{{\text{скорость}}}}\)
Секунды — это единица измерения времени в системе СИ \(( \rm{s}).\)
Когда расстояние постоянно, скорость обратно пропорциональна времени. Когда \(D\) постоянна, \(S\) обратно пропорциональна \(T\).
Затраченное время будет находиться в соотношении \(n : m\), если скорости равны \(m : n.\)
Когда пройденное расстояние остается постоянным, скорость обратно пропорциональна требуемому времени. В результате с ростом скорости время уменьшается, и наоборот.
Формулы скорости, расстояния и времени
С помощью этих формул можно решить все фундаментальные задачи. Применяя приведенные формулы, следует следить за правильным использованием единиц измерения. Когда пройденное расстояние остается постоянным, скорость обратно пропорциональна требуемому времени. В результате с ростом скорости время уменьшается, и наоборот.
Применяя приведенные формулы, следует следить за правильным использованием единиц измерения. Когда пройденное расстояние остается постоянным, скорость обратно пропорциональна требуемому времени. В результате с ростом скорости время уменьшается, и наоборот.
Единицы скорости, расстояния и времени
Время : секунды \((\rm{s})\), минуты \((\rm{min})\), часы \((\rm{hr} )\)
Расстояние : метры \((\rm{м})\), километры \((\rm{км})\), мили, футы
Скорость : \({\rm{м/с}} ,\,{\rm{км/ч}}.\) Если расстояние в \({\rm{км}}\) и время в \({\rm{ч}}\), то \ ({\text{Скорость =}}\frac{{{\text{расстояние}}}}{{{\text{время}}}}\), а единицей измерения скорости будет \(\rm{км/ч). }.\)
Влияние скорости и времени на расстояние
Поймите, что любая скорость, которую мы выбираем, включает в себя и расстояние, и время. «Быстрее» может означать «дальше» (большее расстояние) или «быстрее» (меньшее расстояние) (меньше времени). Чтобы одновременно удвоить пройденное расстояние, нужно увеличить скорость. Когда скорость человека увеличивается, то расстояние, которое он преодолевает, сокращается вдвое. Расстояние не зависит от скорости. Это может повлиять на время, необходимое для преодоления определенного расстояния.
Чтобы одновременно удвоить пройденное расстояние, нужно увеличить скорость. Когда скорость человека увеличивается, то расстояние, которое он преодолевает, сокращается вдвое. Расстояние не зависит от скорости. Это может повлиять на время, необходимое для преодоления определенного расстояния.
Реальные задачи на скорость, время и расстояние
1. Мальчик идет со скоростью \(5\,\rm{км/ч}\). Сколько времени ему потребуется, чтобы пройти \(20\,\rm{км}\)?
Мы знаем, \({\text{Время = }}\frac{{{\text{расстояние}}}}{{{\text{скорость}}}}\)
Итак, время, необходимое для ходьбы \ ( = \frac {20}{5} = 4\,\rm{часы}\)
Итак, мальчик идет \(20\,\rm{км}\) за \(4\,\rm{часа} \).
2. Велосипедист проезжает \(14\,\rm{миль}\) за \(2\,\rm{час}\). Вычислите его скорость.
Мы знаем, \({\text{Скорость = }}\frac{{{\text{расстояние}}}}{{{\text{время}}}}\)
Следовательно, \({\text {Скорость}} = \frac{14}{2} = 7\,{\text{миль}}\,{\text{в}}\,{\text{час}}. \)
\)
Итак, скорость велосипедистов составляет \(7\,{\text{миль}}\,{\text{за}}\,{\text{час}}.\)
3. Велосипедист едет со скоростью \( 25\,\rm{км/час}\). Какое расстояние он проедет за \(50\,\rm{минут}\)?
Мы знаем, \({\rm{Расстояние}} = {\rm{скорость}} \times {\rm{время}}\)
Итак, расстояние, пройденное за \(50\) минут \(25 \ раз \frac{{50}}{{60}} = 20,83\,{\text{км}}\)
Итак, велосипедист проезжает \(20,83\,{\text{км}}.\)
Решенные примеры – задачи из жизни на основе скорости, времени и расстояния
Q.1. Автомобиль проезжает \(320\,\rm{км}\) за \(4\,\rm{час}.\) Какова его скорость в \(\rm{км/ч}\)?
Ответ: Мы знаем, что формула скорости определяется выражением \({\text{Скорость =}}\frac{{{\text{расстояние}}}}{{{\text{время}}}}\ )
\( \Rightarrow {\text{скорость}} = \frac{{320}}{4} = 80\,{\text{км/ч}}.\)
Следовательно, скорость, с которой движется автомобиль равно \(80\,{\text{км/ч}}. \)
\)
Q.2. При движении со скоростью \(45\,\rm{км/ч}\), сколько времени потребуется, чтобы проехать \(135\,\rm{км}\)?
Ответ: Дано, скорость \(= 45\,{\text{км/ч}}\), расстояние \(= 135\,{\text{км}}\)
Мы знаем соотношение между скорость расстояние и время, \({\text{скорость}} = \frac{{{\text{расстояние}}}}{{{\text{время}}}}\)
\( \Rightarrow 45\, {\text{км/ч}} = \frac{{135\,{\text{км}}}}{{{\text{время}}}}\)
\( \Rightarrow {\text{время}} = \frac{{135\,{\text{км}}}}{{45\,{\text{км/ч}}}}\)
\( = 3\,{\text{часы}}\)
Следовательно, необходимое время для прохождения \(135\,{\text{км}}\) равно \( 3\,{\text{часы} }.\)
Q.3. Грузовик ехал из города с начальной скоростью \(40\,\rm{км/ч}\). Скорость грузовика увеличивалась на \(3\,\rm{км/ч}\) в конце каждого часа. Найдите общее расстояние, пройденное грузовиком за первые \(5\,\rm{часов}\) путешествия.
Ответ: Общее расстояние, пройденное грузовиком за первые \(5\,\rm{часов}\)
\(= 40 + 43 + 46 + 49+ 52\)
\(= 230\,\rm{км}\)
Следовательно, \(230\,\rm{км}\) — это общее расстояние, пройденное грузовиком за первый \(5\,\ rm{часы}\) пути.
Q.4. Арун может пробежать расстояние \(120\,\rm{м}\) за \(20\,\rm{секунд}\). Найдите скорость Аруна в \(\rm{м/с}.\)
Ответ: Дано, время \(= 20\,\rm{секунд}\), расстояние \(= 120\ ,\rm{m}\), скорость \(=\)?
Мы знаем, \({\text{скорость =}}\frac{{{\text{расстояние}}}}{{{\text{время}}}}\)
\( \Rightarrow {\text{скорость}} = \frac{{120}}{{20}} = 60\,{\text{m}}/{\text{s}}\)
Следовательно, скорость Аруна равна \(60\,{\text{m}}/{\text{s}}.\)
Q.5: Движение со скоростью \(50\,\rm{ км/ч}\) , сколько времени потребуется, чтобы проехать \(80\,\rm{км}\) ?
Ответ: Дано, скорость \(= 50\,\rm{км/ч}\), расстояние \(= 80\,\rm{км}\)
Мы знаем соотношение между скоростью, расстоянием и временем \({\text{время =}}\frac{{{\text{расстояние}}}}{{{\text{скорость}}}}\)
\( \Rightarrow {\text{time}} = \frac {{80}}{{50}}\)
\( \Rightarrow {\text{time}} = \frac {{8}}{{5 }}\)
\( \Rightarrow {\text{время}} = 1,6\;\rm{часы}\)
\( \Rightarrow {\text{время}} = 1\,{\rm{час}} \,36\,{\rm{минуты}}\)
Следовательно, \(1\,{\rm{час}}\,36\,{\rm{минут}}\) потребуется для путешествия \ (80\,\rm{км}. \)
\)
Q.6. Если расстояние, пройденное поездом, равно \(405\,\rm{км}\) в \(4\,{\rm{часа}}\,30\,{\rm{минут}}\), чему равно его скорость?
Ответ: Дано, время \(= 4\,{\rm{час}}\,30\,{\rm{минут}} = 4,5\,{\rm{час}}\), расстояние \(= 500\,\rm{км}\),скорость \(=\)?
Мы знаем, \({\text{скорость}} = \frac{{{\text{расстояние}}}}{{{\text{время}}}}\)
\( \Rightarrow {\text{скорость }} = \frac{{405}}{{4,5}}\)
\( \Rightarrow {\text{скорость}} = 90\,{\text{км}}/{\text{ч}}\)
Следовательно, полученная скорость равна \(90\,{\text{км}}/{\text{ч}}.\)
Q.7. Выразите скорость \(90\,\rm{метров}\) в минуту в километрах в час.
Ответ: Дано, скорость \( = 90\,{\text{метров}}/{\text{минут}}\)
Мы знаем \(1\,{\text{метр}} = \frac{1}{{1000}}\;{\text{км}}\) и \(1\,{\text{минута}} = \frac{1}{{60}}{\text{ час}}\)
Следовательно, скорость \(= 90 \times \frac{{\frac{1}{{1000}}{\text{км}}}}{{\frac{1}{{60} }\;{\text{hr}}}}\)
\( \Rightarrow {\text{скорость}} = 90 \times \frac{{60}}{{1000}}\)
\( \Rightarrow { \text{скорость}} = 9 \times \frac{6}{{10}}\)
\( \Rightarrow {\text{скорость}} = \frac{{54}}{{10}}\)
\( \Rightarrow {\text{скорость}} = 5,4\,{\text{км}}/{\text{ч}}\)
Следовательно, скорость может быть выражена как \(5,4\,{\text {км}}/{\text{ч}}. \)
\)
Q.8. Автомобиль проезжает расстояние \(600\,{\text{км}}\) за \(10\,{\rm{часов}}\) . Какова его скорость?
Ответ: Дано, время \(= 10\,\rm{часов}\), расстояние \(= 600\,\rm{км}\), скорость \(=\)?
Мы знаем, что \({\text{скорость}} = \frac{{{\text{расстояние}}}}{{{\text{время}}}}\)
\(\Стрелка вправо {\text{скорость}} = \frac{{600}}{{10}}\)
\( \Стрелка вправо {\text{скорость}} = 60\,{\text{км}} /{\text{ч}}\)
Следовательно, полученная скорость равна \(60\,{\text{км}}/{\text{ч}}.\)
Резюме
Эта статья включает определение скорости, расстояния и времени, отношения между этими тремя формулами. Это помогает решать различные проблемы, в том числе проблемы из реальной жизни, слишком быстро. Эта статья поможет лучше понять «Реальные жизненные проблемы, основанные на скорости, времени и расстоянии». Результаты этой статьи помогают применять подходящие формулы при решении основанных на них различных задач.
Решение важных проблем в поездах
Часто задаваемые вопросы (FAQ)
Мы предоставили некоторые часто задаваемые вопросы здесь:
Q.1. Какова формула скорости и расстояния?
Ответ: Формула для определения скорости имеет вид \({\text{скорость}} = \frac{{{\text{расстояние}}}}{{{\text{время}} }}\)
Формула для определения расстояния имеет вид \({\text{расстояние}} = {\text{скорость}} \times {\text{время}}.\)
Q.2. В чем разница между скоростью и расстоянием?
Ответ: Скорость, с которой проходится расстояние в единицу времени, называется скоростью. Скорость равна \(S = \frac{D}{T}\), если ‘\(D\)’ — это расстояние, пройденное объектом за время ‘\(T\)’.
Q.3. Как скорость и время влияют на расстояние?
Ответ: Какую бы скорость мы ни выбрали, помните, что она включает в себя расстояние и время. Увеличение скорости предполагает увеличение пройденного пути за то же время. Увеличение скорости также сокращает время, необходимое для преодоления того же расстояния.
Увеличение скорости предполагает увеличение пройденного пути за то же время. Увеличение скорости также сокращает время, необходимое для преодоления того же расстояния.
Q.4. Как вы решаете задачи, связанные со скоростью, расстоянием и временем?
Ответ: Скорость рассчитывается по формуле \({\text{скорость}} = \frac{{{\text{расстояние}}}}{{{\text{время}}}}. \) Нам нужно знать единицы измерения расстояния и времени, чтобы вычислить единицы измерения скорости. Поскольку расстояние измеряется в метрах \((\rm{m})\), а время измеряется в секундах \((\rm{s})\), единицами измерения будут метры в секунду \((\rm{ м/с}).\)
В.5. Как найти скорость и расстояние в математической задаче?
Ответ: Скорость и расстояние можно рассчитать по формуле
\({\text{скорость}} = \frac{{{\text{расстояние}}}}{{{\text{ время}}}}\)
Формула для нахождения расстояния имеет вид В.
