Содержание
Деление в столбик ➗ примеры и правила, как научиться
Деление с остатком
Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:
Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме.
Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.
Деление трехзначного числа на однозначное
Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить;
- 7 — делитель или то, на что нужно поделить:
- частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Для этого рассмотрим первую цифру делимого. Она меньше делимого: 3 < 7 — не подходит.
Рассмотрим теперь две первые цифры делимого: 32 ﹥7. Подходит!
Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.
Важно
Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Деление трехзначного числа на двузначное с примерами
Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.
Пример №1.
Разделим трехзначное число 324 на двузначное 81.
Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.
Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!
Шаг 3. Записываем 4 в столбик под делителем.
Это и есть ответ.
Ответ: 324:81=4.
Пример №2.
Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.
Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.
Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.
Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.
Ответ: 368:92=4.
Как делить однозначные и многозначные числа в столбик с остатком
Как мы писали в начале, это такое же деление, только в результате получается неровное число.
Теперь разберем те же примеры, только поделим в столбик.
Пример №1
Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.
Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.
Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.
Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.
Ответ: 19:5=3
Пример №2.
Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.
Шаг 1.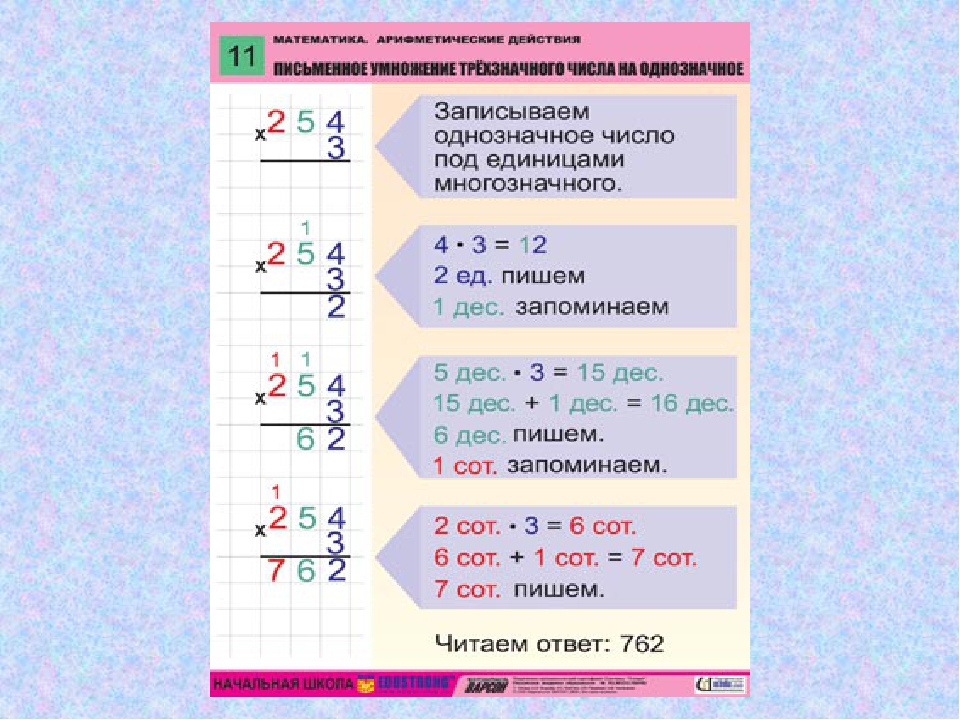
Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.
Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.
Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.
Ответ: 29:9=4(5)
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Примеры на деление в столбик для 3 класса
Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье.
Это задание со звездочкой.
Легкий уровень | Средний уровень | Сложный уровень |
27:3= 48:4= 56:8= 72:9= 95:5= | 270:15= 504:14= 315:5= 728:8= 855:9= | 1749:11= 1080:45= 3888:72= 5248:64= 4818:66= |
Ответы:
- легкий уровень: 9; 12; 7; 8; 19;
- средний уровень: 18; 36; 63; 91; 95;
- сложный уровень: 159; 24; 54; 82; 73.
Если вам интересно, как еще можно научить ребенка делить двузначные и трехзначные числа, приглашаем на вводный урок в Skysmart! На
на онлайн-курсах по математике для детей можно закрепить тему «Деление в столбик» и разобраться в других разделах из школьной программы.
4 простых способа научить ребенка делить столбиком — без слез и скандалов
Кажется, математика в начальной школе — это очень просто. Но есть темы, с которыми дети (и даже некоторые взрослые) не справляются. Одна из них — деление столбиком. Наш блогер, учитель начальных классов Ольга Катаева, рассказывает, как помочь ребенку освоить этот навык.
Одна из сложнейших тем по математике в начальной школе — деление столбиком. Поэтому материал в учебнике выстраивается от простого к сложному. Подготовка к делению столбиком начинается во втором классе. Основа — знание таблицы умножения, ведь деление — обратное умножению действие.
Что делать, если у ребёнка не получается делить столбиком? Для начала надо понять, в чем причина:
- знает ли ребенок таблицу умножения?
- умеет делить с остатком?
- умеет вычитать столбиком?
- понимает ли, что такое «метод подбора»?
- правильно ли оформляет запись (цифра под цифрой, единицы под единицами, десятки под десятками)?
- достаточно ли тренировался делить столбиком?
«Деление столбиком» нужно объяснять индивидуально: конечно, учитель в школе расскажет, но и родителям важно повторить дома еще раз, чтобы у ребенка была возможность задать вопросы.
Вот несколько советов родителям.
1. Замените математические термины на понятные ребёнку
Например, термин «первое неполное делимое» можно заменить на «деление по частям», «метод подбора» — сколько раз число помещается в неполном делимом — части.
2. Научите пользоваться таблицей умножения
Объясните, как пользоваться таблицей умножения при подборе числа
3. Разбирайте разные примеры
Есть разные случаи деления столбиком: деление на однозначное число, на двузначное, трёхзначное, деление чисел, в записи которых есть нули, деление чисел с нулями в конце, деление, когда в значении есть нули в середине и другие. Каждый отдельный случай лучше разбирать вместе с ребёнком (после объяснения учителем на уроке). Подобрать примеры на деление столбиком на каждый случай поможет учебник. Прорешивайте предыдущие номера.
Если примеров на деление столбиком мало в учебнике, составьте сами: перемножьте разные числа, поменяйте местами значение и один из множителей и запишите примеры на листочек.
4. Уточните с ребёнком понятия «число» и «цифра»
Давайте попробуем: разделим 2788 на 82. Начнём с оформления записи. Чтобы исключить ошибки в вычислениях, пишем по принципу «цифра под цифрой». Далее: первая часть — 2 (в разряде тысяч) — не подходит, 2 меньше 82. Следующая часть — 27 (сотен) — тоже не подходит, так как 27 меньше 82.
Тогда берём 278. При этом определяем сколько цифр будет в ответе. В данном примере — 2. Подбираем число: мысленно прикрываем последние цифры в делимом и делителе, получается, нужно поделить 27 на 8 — деление с остатком. В таблице умножения на 8 ищем близкий ответ — это 24, поэтому попробуем взять по 3. Умножаем 82 на 3, получается 246 — подходит.
Записываем 246 под первой частью — 278 — единицы под единицами, десятки под десятками, сотни под сотнями. Находим остаток, вычитанием (нужно уметь вычитать столбиком). Получается 32. 32 меньше 82, значит, первую цифру ответа подобрали правильно.
Осталась ещё часть — 8. Переносим 8 в строчку с остатком — 328.
Следим, чтобы в записи соблюдался принцип «цифра под цифрой». Подбираем цифру ответа. При подборе последней цифры ответа ориентируемся, в том числе, на последние цифры остатка и делителя — это 8 и 2. Прикрываем последние цифры остатка и делителя, получаем, что 32 нужно делить на 8. В таблице умножения на 8 находим число 4. Проверяем, подходит ли 4. Умножаем 82 на 4, получаем 328.
Записываем результат умножения под остатком, соблюдая принцип «цифра под цифрой», находим вычитанием остаток — это 0. Записываем 0. Деление выполнено. Результат (ответ) — 34.
Воспринимать инструкцию на слух очень сложно, особенно детям. Читать инструкцию тоже трудно — нужно вчитываться, вникать в смысл, следить, как связаны предыдущий и следующий шаги. Длинную инструкцию надо делить на смысловые части. Есть ученики, которым нужно «показать пальцем», куда какую цифру вписать, где какое число найти. Приём «покажи пальцем» отлично срабатывает при индивидуальном объяснении.
Не дожидайтесь, когда ребёнок перестанет справляться с вычислениями в теме «Деление столбиком», поддерживайте его и, главное, выучите таблицу умножения после окончания 1-го класса.
Практика показывает, что потом запомнить ее становится всё труднее и труднее.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Фото: k_samurkas / Shutterstock / Fotodom
Как помочь вашему ребенку выучить стратегии деления на деление и длинное деление – радость обучения
Когда моя дочь начала заниматься делением в четвертом классе, я знала, что у нас будут проблемы (и дополнительные занятия по математике дома). Как родителю, изучавшему математику «старым» способом, мне было очень трудно понять процессы, лежащие в основе ее домашних заданий по математике и текстовых задач. (Мне стыдно признаться, что задачи на разделение слов в четвертом классе — это не шутки.) Я использовал книгу Эван-Мура Math Fundamentals 9.0004, чтобы изучить, попрактиковаться и просмотреть стратегии подразделения. Визуальные модели и пояснения обеспечили пошаговый процесс обучения, который закрепил то, что моя дочь изучала в школе, и углубил ее понимание.
Помогая своей дочери освоить деление в длинное число, я даже обнаружил стратегии, лежащие в основе процесса деления, которые углубили мое понимание взаимосвязи между делением и умножением.
Деление — это один из тех математических навыков, которые заслуживают большого внимания, объяснений и практики. Сегодняшняя учебная программа по математике не учит математике как набору систем/этапов для запоминания, а включает в себя фундаментальные мыслительные процессы, лежащие в основе каждого навыка и стратегии, которым обучают детей. Сегодняшняя учебная программа по математике требует, чтобы дети понимали, почему они делают эти шаги, и использовали это понимание числовых отношений для более эффективного решения задач. Если дети знают, почему они делают определенные шаги, они могут применять это понимание для решения различных математических задач и понимать беглость чисел на более глубоком уровне.
Вот некоторые из стратегий и концепций, которые мы практиковали, и которые помогли мне и моей дочери лучше понять деление.
Начальные сведения о делении и умножении
По мере того, как ваш ребенок начинает изучать деление, ему/ей важно понимать взаимосвязь между делением и умножением. Дети должны хорошо знать факты умножения. (Если они не знают своих фактов об умножении, бегло потренируйтесь в течение нескольких недель, прежде чем начать деление.) Ознакомьтесь с дополнительными ссылками ниже, чтобы получить советы и идеи, чтобы узнать факты умножения.
Связь между умножением и делением
Начало деления учит простой концепции: чтобы делить, нужно умножать. Использование наглядных примеров умножения и деления поможет вашему ребенку научиться распознавать разницу между умножением и делением.
Если вы привыкли к старому методу деления, этот процесс может показаться утомительным, но детям важно понимать разницу между умножением и делением. Когда задачи с числами и словами становятся более сложными, это фундаментальное понимание поможет им понять, когда делить, а когда умножать.
Модель, как найти неизвестное число с помощью умножения или деления.
Чтобы узнать, понимает ли ваш ребенок основную взаимосвязь между умножением и делением, спросите его или ее:
Ответ: Факты об умножении и делении связаны. Если вы знаете один факт, вы можете решить другой связанный с ним факт.
Стратегии трех разделов
Один из аспектов текущего учебного плана по математике, который мне нравится, заключается в том, что он сосредоточен на обучении нескольким стратегиям и позволяет детям решать, какая из них лучше всего подходит для них. Этот подход позволяет детям понять и выбрать, какой метод наиболее подходит для их стиля обучения. Использование различных подходов иногда может даже привести к успеху или неудаче в математике. Вот три различных стратегии, которым следует учить, когда вы начинаете деление.
1. Установите связи с помощью шаблонов деления и разбейте числа
Это лучшее владение числами.
Обучение детей распознаванию и использованию шаблонов в числовых операциях сделает их очень эффективными в решении задач.
6000 ÷ 3
6 ÷ 3 = 2
6000 ÷ 3 = 2000
. Подумайте о 6000, разделенных на 3 тысячи, разделенных на 3, и это 2 тысячи.
2. Разбиение чисел на «дружественные» числа с использованием модели площади
260 ÷ 5 = 52
Разбить числа на «дружественные» числа. Разбивка чисел на легко делимые числа важна для беглости чисел. Это может показаться немного утомительным, но понимание того, как разбивать большие числа на числа, которыми легче манипулировать, может развить у детей математические способности в уме.
Разобьем 260 на «дружественные» числа 250 и 10. Я выбрал 250, потому что это делитель 5, умноженный на большое число (50). Я выбираю 10, потому что это разница между 250 и 260. Они входят в рамки модели области. Разделите каждое на делитель, чтобы получить множители, затем сложите множители вместе.
3. Разделить путем вычитания групп
623 ÷ 4
Я могу составить группы по 4 и вычитать их из 623 до тех пор, пока не останется достаточно, чтобы составить группу. Я начну со 100 групп по 4. Остается 223. Затем я вычту 50 групп по 4. Теперь у меня осталось 23. 5 групп по 4 человека израсходуют большую его часть; не осталось достаточно, чтобы вычесть даже 1 группу из 4. Наконец, я суммирую количество групп из 4 и запишу остаток.
Длинное деление: деление многозначных чисел с помощью моделей площадей, частичных частных и стандартного алгоритма
Если я только что потерял вас, используя такие фразы, как «частичные частные» и «стандартный алгоритм», не пугайтесь.
Это всего лишь математические термины для пошаговых процессов. Частное — это ответ, а частичное частное — это частичный ответ. Стандартный алгоритм — это пошаговый способ решения проблемы. Длинное деление использует эти стратегии для включения многократного вычитания, чтобы в конечном итоге найти ответ.
Деление многозначных чисел с использованием модели площади
Ранее мы занимались этим с началом деления, но теперь числа становятся больше и немного сложнее.
3,182 ÷ 15 = 212 R2
Деление — это просто повторное вычитание. Я создам группы по 15 и буду вычитать их до тех пор, пока не останется достаточно для вычитания. Затем я добавлю количество групп. Так как у меня получилось число меньше делителя, я запишу его как остаток.
3,182 ÷ 15 = 212 R2
Разделить с использованием неполных частных
Как и в модели площади, я найду группы делителя и вычту их. Потом сложу номера групп и напишу остаток, если он есть.
Разделить по стандартному алгоритму
Если вы вздохнете с облегчением на этом примере, то я вас полностью понимаю. Это традиционный способ обучения делению, который многие из нас усвоили много лет назад.
Этот стандартный алгоритм этого длинного деления повторяется с шагами:
1. Разделение
2. Умножьте
3. Вычтите
4. Сбросьте следующую цифру
5 4. , Повторите
* Многие дети путаются с шагами 2 и 3 , потому что на самом деле вы не делите, а умножаете и вычитаете, чтобы найти остаток.
3,182 ÷ 15 = 212 R2
Смотри только на одно место за раз, начиная слева. Поскольку 15 не делится на 3, я перехожу к следующему месту. Теперь прикидываю, сколько раз 15 войдет в 31 и пишу, что над 1. Вычитаю и сбиваю цифру со следующего места.
Я продолжаю делать это через дивиденд (число). Когда у меня закончатся места, я напишу оставшееся число как остаток.
Лучший способ помочь ребенку овладеть сложным навыком деления — практиковаться, практиковаться и еще раз практиковаться. Узнайте, какой метод лучше всего подходит для вашего ребенка, и дайте ему или ей множество практических задач для решения. Также не забывайте решать задачи на деление слов. Решение текстовых задач может продемонстрировать, насколько хорошо ваш ребенок понимает понятие деления и как его использовать.
Рекомендуемые ресурсы
Все примеры и стратегии были взяты из учебника Evan-Moor Math Fundamentals для 1–6 классов. Хотя это ресурс для занятий в классе, я обнаружил, что математические модели и практические задания легко использовать дома.
Для дополнительной практики решения текстовых задач просмотрите Daily Word Problems: Math Эван-Мура для 1–6 классов.
Советы по решению текстовых задач и умножению см.
в следующих статьях:
Хизер Фуди – сертифицированный учитель начальных классов с более чем 7-летним опытом работы педагогом и волонтером в классе. Ей нравится создавать уроки, которые являются значимыми и творческими для студентов. В настоящее время она работает в команде по маркетингу и коммуникациям Evan-Moor, и ей нравится создавать возможности для обучения, которые являются значимыми и творческими как для студентов, так и для преподавателей.
Категории: Стратегии работы в классе, Идеи для уроков |
Теги: математика 3-го класса, математика 4-го класса, дивизия 5-го класса, общее ядро дивизии, стратегии дивизии, дивизия четвертого класса, как преподавать дивизию, математика, дивизия третьего класса |
Постоянная ссылка
Как делать деление в длинное: простое пошаговое руководство с иллюстрациями
Вы провели свой класс через большинство больших единиц: сложение, деление, вычитание, умножение. Но вот еще одна хитрость:
Как выполнить деление в большую сторону.
Исследование 2012 года, опубликованное в Psychological Science, показало, что понимание пятиклассниками дробей и деления может быть напрямую связано с тем, насколько хорошо они понимают алгебру в старшей школе и успевают ли они на уроках математики более высокого уровня — даже после учета различных социально-экономических факторы. Никакого давления, верно? Если при мысли об обучении делению на длинные лады у вас холодный пот и липкие ладони, не беспокойтесь — мы сделали всю работу за вас.
Как выполнить деление в большую сторону за шесть шагов
1. Повторить
Первый шаг, который вы должны сделать, это шаг назад.
Для ученика 4-го класса деление в большую сторону представляет собой сложную смесь различных операций. Чтобы успешно научиться выполнять деление в большую сторону, им необходимо повторить эти фундаментальные понятия.
Согласно французскому исследованию, «представление и извлечение математических фактов из долговременной памяти» является одним из наиболее важных факторов, определяющих будущие математические успехи учащихся.
Согласно тому же исследованию, длинное деление — это «синтез всех арифметических знаний».
Убедитесь, что ваши ученики понимают, что умножение — это результат многократного сложения, а деление — просто противоположное — многократное вычитание.
Используйте блоки с основанием 10 или деньги, чтобы усилить значение места и чувство числа. Запланируйте занятия, в которых учащимся будет предложено создать «семейство фактов», чтобы убедиться, что учащиеся понимают, как взаимодействуют различные функции.
Используйте игры на умножение и другие математические игры, чтобы заинтересовать учащихся в учебе и развить уверенность в математике, прежде чем продолжить.
2. Начните с простого
Давайте начнем с урока словарного запаса. Уравнение деления на деление состоит из множества частей. Убедитесь, что ваши ученики знают, что они имеют в виду и как их идентифицировать.
Дивиденд — это число в правой части уравнения под чертой.
Он представляет собой сумму, которую нужно разделить.
Делитель — это число слева — оно выполняет деление.
Частное — это число сверху. Он представляет собой ответ или количество единиц в каждом разряде после завершения уравнения.
Остаток — это число вверху справа. Он представляет оставшиеся единицы, которые не могут быть равномерно разделены на частное. Во-первых, введите уравнение, которое не имеет остатков, чтобы учащиеся могли привыкнуть к формату и начать понимать новый словарный запас, который они только что изучили:
Спросите учащихся, сколько раз 2 умещается в 4. Это может показаться им сложной концепцией, поэтому используйте идею обмена: если вы хотите разделить 4 предмета между двумя людьми, сколько предметов получит каждый?
Как только они придут к правильному ответу, поставьте 2 выше 4. Затем повторите шаг со второй цифрой в делимом.
Используйте эти простые уравнения, чтобы усилить позиционное значение.
Объясните учащимся, что, когда они спрашивают, сколько раз 2 может превратиться в 4, на самом деле они спрашивают, сколько раз 2 превращается в 40. они удобны с основным форматом. Тогда пришло время двигаться дальше.
Вместо того, чтобы сразу перейти к уравнению с остатками, начните с другого предметного урока . Разделите учащихся на группы по три, четыре или шесть человек и дайте каждой группе по 50 ватных шариков (или мармеладок, или помпонов, или зефира — любой маленький предмет, доступный в вашем классе).
Попросите учащихся разделить предметы так, чтобы у каждого члена группы было одинаковое количество предметов, а затем наблюдайте и ждите.
В конце концов, они поймут, что не могут разделить его поровну, и всегда будут оставаться какие-то предметы. Вот где вы приходите, чтобы спасти положение и объяснить, как выполнить деление в большую сторону с помощью 9.0011 осталось .
Сначала покажите учащимся задачу с остатком в единицах:
Теперь начните со столбца десятков и проработайте задачу: 5 входит в 5 ровно один раз, так что там ничего не осталось.
Но сколько раз 5 входит в 7, и что вы делаете с остатками?
Покажите учащимся новые шаги:
- Разделить столбец единиц делим на делитель
- Умножить делитель на частное в нужном месте столбец
- Вычтите произведение из столбца единиц
Оставшееся число — это остаток. Обязательно смоделируйте несколько задач всем классом, чтобы учащиеся могли начать понимать этапы и то, как правильно записывать свои ответы.
Это хорошее время на уроке, чтобы научить учащихся проверять свои ответы. Пусть они умножат делитель на частное и прибавят остаток — ответ должен быть таким же, как и делимое, с которого они начали.
4. Остаток в десятках
Теперь пришло время учащимся решить задачи, в которых делитель не вписывается в столбец десятков или единиц. Шаги почти такие же, за исключением одного нового дополнения:
- Разделить делимое в столбце десятков на делитель
- Умножить делитель на частное в столбце десятков
- Вычесть произведение из делителя
- Сократите делимое в столбце единиц и повторить .
Для простоты начните с однозначных делителей и двузначных дивидендов. Помните, что это совершенно новая концепция для учащихся, поэтому найдите время, чтобы смоделировать задачи на доске. Обсудите, почему эти шаги работают, и помогите им понять, какую важную роль в этом процессе играет значение места.
5. Постепенно вводите большие числа
Вот и все. Или это?
Пусть учащиеся освоятся с формулой и поработают над более мелкими задачами. Когда они обретут уверенность и начнут понимать, как выполнять деление в большую сторону, начните предлагать им задачи с трехзначным делимым, а затем задачи с двузначным делителем.
Напомните учащимся, что шаги остаются одинаковыми, независимо от того, насколько велика задача , и предложите им использовать лист бумаги, чтобы «угадать и проверить» свое умножение по ходу дела. Это хороший момент, чтобы убедиться, что у них нет проблем и что они полностью понимают взаимосвязь деления с разрядным значением и умножением.
Посмотрите это видео от Khan Academy:
0012 Если вы рассмотрели весь свой контент на первых пяти шагах, поздравляем! Предложите учащимся продолжать практиковаться в делении больших и малых чисел в длинную и укреплять связь между делением и другими математическими понятиями, которые они изучают. Но процесс еще не завершен — учащиеся должны понять, как делать длинную деление с десятичной дробью. Для начала вернемся к одному из фундаментальных понятий деления: разрядному значению. Однако на этот раз вы будете двигаться назад, а не вперед. Предложите учащимся решить задачу, как обычно. Когда они дойдут до шага, на котором они обычно останавливаются с остатком, попросите их поставить десятичную точку в конце частного и делимого и написать несколько нулей после делимого. Предложите им продолжить обычные шаги деления на один или два знака, опуская нули. Соедините десятичную дробь с дробью. Попросите их преобразовать частное с десятичной дробью в неправильную дробь. Как выполнить деление в длинное число (без деления в длинное число) Поздравляем! Ваш модуль подходит к концу, и вы успешно научили своих учеников выполнять деление в большую сторону. Но знаете ли вы, что существует несколько способов деления больших чисел? Обучение учащихся другим способам проверки своей работы является важной частью математических стандартов Common Core и может улучшить понимание учащимися того, что на самом деле означает деление в столбцах в данном контексте. Плоскостные модели Плоскостные модели — отличный способ для визуалов понять и осмыслить деление, а также улучшить чувство числа. Этот метод использует сетку, чтобы представить процесс деления как задачу площади: например, 148÷4 можно разделить на сетку высотой 4 единицы, площадью 148 квадратных единиц и шириной неизвестного числа единиц. Учащиеся разбивают сетку на более удобные области: 100 квадратных единиц, 40 квадратных единиц и 8 квадратных единиц. 100÷4 равно 25, 40÷4 равно 10, а 8÷4 равно 2. Эти числа идут вверху модели области и могут быть сложены, чтобы получить ответ. Частичное частное Подобно модели области, частичное частное побуждает учащихся разбивать вопросы на деление на «более понятные» части. Это помогает учащимся понять, что деление — это нахождение того, сколько раз одно число может перейти в другое число. Задайте задачу (в данном случае 450÷23) как уравнение деления на деление. Попросите учащихся умножить делитель на 2 и 5, чтобы использовать его в качестве удобного ориентира. Спросите, сколько раз 23 входит в число 400, но не ищите точное ближайшее число: сделайте его удобным для работы, например, 230 (десять раз). Вычтите 230 из 450 и поставьте 10 справа, чтобы отслеживать результат. Возьмите разницу и вычтите ее из делимого. Спросите, сколько раз 23 входит в 220. 5 x 23 равно 115, так что вычтите это из 220 и запишите 5. Продолжайте, умножая и вычитая, пока окончательное число не станет слишком маленьким. Когда вы достигли этого шага, вы нашли остаток! Сложите числа в правом столбце, чтобы найти частное. Частичные частные обладают гибкостью, которой нет в длинном делении. Длинное деление нужно делать точно, но с частичными частными можно просто несколько раз вычесть делитель из делимого и все равно прийти к правильному ответу. Используйте этот метод, чтобы закрепить позиционное значение и концепцию деления как многократного вычитания. Упражнения на деление в длинное число Лучший способ научиться делению в длинное число – это практиковаться, практиковаться и еще раз практиковаться. Вот список из восьми заданий, которые заинтересуют ваш класс делением в длинную и помогут развить прочные математические навыки. 1. Prodigy Prodigy — это увлекательный и увлекательный ресурс для занятий в классе или дома на длинные дистанции. Учащиеся исследуют мир, полный приключений, где успех зависит от правильных ответов на математические вопросы. С помощью панели управления учителя вы можете предоставлять контент, ориентированный на урок, в зависимости от оценки, навыков или ученика. Затем учащиеся отвечают на эти вопросы в игре и предоставляют вам обратную связь в режиме реального времени о своем обучении и понимании . Поощряйте своих учеников практиковать все математические навыки, которые они изучили в классе, включая деление в столбик. Вот как вы можете использовать Prodigy для: Учащиеся играют в увлекательную игровую платформу, где они могут собирать питомцев, выполнять квесты и сражаться с друзьями. Зарегистрируйтесь сейчас 2. Деление в натуральную величину Оживите математику с помощью практической головоломки с делением в натуральную величину. Вырежьте квадраты из цветной бумаги со всеми числами, которые нужны учащимся для решения задачи на деление в длину от начала до конца. Используйте клейкую ленту, чтобы разделить линии на полу, и раздайте учащимся пронумерованные карточки. Попросите учащихся, начиная с заданного уравнения, разложить все карточки в правильном порядке, чтобы решить уравнение. Это задание побуждает учащихся замедлиться и подумать о своих шагах, и это особенно полезно для класса, который все еще хочет освоить шаги умножения. 3. Бинго с длинными дивизионами Бинго является классикой не просто так. Каждая из цифр в листе учащегося должна соответствовать вопросу, который вы задали перед классом. Бросьте вызов своим учащимся, но убедитесь, что вы уделяете этому упражнению достаточно времени — некоторые учащиеся могут испытывать трудности с быстрым решением задач и могут расстраиваться или совершать ошибки, если не смогут справиться с заданием. 4. Книги по математике Повысьте уровень грамотности и обучения математике с помощью забавных книг, посвященных сложным математическим понятиям. Используйте их, чтобы объяснить учащимся деление и остатки в веселой и увлекательной форме и даже охватить более основные понятия, прежде чем они начнут учиться выполнять деление в столбик. Некоторые книги по математике, которые охватывают дивизион, включают: Длинное деление состоит из множества шагов, и их нужно выполнять в правильном порядке, чтобы получить правильный ответ. Учащиеся могут запутаться или расстроиться, если не помнят шагов, что отрицательно сказывается на их уверенности в математике и успеваемости. Предложите учащимся придумать свой собственный уникальный способ запомнить, как выполнять деление в большую сторону — разделить на , умножить , вычесть и записать — чтобы стимулировать творчество в вашем классе. Предложите им создать постер, песню, мнемоническое устройство или даже небольшую сценку, которую они могут представить своим одноклассникам. Если они заинтересованы в том, чтобы найти способ запомнить шаги, они, скорее всего, быстро научатся. 6. Реле длинного деления Превратите практику длинных дивизий в веселую классную игру с эстафетами длинных дивизий. Разделите свой класс на команды и сделайте карточки с задачами на деление в длину. Объедините учащихся в группы. Каждая группа получает карточку для начала, и первые учащиеся выполняют первый набор шагов для своей проблемы. Когда они закончат, второй учащийся ищет ошибки и продолжает решать задачу. Если они решат задачу, они могут позвонить вам, чтобы проверить их работу и обменять правильный ответ на карточку с новой задачей. Продолжайте, пока каждая группа не ответит на все свои карточки, и посмотрите, какая команда победит! 7. Сундук с сокровищами Это задание — веселый способ для вашего класса отпраздновать завершение отряда в дивизионе. Возьмите несколько коробок и наполните их небольшим угощением, которое понравится всем в классе. Включите список задач на умножение, которые учащиеся должны решить в группах, чтобы «открыть» коробку. В качестве дополнительной задачи сделайте это кодом: пусть каждое частное соответствует букве алфавита, чтобы учащиеся должны были правильно расшифровать ключевую фразу, чтобы открыть коробку. 8. Генератор рабочих листов Рабочие листы — это проверенный материал на уроках математики. К счастью для вас, существует множество веб-сайтов, которые сделают всю работу за вас и сгенерируют пользовательский рабочий лист, который даст вашим ученикам возможность практиковаться в делении в большую сторону. Вот некоторые из наших любимых: Заключительные мысли по обучению учащихся делению в длинную Самое важное, что следует помнить при обучении студентов делению в столбик, это не торопиться с изучением материала. Это большая концепция, которая отличается от всего, что они изучали раньше, и некоторые (если не все) ваши ученики поначалу могут испытывать затруднения. Если вам нужно, вернитесь к более простым уравнениям и некоторым из предыдущих шагов, которые мы описали. для вас и работайте над ними, пока ваши ученики не почувствуют себя уверенно.
Это должно помочь им понять взаимосвязь между дробями и разрядным значением и может стать хорошей возможностью изучить основы дробей.
Ответ должен быть 220.
И пока они развлекаются, вы помогаете им развивать навыки длинного деления. Это победа для всех!
Напишите задачу на доске, а затем дайте учащимся черновик и возможность решить ее и посмотреть, есть ли она у них на карточках. Как всегда, побеждает тот, кто первым заполнит весь ряд!
