Содержание
Деление чисел с остатком: формулы, примеры и правила
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
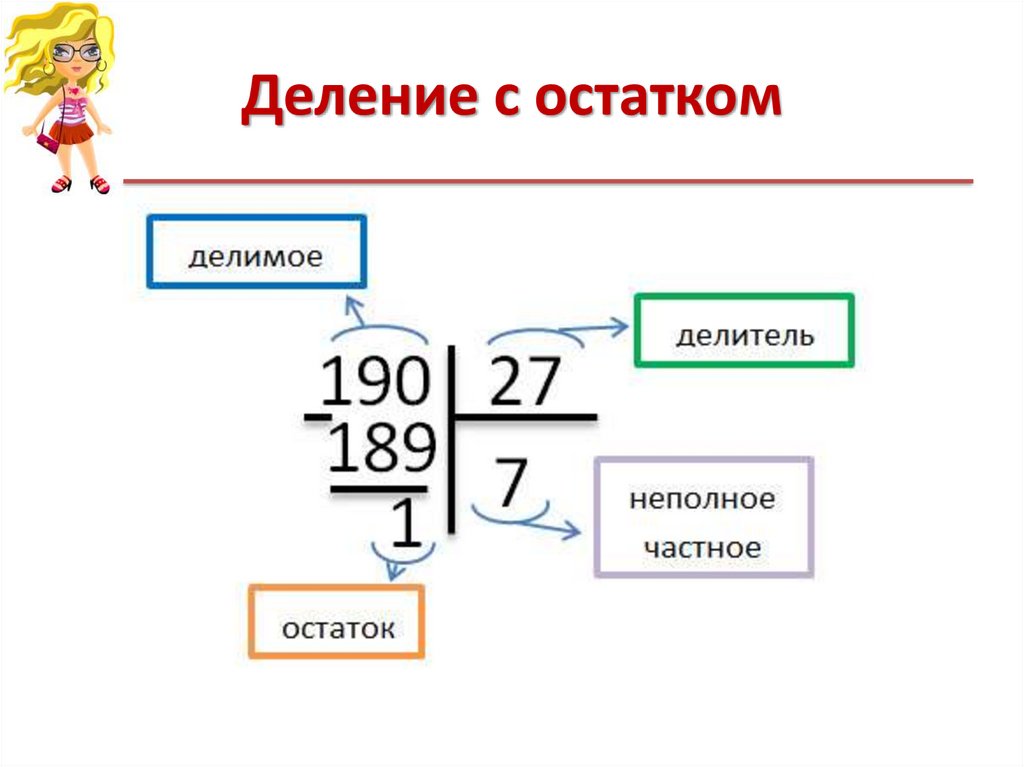
Теорема a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r < |b|. |
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил.
Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком a = b * c + d, где a — делимое, b — делитель, c — неполное частное, d — остаток. |
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.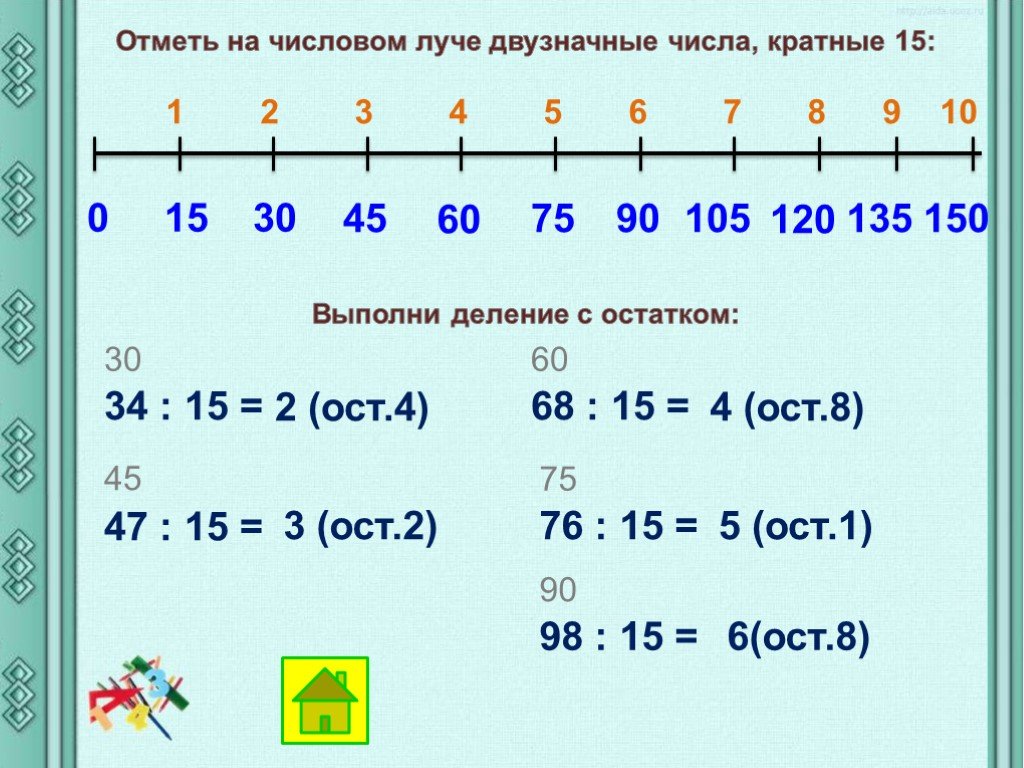
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
- 7 * 2 + 1 = 15;
- 2 * 7 + 1 = 15.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Самый удобный способ деления — это столбик.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Как решаем:
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|. |
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя
- получить неполное частное и остаток;
- записать число противоположное полученному.
Пример
Разделить 17 на −5 с остатком.
Как решаем:
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю.
Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Проверка : a = b * q + r, 17 = −5 * (−3) + 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. r = a − b * q |
Тогда остаток r будет вычисляться по формуле:Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
- найти модули делимого и делителя;
- разделить по модулю;
- записать противоположное данному число и вычесть 1;
- использовать формулу для остатка r = a − b * q.
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Как решаем:
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:
r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Проверка: a = b * q + r, −17 = 5 * (−4) + 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. r = a − b * q |
Тогда можно произвести вычисления по формуле:Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя;
- получить неполное частное и остаток;
- прибавить 1 к неполному частному;
- вычислить остаток, исходя из формулы r = a − b * q.
Пример
Найти неполное частное и остаток при делении −17 на −5.
Как решаем:
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Проверка: a = b * q + r, −17 = −5 * 4 + 3.
Ответ: (−17) : (−5) = 4 (остаток 3).
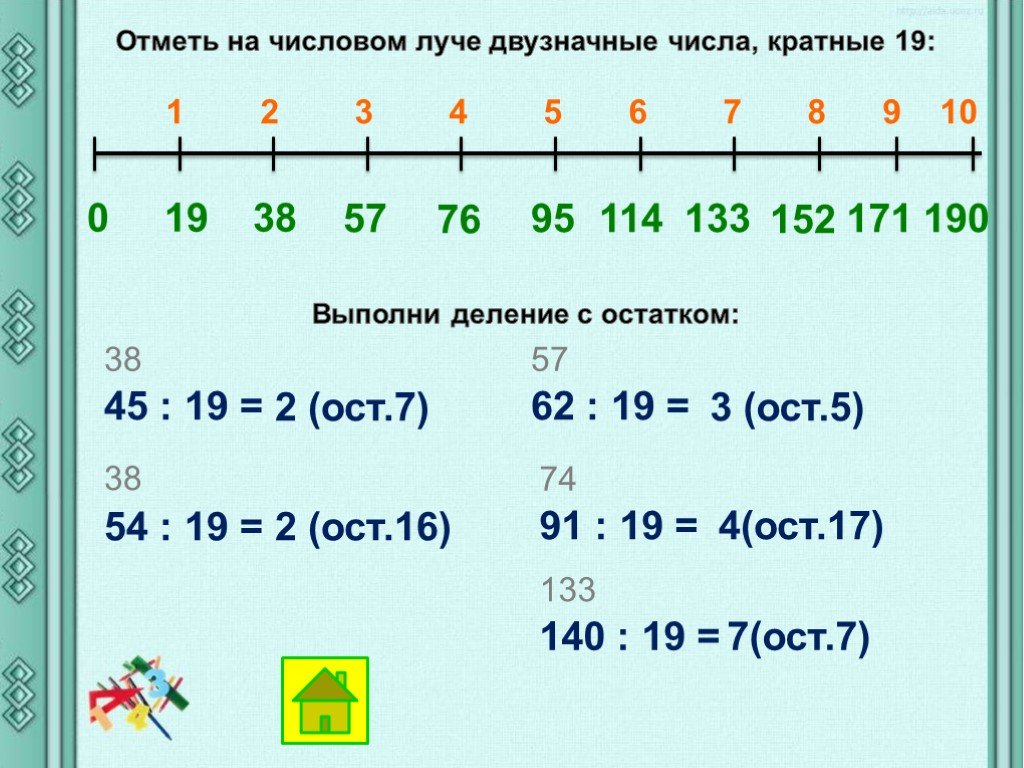
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Как объяснить ребенку деление?
Конечно же, прежде чем ваш ребенок отправится в первый класс ему необходимо освоить азы арифметики.
Первоначально ему необходимо научиться правильно, понимать задание, а так же решать его в необходимой последовательности. Лучше всего изначально научить ребенка складывать, вычитать и умножать, а уж только потом делить. Самое главное вы должны понимать, что для того чтобы ребенок понимал как выполнить то или иное действие ему необходимо все демонстрировать наглядно.
В данной статье мы подробно поговорим о том, как объяснить ребенку деление.
Как объяснить ребенку деление?
На самом деле, делить ребенок начинает еще в самом маленьком возрасте. Просто он еще до конца не осознает, что он участвует в данном процессе. Вы должны изначально объяснить ребенку, что такое целое, больше, меньше и т.д., он должен начать понимать каких игрушек больше, а каких меньше.
1. Поиграйте с малышом в деление
Для этого возьмите, к примеру, конфеты и попросите его поделиться с вами поровну. Изначально конечно ребенок будет действовать самым простым способом, он будет перекладывать конфетки по одной. В этом нет ничего страшного ведь малыш еще совсем маленький. После того как ребенок закончит делить конфеты помогите ему сосчитать сколько всего изначально их было.
Вы можете предложить малышу взять яблоки и угостить каждого члена семьи. Так же необходимо пояснить своему чаду, что не всегда, получается, разделить предметы поровну.
Приведите ему пример, что у вас есть пять подушек и вам необходимо поделить их между двумя людьми поровну. Такое попросту не возможно, потому что кому-то достанется три подушки, а кому-то две.
2. Как объяснить ребенку деление Вам подскажут обычные примеры
Объясните ребенку, что первое число это и есть те самые конфеты, а вот второе это вы и он (или еще больше участников). И главное скажите ему, что абсолютно неважно, какие именно предметы он будет делить, самое главное узнать, сколько предметов в итоге окажется у каждого из участников.
Из всего вышесказанного можно сделать вывод о том, что для того чтобы ребенок как можно быстрее понял как делить предметы, ему нужно все наглядно демонстрировать. Приводите ему как можно больше примеров, рисуйте с ним, берите какие-либо предметы и делите их. Если вы будете следовать всем перечисленным рекомендациям, то будьте уверены, ваш ребенок очень скоро сможет без труда делить числа.
Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет.
Или так: 10 монет, разложенных в стопки по 2 монеты, дадут 5 стопок.
Как выполняется деление?
Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 4 на 2 мы находим, сколько чисел 2 содержится в числе 4. Результат деления называется частным.
Как деление связано с умножением?
Деление — это операция, обратная умножению. Если вы знаете результат деления, то можете записать соответствующее произведение, и наоборот.
Возврат к исходному значению
Если 10 (делимое) поделить на 2 (делитель), то получится 5 (частное). Умножая частное (5) на делитель (2), мы получаем значение исходного
делимого (10).
Другой подход к делению
Деление также показывает, сколько раз в делимом встречаются группы, равные делителю. Ответом будет то же самое частное.
В этом примере 30 футбольных мячей делятся на группы по 3 мяча.
Получилось ровно 10 групп по 3 мяча (без остатка), поэтому 30 : 3 = 10.
Схема деления деления на однозначное число
Деление с остатком
Если одно число не делится на другое нацело, возникает остаток. Его можно преобразовать в десятичную дробь, как показано ниже.
Упрощение деления
Иногда делитель можно представить как произведение нескольких сомножителей. Тогда процедура деления сводится к нескольким более простым делениям.
Этим методом можно пользоваться и в более сложных задачах.
How to Teach Your Child Division
Детям может быть очень полезно получать помощь родителей с домашним заданием после школы, но многим взрослым трудно объяснить основные математические принципы, даже если они понимают, как их выполнять. Для родителей, которые хотят помочь своим детям с домашним заданием, следующее руководство поможет вам научить вашего ребенка делению.
Объяснение концепции деления
Прежде чем ваш ребенок сможет начать практиковаться в задачах на деление, ему сначала нужно понять концепцию деления.
Объясните им это, связав идею разделения с идеей разделения. Помогите им осмыслить это, объяснив, как некоторые элементы могут поровну распределяться между группами, и приведите им примеры. Вы можете показать им, как можно дать по шесть печений трем детям, чтобы у каждого из них было по два, или как человек с восемью яблоками может дать по четыре яблока двум друзьям.
Создавая практические примеры с наглядными ссылками, вы можете сделать так, чтобы вашим детям было легче понять концепцию деления.
Игры, которые помогут вашему ребенку понять Дивизион
Дети очень хорошо учатся визуально и кинестетически; они будут обрабатывать новую информацию быстрее, если смогут видеть ее перед собой и взаимодействовать с ней. Из-за этого может быть легче учить детей делению, создавая математические игры, чтобы расплачиваться с ними. Рассмотрите следующие игры, которые помогут вашему ребенку понять деление:
Бусины и форма для кексов
Это может быть очень сложным упражнением для детей, чтобы понять деление.
Дайте ребенку фиксированное количество бусинок и попросите его разделить их поровну между определенным количеством баночек. Начните с того, что покажите ребенку, как разделить бусины на две формочки, используя каждый раз разное количество бусин, затем постепенно переходите к делению на разные числа. Когда у ребенка останутся бусы от упражнения, у вас будет возможность объяснить ему, что осталось.
Распечатанные игры на деление
Вы можете распечатать или нарисовать головоломку на деление, где вы даете ребенку математические задачи и предлагаете ему сопоставить листы бумаги, на которых есть решение. Это хороший шаг вперед по сравнению с использованием манипулятивных действий, так как он требует, чтобы дети самостоятельно вырабатывали ответ, но все же предоставляет некоторую помощь, если она им нужна.
Обучение вашего ребенка делению в полные числа
Понимание деления в полные числа может стать еще одним трудным препятствием для детей, поскольку деление в полные числа требует более технического понимания математики, чем простое деление.
Помогите им запомнить пошаговый процесс выполнения деления в большую сторону, а затем предложите им решить задачи на деление в большую сторону. Порядок операций для деления в большую сторону следующий:
- Разделить
- Умножить
- Вычесть
- Переход к следующей цифре
При обучении детей делению на длинные числа начинайте с простых задач, которые делятся поровну, а затем постепенно вводите более сложные задачи. Используйте следующие шаги, чтобы помочь вашему ребенку освоить деление:
- Шаг 1: Основное деление, обратное вашей таблице умножения. Так как ваш ребенок имеет базовые знания об умножении и большую часть таблицы умножения знает наизусть, это хороший способ познакомить его с делением. Например, число 24 можно получить, умножив 3 и 8. Покажите ребенку, что число 24 можно разбить на 3 группы по 8 , поменяв местами факты умножения. Они также могут видеть, что 24 можно разбить на 8 групп по 3 и многие другие группы.
- Шаг 2: Введение в деление в длинную сторону без остатка. Как только ваш ребенок освоит основы деления, он может начать практиковать деление в длину. Для них будет лучше всего попрактиковаться с большими числами, которые они не могут легко вычислить в уме. Например, если ваш ребенок пытается посчитать 651, деленное на 3, ему нужно будет записать каждый шаг деления в большую сторону, чтобы получить правильный ответ. Подобные задачи помогут им попрактиковаться в шагах «умножить и вычесть».
- Шаг 3: Деление с остатком После того, как ваш ребенок усвоит этапы деления в большую сторону, пора познакомить его с остатками. Есть много приемов, позволяющих узнать, какие числа легко делятся на 2, 3, 5 и 10. Знание этих приемов поможет вам решить задачи на деление для вашего ребенка, у которого есть остатки. Объясните им, что иногда при делении остается что-то лишнее. Например, когда 3 друга хотят разделить 7 кусков пиццы, останется один кусок. Когда ваш ребенок видит, что иногда в задачах на деление остаются остатки, но может уверенно найти решение, вы помогли ему освоить деление.
Когда ваш ребенок видит, что иногда в задачах на деление остаются остатки, но может уверенно найти решение, вы помогли ему освоить деление.Деление может быть сложной концепцией для детей, когда они впервые знакомятся с ней на уроках математики. Помогите своему ребенку справиться с разделением за пределами класса, используя эти советы, чтобы он пошел в школу, вооруженный всеми знаниями, необходимыми для достижения успеха.
Ресурсы:
https://www.helpingwithmath.com/by_subject/division/div_teaching_division.htm
https://www.homeschoolmath.net/teaching/md/how_teach_long_division.php
1
Это полный урок с обучением и упражнениями по понятию остатка в делении (когда деление не точное), предназначенный для третьего класса. Он начинается с объяснения идеи остатка на примере обмена бананами.
1.
2. Разделите точки
3. Разделите и укажите остатки.
4. Потренируйтесь еще!
5. Разделить. Какие закономерности вы замечаете?
|
Сначала учащиеся работают с наглядными примерами, составляя предложения с делением с остатками. Затем урок объясняет, как найти остаток путем умножения и вычитания, чтобы найти разницу (без визуальной помощи).
14 бананов разделить на 3 человека 
Разделить на
Разделить на 
Все четыре яблока остались.
Поскольку 6 × 3 = 18 
