Как научить ребенка решать задачи по математике 4 класс задачи на: Как научить ребёнка решать задачи в 4 классе.

Содержание

«Ты просто не хочешь думать!». Почему ребёнок не может решить задачу и 5 способов ему помочь

Вечер, за окном уже темно, все собираются спать. Все, кроме школьника, который пытается решить задачу по математике. И не может. Почему? В блоге проекта «Математические тропинки» Александр Маркеллов и Екатерина Бредихина рассказывают, как помочь ребенку понимать условия задач и искать решение.

Иногда родители сталкиваются с проблемой: ребёнок сидит перед задачей и не может её решить. Что можно сделать в такой ситуации?

Сказать: «Ну ты и балбес, это же элементарно! Просто думать не хочешь!»;
Долго объяснять, потом решить самому и дать переписать;
Открыть ГДЗ и дать ребёнку списать;
Попытаться понять, в чем именно у ребёнка трудность и помочь эту трудность преодолеть.

Думаю, понятно, что плохого в первых трёх вариантах. Они могут решить проблему с вашими эмоциями или с конкретной задачей, но не помогут наладить отношения и, главное, — не научат ребёнка решать задачи самому. Скорее всего, самооценка ребёнка упадет, а в следующий раз, когда он увидит подобную задачу, у него возникнут такие же трудности.

Важное замечание: иногда нам, взрослым, то, что мы уже умеем делать, кажется элементарным, но это всего лишь иллюзия. При обучении ребёнок встречает множество трудностей, которые ему нужно преодолевать: понимать концепции, запоминать приёмы. Если вы попробуете освоить новую область, вы точно так же будете в затруднительном положении, и вам будут непонятны многие вещи. Это нормальный процесс обучения, поэтому важно признать за ребёнком право испытывать трудности.

Решение задачи — это сложный процесс, состоящий из разных этапов. В этой статье попробую показать, что это за этапы, чтобы вы могли понять, на каком из них могут возникнуть сложности у ребёнка.

Возьмем для примера такую задачу для учеников третьего класса: «Ваня, Витя и Арсений пошли собирать грибы. Всего они собрали 48 грибов. Ваня собрал на 6 грибов больше, чем Арсений. А Арсений собрал на 12 грибов меньше, чем Витя. Сколько грибов собрал каждый из ребят?».

Задачу можно решить с помощью уравнения, но в третьем классе такую задачу нужно решить по действиям. С помощью уравнения дети учатся решать задачи в пятом классе.

На мой взгляд, процесс решения задачи состоит из 5 этапов:

Прочитать условие задачи;
Понять концепцию задачи и нарисовать схему;
Решить задачу по действиям;
Записать решение;
Проверить верность решения.

В чём заключается метод? Наша задача — понять, на каком именно этапе ребёнок испытывает сложность. Мы будем помогать ребёнку с каждым этапом по очереди. Если ребёнок после этого благополучно решает задачу, значит, сложность была именно в этом этапе, и его нужно тренировать отдельно.

1. Прочитать условие

Ребёнок прочитал задачу, отлично! Но как понять, разобрался ли он, о чём там речь, или нет? Чтобы это проверить, а также помочь разобраться, что там происходит, задайте ребёнку вопросы по условию. В нашей задаче это могут быть такие вопросы:

Что надо узнать в задаче?
Сколько детей собирали грибы?
Ребята собрали одинаковое количество?
Кто собрал меньше всех?
На сколько грибов Ваня собрал больше, чем Арсений?
На сколько грибов Витя собрал больше, чем Арсений?
Что получится, если у Вани и у Вити забрать 6 и 12 грибов?
Чего не хватает, чтобы ответить на вопрос из задачи?

Если после этих вопросов ребёнок решает задачу, значит, проблема была именно на этом этапе.

Как тренировать?

Сначала давать задачи в одно действие, потом — в два действия. Просить самого задавать вопросы к задачам. Давать задачи с избыточным условием — лишней информацией, которая не нужна для решения. Это помогает фокусироваться на главном и отбрасывать ненужное. Таких задач много в учебнике «Сопрунова, Посицельская, Посицельский: Математика и информатика.»

2. Понять концепцию задачи и нарисовать схему

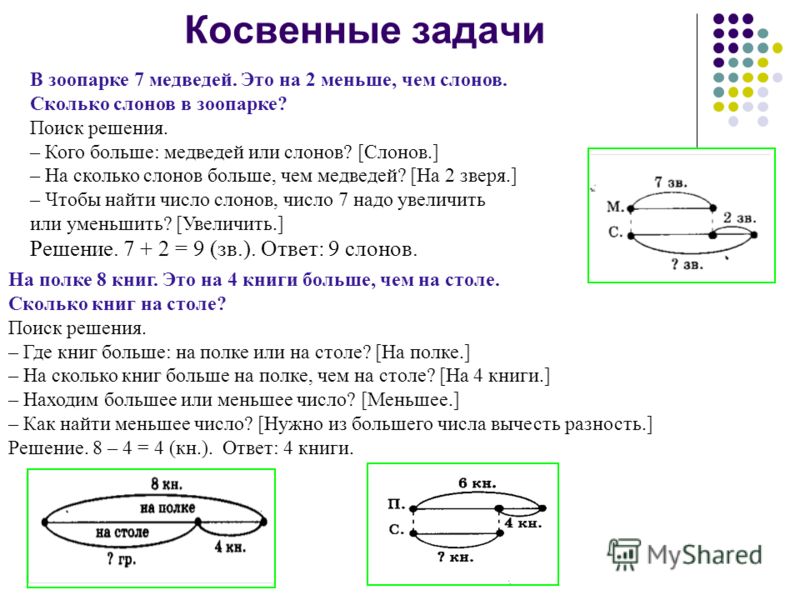
Этот этап самый сложный, так как требует понимания концепций.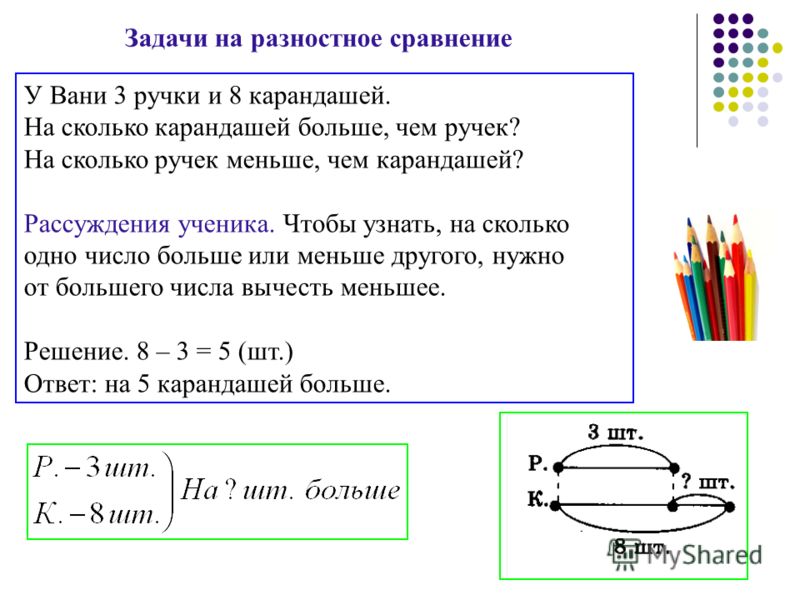 Но и его можно успешно тренировать. Если ребёнок сам не может нарисовать схему, можно предложить ему разные схемы на выбор:

Первая схема просто не соответствует условию задачи: у ребят было разное количество грибов. Вторая схема верная, но она не приближает нас к решению задачи. А вот третья схема очень точно отображает условие и позволяет с ней работать.

Как тренировать?

Уровень 1. Соедини условие и схему.

Мы столкнулись с проблемой: если у задачи есть вопрос, у ребёнка срабатывает рефлекс и он сразу бросается её решать. А нам это пока что не надо. Поэтому там, где это нам не нужно, мы убрали вопрос в задаче.

Уровень 2. Нарисуй схему к условиям.

Как ещё тренировать?

Можно делать такие задания:

Придумай задачу по схеме;
Исправь схему по описанию/исправь описание по схеме.

3. Решить по задачу по действиям

Вот как выглядит решение задачи:

У каждого типа задачи разная методология решения, которую нужно изучать, решая сначала более простые задачи. В методологию решения этой задачи мы сейчас не будем погружаться, потому что это очень узкая тема. Но остается вопрос: как тренироваться, если у ребёнка сложность на этом этапе?

Отличный способ — решать задачи именно по схеме.

4. Записать решение

Это сложный вопрос: школьная действительность такова, что почти вся проверка знаний — это письменные экзамены (контрольные, экзамены для поступления, олимпиады). Ребёнку важно уметь записывать свои мысли так, чтобы его было легко понять. Иногда в школах уделяют этому чрезмерное внимание. Важно понять, какие требования у вашего учителя и стараться их придерживаться. На мой взгляд, если ребёнок дошел до этого этапа — это здорово. Ведь он освоил навык решения задачи. Дальше уже дело техники.

5. Проверить верность решения

Важный этап, о котором не стоит забывать. Нужно посмотреть на ответ и прикинуть, похоже ли это на правду? Не получилось ли так, что пешеход у нас идет со скоростью 1000 км в час? А потом подставить ответ в условия и проверить, всё ли сходится? Хороший вопрос для ребенка, чтобы он тренировался проверять задачу: «Где обычно ошибаются другие дети?» Или «Покажи опасное место в задаче, где можно легко ошибиться». Это заостряет внимание на сложных местах в задаче.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Как научить ребенка решать типовые задачи по математике в 5 и 6 классе

математика

лайфхаки

25.04.2021

Ирина Кочковая

Педагог, преподаватель русского языка MAXIMUM EDUCATION

В этой статье:

Казалось бы, в начальной школе решают типовые задачи. Однако пятикассники часто не умеют делать это правильно. Это может стать причиной школьной неуспешности и снизить мотивацию ребенка к учебе. Важно научить ребенка решать задачи по алгоритму. Тогда он сможет самостоятельно делать домашнее задание и почувствует себя уверенно на уроках математики в школе.

Сталкивались ли вы с такой ситуацией: ваш пятиклассник битый час сидит над учебником математики и тщетно пытается что-то решить. Ваше сердце не выдерживает вид страданий маленького мученика, вы подходите и говорите: “Ну, покажи, что у тебя не получается”.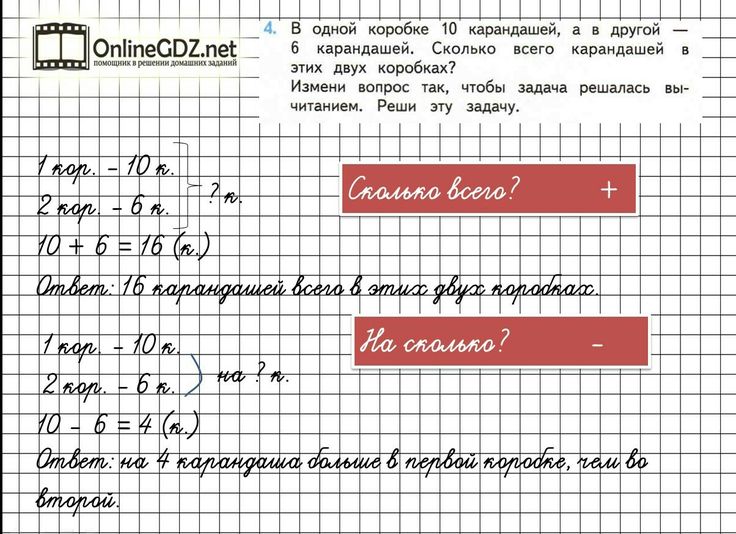 Пролистав несколько страниц тетради, вы видите: точно такая же задача была решена в классе. “Ну и что здесь сложного? Ведь ты эту задачу уже в классе решил”, — скажете вы. А ваш пятиклассник удивленно посмотрит на вас и ответит: “Как это решил? В классе мы яблоки считали, а тут орехи”.

Знакомо? Если да, ваш ребенок испытывает трудности в решении типовых задач.

Что такое типовые задачи?

Типовыми называются задачи, условия которых строятся по одному алгоритму. То есть могут меняться исходные данные, числа, но суть условия остается постоянной. Следовательно, ВСЕ задачи, относящиеся к конкретному типу, решаются по ОДНОЙ И ТОЙ ЖЕ схеме. Освоив ее, ребенок обретает универсальный “ключ” к любым задачам подобного типа.

Зачем решать типовые задачи?

Знакомясь с типовыми задачами, отрабатывая единый алгоритм их решения, ребенок учится совершать шаги, которые называют универсальными учебными действиями (УУД): умение поставить задачу, выбрать способы решения, проанализировать полученные результаты и т. д. Эти действия впоследствии ребенок будет совершать не только на уроках математики, поэтому овладение ими чрезвычайно важно. Это и есть цель решения типовых задач. Процесс овладения УУД делится на 2 этапа: 1) формирование УУД; 2) применение УУД.

Первый этап обучающиеся проходят еще в начальной школе. Именно в это время в память закладываются базовые навыки решения задач. Начиная с 5 класса ребенок учится применять эти навыки для решения конкретной задачи.

Почему у ребенка возникают проблемы при решении типовых задач?

Итак, в начальной школе уже были сформированы основные УУД и решено огромное количество типовых задач. Почему же вдруг в пятом классе ученик не всегда может справиться с, казалось бы, такими знакомыми заданиями? Причины затруднений с типовыми задачами бывают разные:

Стресс. Переход от одного классного руководителя к другому, обилие новых лиц может выбить ребенка из колеи, ввести в ступор. В результате затрудняется процесс учебной деятельности и, в частности, возникают трудности в решение задач по математике.
Высокая нагрузка. В пятом классе появляется много учебных предметов сложных, незнакомых ребенку. Учиться становится нелегко, занятия отнимают много сил. Перегруженному мозгу ничего не остается, как блокировать лишнюю информацию — например, алгоритм решения задач по математике.
Недостаточно хорошо сформированные УУД. Бывает, ребенку по той или иной причине просто не хватает базовых инструментов, чтобы решить задачу. Наша миссия в таком случае — помочь ему восполнить пробелы.
Недостаточно практики применения УУД. В начале нового учебного года пятиклассник еще не может свободно оперировать сформированными умениями. Он только учится это делать, а в процессе обучения, конечно, не обходится без ошибок и затруднений. Задача педагогов и родителей — помочь ему научиться применять имеющиеся навыки.

Как помочь ребенку решать задачи по математике в 5 классе?

Сам по себе материал не сложный. Родители могут помочь ребенку самостоятельно, если он не понял материал на уроке.

Спокойствие, только спокойствие! Ребенку непросто даются задачи — это не трагедия. Донесите эту мысль до ребенка. Этим вы убережете его от лишних волнений и избавите от парализующего страха перед заданием.
Определяем корень проблемы, чтобы понять, в какой помощи нуждается ребенок. Если трудности с математикой связаны с адаптацией к новой учебной жизни и нагрузке, то ему в большей степени нужна именно психологическая поддержка, нежели дополнительные занятия. Вечером, когда все задачи решены, поговорите с ребенком. Что ему больше всего запомнилось за день? Легко ли ориентироваться в школе? Какой предмет кажется самым интересным? Разговоры с пятиклассником о новом этапе школьной жизни помогут быстрее привыкнуть к изменениям, психологическое состояние улучшится и учиться станет легче.
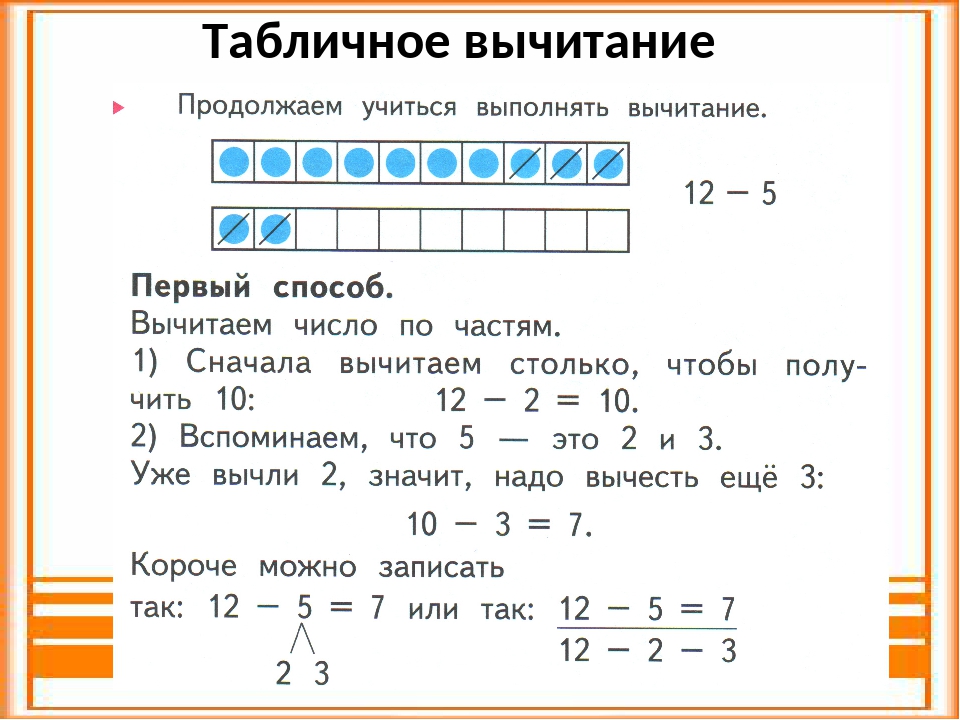
Когда же проблема именно с математикой, необходимо понять, какого рода ошибки допускает ребенок. Если, решая задачу, он использует правильный алгоритм, но путается в вычислениях, то помогут упражнения в устном счете. Только не стоит каждый день намеренно выделять время для этой цели. Пусть счет станет привычным спутником ребенка в повседневной жизни: предложите посчитать сдачу в магазине, рассчитать стоимость продуктов, отмерить количество ингредиентов при приготовлении пищи.
Если ребенок не может понять, по какому алгоритму решается задача, попробуйте ее визуализировать. Можно нарисовать условие. Например, если дана задача на движение, предложите изобразить путь, движущиеся объекты, направление перемещения. Есть и другие способы визуализации таких задач: например, возьмите линейку подлиннее — это будет дорога; игрушечные машинки — движущиеся объекты. Решайте задачу, перемещая машинки по линейке в нужном направлении. Это и внесет элемент игры, и наглядно покажет алгоритм выполнения задания.
Научите ребенка делать краткую запись задачи. Это отбросит все лишние слова и оставит суть. Это поможет быстрее отыскать необходимую формулу.
Донесите до ребенка мысль, что используемый алгоритм подходит для всех задач данного типа: попробуйте поменять в задаче числа и покажите, что формула остается неизменной. Можно также попросить его самого придумать задачу по данной формуле.
Покажите, как эти задачи могут быть применимы в повседневной жизни. Ребенку гораздо интереснее решать бытовые задачи, нежели те, которые просто записаны в учебнике.

Потренируйтесь вместе, и вам удастся преодолеть школьную неуспешность.

Принципы и алгоритмы решения типовых задач

Мало натаскать ребенка на решение задач, важно показать ему общие принципы. Благодаря им он будет справлять с аналогичными заданиями в более старших классах.

Объясняем важность задания. Расскажите ребенку, где ему пригодится решаемая задача, или предложите ему самому подумать, задавайте наводящие вопросы, мотивируйте практической пользой. Пусть ребенку захочется справиться с заданием.
Составляем краткую запись или рисуем схему.
Определяем алгоритм решения. Очень важно, чтобы ребенок сам проговорил его. Первое время можно это делать вслух, далее — про себя.
Регулярно тренируемся! Не обязательно делать это 45 минут, как в школе. Разобрав одну задачу, решите 2-3 подобных — и алгоритм прочно закрепится в памяти ребенка.

Что в итоге? Главное, не бояться говорить с ребенком и, возможно ошибаясь, искать ответ на задачи вместе. Может быть, вам, родителю, даже придется немного удивиться и поломать голову. Но это – не страшно, а даже храбро.

Почитаем ещё?

Как понять математику в школе?

12.03.2022

Преподавание математики посредством решения задач – математические методы для детей младшего возраста

Джанет Страмел

В своей книге «Как это решить» Джордж Полиа (1945) сказал: «Одна из самых важных задач учителя — помогать своим ученикам. Эта задача не совсем проста; это требует времени, практики, преданности и здравых принципов. Студент должен приобрести как можно больше опыта самостоятельной работы. Но если его оставить наедине со своей проблемой без какой-либо помощи, он может вообще не продвинуться вперед. Если учитель слишком много помогает, ученику ничего не остается. Учитель должен помогать, но не слишком много и не слишком мало, чтобы ученик получил разумную долю работы». (стр. 1)

Что такое в математике? Проблема — это «любая задача или деятельность, для которой учащиеся не имеют предписанных или заученных правил или методов, а также учащиеся не считают, что существует конкретный «правильный» метод решения» (Hiebert, et. al., 1997). Решение задач по математике — одна из самых важных тем для преподавания; обучение решению проблем помогает учащимся развить чувство решения реальных жизненных задач и применять математику к реальным ситуациям. Он также используется для более глубокого понимания математических понятий. Изучение «математических фактов» недостаточно; учащиеся также должны научиться использовать эти факты для развития своих мыслительных навыков.

Согласно NCTM (2010), термин «решение задач» относится к математическим задачам, которые потенциально могут создавать интеллектуальные задачи для улучшения математического понимания и развития учащихся. Когда вы впервые слышите «решение проблем», о чем вы думаете? Проблемы с рассказом или проблемы со словами? Сюжетные проблемы могут быть ограничены и недостаточно «проблемны». Например, вы можете попросить учащихся найти площадь прямоугольника, зная длину и ширину. Этот тип задач является упражнением в вычислениях и может быть решен бездумно, без понимания концепции площади. включает в себя задачи, которые действительно проблематичны и могут предоставить условия для математического развития учащихся.

Есть три способа решения проблем: обучение решению проблем, обучение решению проблем и обучение через решение проблем.

начинается с изучения навыка. Например, учащиеся изучают, как умножать двузначное число на однозначное, а выбранные вами сюжетные задачи — это задачи на умножение. Убедитесь, что когда вы обучаете решению задач, вы выбираете или разрабатываете задачи, которые могут способствовать развитию математического понимания.

начинается с предлагаемых стратегий решения проблемы. Например, «нарисуй картинку», «сделай таблицу» и т. д. В классах учителей можно увидеть плакаты «Метода решения задач», например: 1) Прочитать задачу, 2) Разработать план, 3) Решить. проблема, и 4) Проверьте свою работу. Существует мало или совсем нет доказательств того, что способности учащихся решать проблемы улучшаются при обучении решению проблем. Студенты будут рассматривать задачу со словами как отдельное усилие и сосредоточатся на шагах, которым нужно следовать, а не на математике. Кроме того, учащиеся будут склонны использовать метод проб и ошибок вместо того, чтобы сосредоточиться на осмыслении.

сосредотачивает внимание учащихся на идеях и осмыслении и развивает математические практики. Обучение через решение проблем также развивает уверенность учащихся и укрепляет их сильные стороны. Это позволяет сотрудничать между студентами и вовлекает студентов в их собственное обучение.

Рассмотрим следующие критерии стоящих проблем, разработанные Лаппаном и Филлипсом (1998):

Задача содержит важную и полезную математику.
Проблема требует высокого уровня мышления и решения проблем.
Задача способствует концептуальному развитию учащихся.
Проблема дает учителю возможность оценить, что изучают его ученики и где они испытывают трудности.
Учащиеся могут решать эту проблему разными способами, используя разные стратегии решения.
Проблема имеет различные решения или позволяет принимать и защищать разные решения или позиции.
Проблема побуждает студентов к участию и обсуждению.
Проблема связана с другими важными математическими идеями.
Задача способствует умелому использованию математики.
Задача дает возможность отработать важные навыки.

Конечно, не каждая проблема будет включать в себя все вышеперечисленное.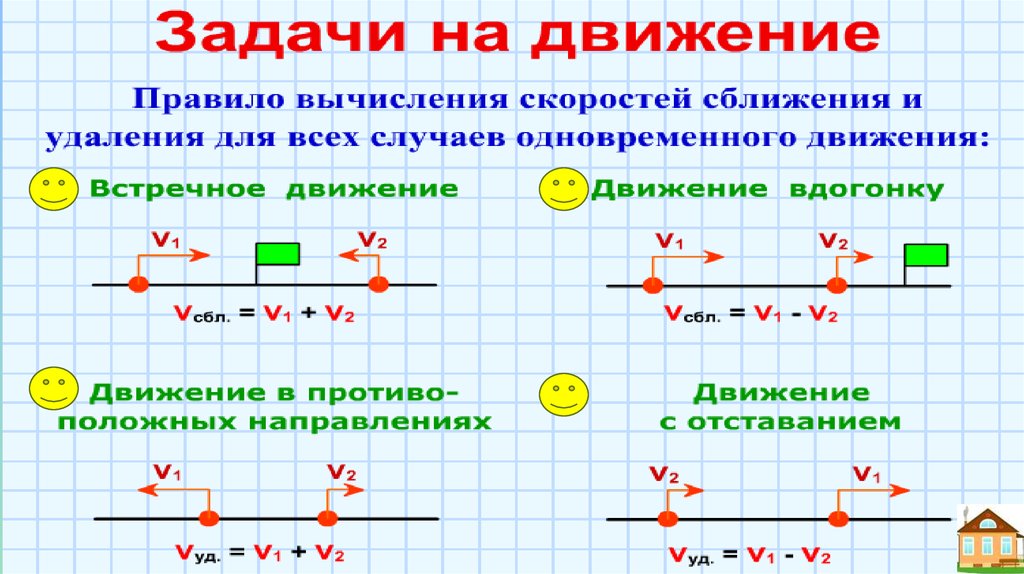 Иногда вы выбираете задачу, потому что вашим ученикам нужна возможность попрактиковаться в определенном навыке.

Ключевые особенности хорошей математической задачи включают в себя:

Он должен начинаться там, где студенты занимаются математикой.
Особенностью задачи должна быть математика, которую ученики должны изучать.
Должны требовать обоснования и пояснения как к ответам, так и к методам решения.

Решение проблем не является аккуратным и упорядоченным процессом. Подумайте о рукоделии. С лицевой стороны он аккуратный, идеальный и красивый.

Но посмотри сзади.

Он грязный и полон узлов и петель. Решение задач по математике тоже похоже на это, и мы должны помочь нашим ученикам «запутаться» в решении задач; им нужно пройти через эти узлы и петли и научиться решать проблемы под руководством учителя.

Когда вы обучаете от до решению задач , ваши ученики концентрируются на идеях и осмыслении, и они развивают уверенность в математике!

Правильный выбор задачи

Выбор видов деятельности и/или заданий является наиболее важным решением, принимаемым учителем и влияющим на обучение учащихся. Рассмотрим следующие вопросы:

Как выполняется деятельность?
Учителя должны сначала выполнить задание. Что проблематичного в деятельности? Что вам нужно будет сделать ДО мероприятия и ПОСЛЕ мероприятия? Кроме того, подумайте, как ваши ученики будут выполнять задание.
Какова цель деятельности?
Какие математические идеи будут развиваться в ходе занятия? Есть ли связь с другими темами, связанными с математикой, или другими областями контента?
Может ли данное занятие достичь цели/целей обучения?

Низкий пол, высокие потолки

По определению, «» — это математическая деятельность, которую каждый в группе может начать, а затем продолжить на своем уровне вовлеченности. Задания с низким полом и высоким потолком — это задания, которые каждый может начать и выполнять в зависимости от своего уровня, и у учащихся есть множество возможностей для решения более сложной математики. Один из показателей того, является ли действие заданием с низким полом и высоким потолком, — это когда работа над задачами становится более важной, чем сам ответ, и ведет к насыщенному математическому дискурсу [Hover: способы представления, мышления, разговора, согласия и несогласия ; как происходит обмен идеями и что они влекут за собой; и как они формируются задачами, которые учащиеся выполняют, а также характером учебной среды].

Сильные стороны использования задач с низким полом и высоким потолком:

Позволяет учащимся показать, что они могут, а не то, что не могут.
Обеспечивает дифференциацию для всех учащихся.
Способствует созданию позитивной атмосферы в классе.
Развивает у учащихся установку на рост
Соответствует стандартам математической практики

Примеры некоторых заданий с низким полом и высоким потолком можно найти на следующих сайтах:

YouCubed – под классами выберите Низкий пол Высокий потолок

NRICH Создание класса с низким порогом и высоким потолком
Математические задачи месяца изнутри

Математика в 3-х действиях

«Математика в 3-х действиях» был разработан Дэном Мейером, чтобы вызвать интерес и вовлечь учащихся в математические исследования, дающие пищу для размышлений. Математика в 3-х актах — это математическое задание для всей группы, состоящее из трех отдельных частей:

Акт первый о том, как замечать и удивляться. Учитель показывает учащимся изображение, видео или другую ситуацию, которая их привлекает и сбивает с толку. Затем учащиеся задают вопросы по ситуации.

В Act Two учитель предлагает ученикам некоторую информацию, которую они могут использовать при поиске решения проблемы.

Третий акт — «раскрытие». Учащиеся делятся своими мыслями и решениями.

«Математика в 3-х действиях» — это увлекательный способ вовлечь учащихся. Низкая точка входа придает учащимся уверенность, существует множество путей к решению, и это побуждает учащихся работать в группах над решением проблемы. Некоторые примеры Математики в 3-х действиях можно найти на следующих сайтах:

Математические задачи Дэна Мейера в трех действиях

Грэм Флетчер, 3 акта, задания]
Математика в 3-х актах: математические задачи из реального мира, чтобы сделать математику контекстной, визуальной и конкретной

Телефонные разговоры

Числовые беседы — это короткие 5-15-минутные обсуждения, посвященные решению учащимися математических задач в уме. Учащиеся вслух рассказывают о различных математических процессах в уме, а учитель визуально записывает их мысли на диаграмме или доске. Кроме того, учащиеся учатся на стратегиях друг друга, задавая вопросы, критикуя или опираясь на общие стратегии. Чтобы использовать «цифровой разговор», вы должны включить следующие шаги:

Учитель предлагает учащимся решить задачу в уме.
Укажите правильное «.»
Учитель подзывает учеников и спрашивает: «О чем вы думали?» и «Объясните свое мышление».
Для каждого учащегося, вызвавшегося поделиться своей стратегией, напишите на доске свое мнение. Обязательно точно записывайте их мысли; не исправлять свои ответы.
Предложите учащимся задавать друг другу вопросы об их стратегиях, сравнивать и сопоставлять стратегии и просить разъяснений о стратегиях, которые сбивают с толку.

«Числовые разговоры» можно использовать как введение, разминку перед уроком или как дополнение. Некоторые примеры Number Talks можно найти на следующих веб-сайтах:

Внутренние разговоры по математике
Числовые разговоры строят числовое мышление

Говорить «Это легко»

«Это просто». Три маленьких слова, которые могут оказать большое влияние на учащихся. Что может быть «легко» для одного человека, может быть «сложнее» для другого. И фраза «это легко» противоречит цели класса с мышлением роста, где учащимся удобно делать ошибки.

Когда учитель говорит «это легко», ученики могут подумать,

«Все остальные понимают, а я нет. Я не могу этого сделать!»
Учащиеся могут просто сдаться и отдать математику своим одноклассникам.
Студенты могут отключиться.

Вместо этого вы и ваши ученики можете сказать следующее:

«Думаю, я смогу это сделать».
«У меня есть идея, которую я хочу попробовать».
«Я уже встречал подобные проблемы».

Трейси Загер написала короткую статью «Это просто»: маленькая фраза, которая вызывает большие проблемы», которая может дать вам больше информации. Прочитайте статью Трейси Загер здесь.

Использование «Рабочих листов»

Вы хотите, чтобы ваши ученики запоминали понятия или чтобы они понимали и применяли математику в различных ситуациях?

Что такое «рабочий лист» по математике? Это задание на бумаге и карандаше, когда никакие другие материалы не используются. Рабочий лист не позволяет вашим учащимся использовать практические материалы/манипуляторы [Hover: физические объекты, которые используются в качестве учебных инструментов для вовлечения учащихся в практическое изучение математики]; и рабочие листы часто представляют собой «голые числа» без контекста. И рабочий лист не должен использоваться для улучшения практической деятельности.

Ученикам нужно время, чтобы исследовать материалы и работать с ними, чтобы изучить математические концепции. Рабочие листы — это всего лишь тест на механическую память. Учащимся необходимо развивать эти навыки мышления более высокого порядка, а рабочие листы не позволят им этого сделать.

Одно продуктивное убеждение из публикации NCTM «Принципы действия» (2014) гласит: «Учащиеся всех классов могут извлечь пользу из использования физических и виртуальных манипулятивных материалов для создания визуальных моделей ряда математических идей».

Вам могут понадобиться «рабочие листы», «графические органайзеры» и т. д. при планировании занятий/уроков по математике, но не забудьте включить в них практические манипуляции. Использование манипуляторов может

Предоставьте своим ученикам мост между конкретным и абстрактным
Служить моделями, поддерживающими мышление учащихся
Предоставить другое представление
Поддержка участия студентов
Предоставьте учащимся право собственности на собственное обучение.

Взято из «5 основных причин использования манипулятивных средств в классе».

Новые математические советы и стратегии для быстрого решения задач для детей

Новая математика не нова. Он был разработан в начале 1960-х годов французскими и немецкими математиками. Но это название не прижилось до недавнего времени, когда педагоги начали использовать его, чтобы помочь детям быстрее выучить математику.

Что такое новая математика и как она помогает детям?

Новая математика использует более наглядный и конкретный подход, чем традиционный способ обучения математике. Например, используя метод 10 кадров, чтобы научиться сложению и вычитанию.

10-кадр — это набор из 10 блоков с точками во всех. Если вам нужно вычесть пять, вы стираете точки в пяти ячейках, считаете, сколько точек еще осталось, и записываете ответ.

Если вы изучаете сложение и вам нужно сложить 2+5, вы поставите 2 точки в 2 клетки, а затем поставите 5 точек в 5 клеток. Затем вы считаете точки и пишете ответ.

Вот пример:

Смотрите также:

Учебная программа Common Core State Standards (CCSS) по математике также была разработана с учетом новой математики. Цель состоит в том, чтобы научить детей понимать концепции, лежащие в основе математики, а не просто запоминать шаги.

Преимущества новой математики

Обучает навыкам решения проблем и критическому мышлению.

Попытка решить проблему традиционным способом может разочаровать детей. С новой математикой им предлагается подумать о разных способах решения проблемы. Это помогает им развивать критическое мышление и навыки решения проблем, которые они могут использовать в других сферах своей жизни.

Это более наглядный и практический подход, который облегчает детям понимание концепций.

Поскольку дети используют много конкретных материалов, таких как блоки, стержни Кюизенера и манипуляторы, им становится легче визуализировать концепции и понимать, что они делают.

На основе последних исследований о том, как дети лучше всего учатся.

По мере появления новых исследований разрабатываются новые методы и материалы, помогающие детям учиться лучше. Он постоянно развивается, чтобы дети получали наилучшее образование.

Соответствует общепринятым государственным стандартам, поэтому дети узнают, что им нужно знать для стандартизированных тестов.

Новые математические стандарты Common Core были созданы, чтобы гарантировать, что все дети изучают одни и те же вещи. Обучая новой математике, дети будут подготовлены к тестам, которые они будут сдавать в школе, и не столкнутся с большим неравенством в обучении, если им придется переехать в другой школьный округ.

Гибкость и возможность адаптации к различным стили обучения .

Разные дети учатся по-разному. Некоторые учатся визуально, в то время как другие лучше всего учатся на практике. Благодаря новой математике методы обучения концепциям стали более гибкими, так что все дети могут учиться эффективно.

Помогает учащимся понять сложные понятия.

Традиционный способ обучения математике часто требует от учащихся заучивания множества шагов и формул. С новой математикой учащимся предлагается подумать о концепциях, лежащих в основе математики, чтобы они могли лучше понять ее. То, что вначале кажется маленькими шагами, к концу превращается в большое понимание.

Он готовит студентов к курсам математики более высокого уровня.

Поскольку основное внимание уделяется пониманию, а не зубрежке, учащиеся будут лучше подготовлены к курсам математики более высокого уровня, где им нужно будет уметь применять свои знания.

Это более увлекательно и весело, чем традиционные учебные программы по математике.

Посмотрим правде в глаза, математика может быть скучной. Но с новой математикой появилось больше практических занятий и игр, которые делают изучение математики более увлекательным.

   Связанное чтение:    Лучшие математические игры для детей, в которые интересно играть

Как возникла New Common Core Math?

В 2009 году при поддержке Центра передового опыта Национальной ассоциации губернаторов (NGA Center) и Совета директоров государственных школ (CCSSO) была запущена инициатива Common Core State Standards. – 12 образовательных стандартов по математике и английскому языку или грамотности (ELA) в США на основе международных моделей.

Новые общие базовые математические стандарты для классов K-8 были выпущены в 2010 году, а стандарты для старших классов – в 2011 году. На этом уровне учащиеся учатся считать до 100 и представлять числа с помощью предметов или рисунков. Они также изучают названия чисел и последовательность счетных чисел.

1 класс: В первом классе учащиеся расширяют свои знания о сложении и вычитании, чтобы решать задачи с числами до 20. Они также начинают понимать и описывать разрядное значение.

2 класс: Учащиеся второго класса расширяют свою работу со сложением и вычитанием, чтобы решать задачи с числами до 100. Они также начинают работать с умножением и делением.

3 класс: Учащиеся третьего класса продолжают развивать свое понимание умножения и деления и начинают работать с дробями.

4 класс: В четвертом классе учащиеся продолжают развивать свое понимание умножения и деления и начинают работать с дробями. Они также расширяют свое понимание разрядности до чисел до 1000.

5 класс: В пятом классе учащиеся расширяют свою работу с дробями, включая десятичные дроби и проценты. Они также начинают работать с решения уравнений.

6 класс: Учащиеся шестого класса расширяют свою работу с умножением и делением, включив в нее решение задач с большими числами. Они также начинают работать с отрицательными числами.

7 класс: В седьмом классе учащиеся расширяют свою работу с дробями, включая десятичные дроби и проценты. Они также начинают работать с решения уравнений.

8 класс: Учащиеся восьмого класса продолжают развивать свое понимание умножения и деления и начинают работать с алгеброй.

Объяснение старой и новой математики

Есть два основных подхода к решению математических задач: новый и старый, т. е. новая математика против старой математики. Старый способ состоит в том, чтобы пытаться делать все в уме, а новый способ заключается в использовании различных стратегий для решения проблем.

Старый способ заниматься математикой называется алгоритмическим мышлением, когда вы полагаетесь на запоминание последовательности шагов для решения задач. Это может работать для простых задач, но может быть очень сложно удержать все в голове, когда вы имеете дело с более сложной математикой.

Новые методы, помогающие детям быстрее решать математические задачи, обучая их критическому мышлению и подходу к ним с разных сторон. Это также помогает им глубже понимать концепции и видеть отношения между идеями. Кроме того, новый математический метод часто включает в себя технологии и использует наглядные пособия, которые могут помочь детям быстрее понять концепции.

Наконец, применение этих стратегий может помочь детям развить уверенность в своих математических способностях, что может привести к лучшей успеваемости в школе и к стандартным тестам.

Как вы можете помочь своему ребенку с новой математикой в качестве родителя или опекуна?

Вас смущают странные математические задачи из домашнего задания вашего ребенка? Если вы похожи на многих родителей, у вас могут возникнуть проблемы с тем, чтобы помочь ребенку с домашним заданием по математике, потому что оно сильно отличается от математики, которую вы изучали в школе.

Помимо упомянутых выше математических задач с 10 кадрами, вот некоторые распространенные типы математических задач, которые учащиеся 1-5 классов изучают:

Вот отличное видео о том, как складывать числа, используя числовые связи:

Вы можете решать задачи со словами, используя незамкнутую числовую строку. Вот видео, показывающее, как это можно сделать:

В следующем видео показано, как складывать двузначные числа путем их разложения.

   Связанное чтение:    Лучшие стратегии обучения

Обучение математическим навыкам учащихся начальной школы в классе

Вы можете развлечь своих учеников математикой в классной комнате:

1.

Используя реальные предметы:

Деньги, счеты, сферы или призмы очаровывают маленьких детей. Вы также можете использовать мармеладных мишек, карандаши, цвета или кубики, чтобы обучать детей понятиям чисел, сложения и вычитания.

2.

Измерение предметов:

Измерение предметов в классе и сравнение их размеров поможет детям лучше понять геометрию и понятия площади и объема.

Некоторые популярные игры с измерениями, в которые вы можете играть в классе:

Great Measure Hunt: В этой игре учитель прячет несколько предметов в классе. Каждый объект будет иметь разные измерения (вес, длина, высота и т. д.). Студенты должны найти объекты и записать их измерения в таблицу данных.
Кто больше весит: В этой игре учащиеся делятся на группы по два человека. Каждой группе дается набор предметов разного веса (например, книги, линейки и т. д.). Студенты должны угадать, какой предмет в их группе весит больше. Затем они могут использовать весы для измерения веса и посмотреть, были ли их прогнозы правильными.
Игра «Очень голодная гусеница»: Игра начинается с того, что учитель читает рассказ Эрика Карла «Очень голодная гусеница». После рассказа учащимся раздаются гусеницы (сделанные из бумаги), и они должны измерить гусениц с помощью линейки. Они также могут окрашивать свои гусеницы в зависимости от их длины.
Создание графиков: Вы можете использовать повседневные предметы, чтобы научить своих учеников построению графиков. Например, вы можете принести кучу разных фруктов и попросить учеников рассортировать их по цвету. Затем они могут создать график для отображения данных.

Немного творчества может добавить веселья на урок математики. Так что надень шапку мышления и начни!

3.

Установление связей:

Сделайте изучение математики родным для учащихся, включив его в свою повседневную жизнь. Например, вы можете задать им такие вопросы, как «Сколько денег вам нужно, чтобы купить рожок мороженого?» или «Сколько времени вам понадобится, чтобы дойти до парка?»

Вы также можете помочь им понять углы, попросив их встать в разные положения и описать угол, который образует их тело. Например: «Встань прямо. Теперь поднимите руку на уровне плеча. Вы сейчас делаете 9Угол 0 градусов».

4.

Регулярные занятия:

Вы можете помочь своим ученикам овладеть математическими навыками, включив их в повседневные занятия и занятия в классе. Например, вы можете начать день, попросив своих учеников решить задачу на доске, когда они войдут в класс.

Вы также можете предоставить им возможность практиковать новые навыки в свободное время или в центре. И не забывайте хвалить их, когда они добиваются успеха!

   Связанное чтение:    Лучшие математические игры в классе, которые заинтересуют ваших учеников на уроке математики

Как дружественный к математике язык может упростить математику для детей улучшить математические навыки тех, кто использует их регулярно. Китайский, японский, корейский и турецкий — вот некоторые примеры языков, дизайн которых удобен для математики.

Эти языки упрощают выполнение математических операций, поскольку в них используются простые и лаконичные слова для чисел, а грамматика разработана таким образом, чтобы упростить вычисления.

Например, в английском языке у нас есть отдельное слово для числа «11». Но в китайском, японском, корейском или турецком языке число «11» — это всего лишь «10 один».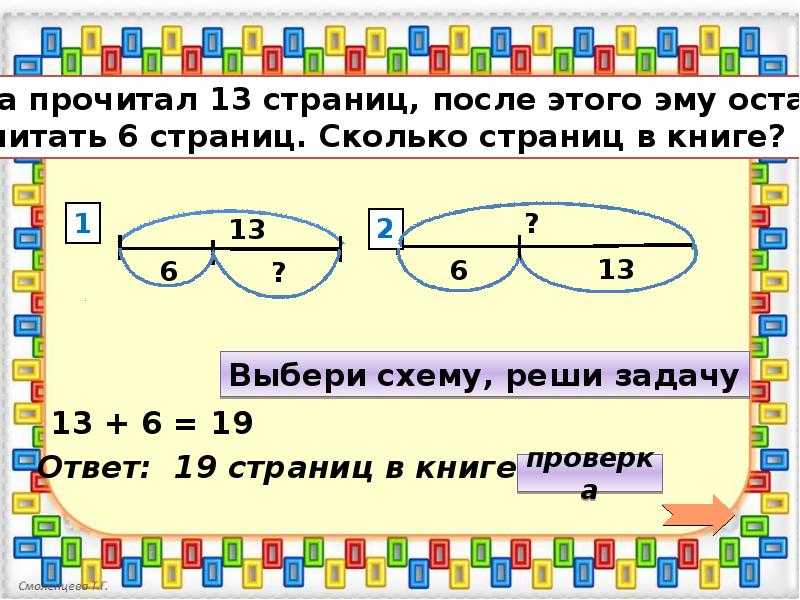 Поэтому, когда вы складываете или вычитаете числа, вам не нужно беспокоиться об отслеживании отдельного слова для «одиннадцать».

Эта конструктивная особенность дружественных к математике языков может помочь детям быстрее и легче освоить математические понятия.

Если вы говорите по-английски, вы все равно можете использовать удобные для математики языковые приемы, когда говорите со своими детьми о математике. Просто следите за тем, чтобы ваши объяснения были краткими и по существу. Например, вместо того, чтобы говорить «одиннадцать минус шесть равно пяти», вы можете просто сказать «одиннадцать, отнимите шесть, будет пять».

Вот несколько переводов стандартных математических предложений, которые облегчают задачу учащимся:

Разберитесь в этой задаче и настойчиво решайте ее — Попробуйте решить эту задачу столько раз, сколько захотите.
Используйте абстрактные и количественные рассуждения для решения этой задачи – Сначала подумайте об этой задаче без ручки и бумаги, а затем решите ее.
Используйте жизнеспособные аргументы и критикуйте рассуждения других по этой теме – Расскажите нам хороший план решения проблемы и обсудите стратегии, предложенные другими учениками.
Для решения задачи используйте математическое моделирование. – Используйте математические рисунки или объекты, чтобы понять и решить проблему.

Видите, как может измениться математический язык? Попробуйте использовать некоторые из этих фраз в следующий раз, когда будете помогать ребенку с домашним заданием по математике.

   Похожие материалы:    Как помочь детям с математикой: 6 инновационных подходов

Часто задаваемые вопросы (FAQ)

Играет ли язык роль в новой математике?

Да, язык играет роль в новой математике. Слова, которые мы используем для описания математических понятий, могут повлиять на то, насколько легко учащиеся усвоят эти понятия. Например, фразу «одиннадцать минус шесть равно пяти» труднее понять, чем «одиннадцать, отнимите шесть, будет пять». Поэтому, когда это возможно, используйте понятный для математики язык, когда говорите со своими детьми о математике.

Разве таблица умножения не была в порядке? Зачем нам их менять?

Старый способ обучения умножению (известный как таблица умножения) больше не считается самым эффективным способом обучения этому понятию. Новое исследование показало, что более концептуальное понимание умножения более полезно в долгосрочной перспективе.

При использовании старого метода ученики просто запоминали таблицы умножения и могли повторять их, не понимая, что они делают. Благодаря новому подходу учащиеся учатся визуализировать умножение и понимать лежащие в его основе концепции. Это помогает им решать более сложные задачи и применять свои знания в различных ситуациях.

Как лучше всего поощрять моего ребенка к изучению математики?

Дети лучше учатся, когда им нравится предмет.