Содержание
Как научить ребенка решать уравнения
Одна и самых сложных тем в начальной школе — решение уравнений.
Усложняется она двумя фактами:
Во-первых, дети не понимают смысл уравнения. Зачем цифру заменили буквой и что это вообще такое?
Во-вторых, объяснение, которое предлагается детям в школьной программе, непонятно в большинстве случаев даже взрослому:
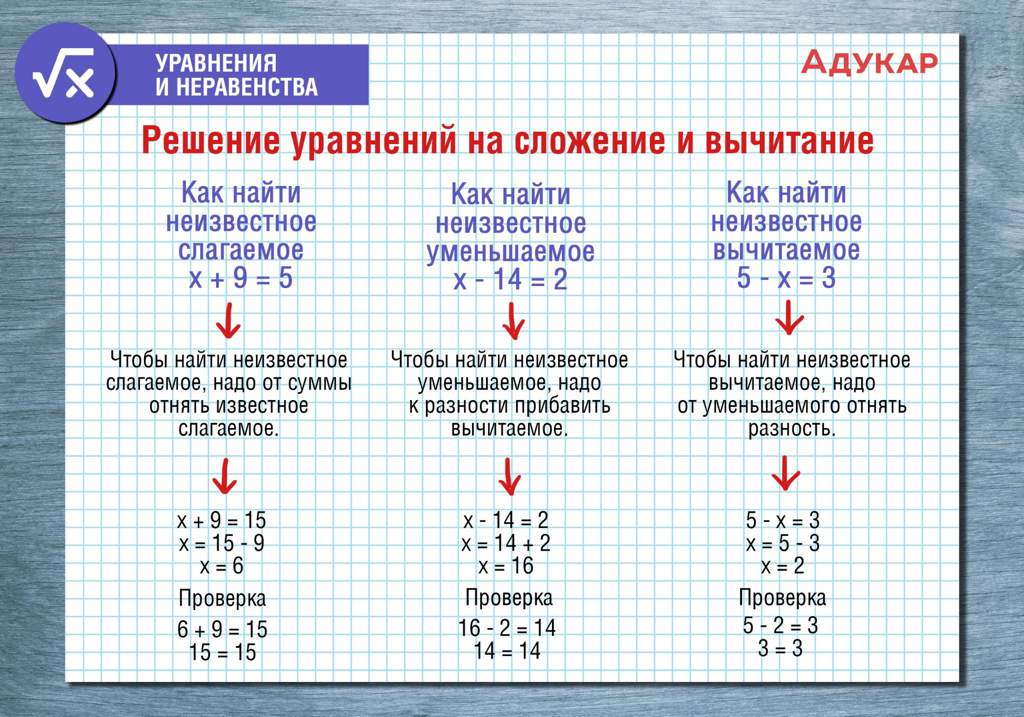
Для того чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Для того чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Для того чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
И вот, придя домой ребенок чуть ли не плачет.
На помощь приходят родители. И посмотрев в учебник, решают научить ребенка решать «проще».
Нужно же всего лишь перекинуть на одну сторону цифры, поменяв знак на противоположный, понимаешь?
Смотри, х-3=7
Минус три переносим с плюсом к семерке, считаем и получается х=10
В этом месте у детей обычно происходит сбой программы.
Знак? Поменять? Перенести? Что?
— Мама, папа! Вы ничего не понимате! Нам в школе по-другому объясняли!!!
— Тогда и решай как объясняли!
А в школе, тем временем, продолжается тренировка темы.
1. Вначале нужно определить какой компонент действия нужно найти
5+х=17 — нужно найти неизвестное слагаемое.
х-3=7 — нужно найти неизвестное уменьшаемое.
10-х=4 — нужно найти неизвестное вычитаемое.
2. Теперь нужно вспомнить правило, упомянутое выше
Для того чтобы найти неизвестное слагаемое, нужно…
Как Вы думаете, трудно ли маленькому ученику все это запомнить?
А еще нужно добавить сюда тот факт, что с каждым классом уравнения становятся все сложнее и больше.
В итоге и получается что уравнения для детей одна из самых сложных тем математики в начальной школе.
И даже если ребенок уже в четвертом классе, но у него трудности с решением уравнениями, скорее всего у него проблема с пониманием сути уравнения. И надо просто вернуться назад, к основам.
И надо просто вернуться назад, к основам.
Сделать это можно за 2 простых шага:
Шаг первый — Надо научить детей понимать уравнения.
Нам потребуется простая кружка.
Напишите пример 3 + 5 = 8
А на дне кружки «х». И, перевернув кружку, закройте цифру «5»
Что под кружкой?
Уверены, ребенок сразу угадает!
Теперь закройте цифру «5». Что под кружкой?
Так можно писать примеры на разные действия и играть. У ребенка происходи понимание, что х = это не просто непонятный знак, а «спрятанная цифра»
Подробнее о технике — в видео
Шаг второй — Научите определять, х в уравнении является целым или частью? Самым большим или «маленьким»?
Для этого нам подойдет техника «Яблоко»
Задайте ребенку вопрос, где в данном уравнении самое большое?
5+х=17
Ребенок ответит «17».
Отлично! Это будет наше яблоко!
Самое большое число — это всегда целое яблоко. Обведем в кружок.
А целое всегда состоит из частей. Давай подчеркнем части.
5 и х — части яблока.
А раз х — это часть. Она больше или меньше? х большое — или маленькое? Как его найти?
Важно отметить, что в таком случае ребенок думает, и понимает, почему, чтобы найти х в данном примере, нужно из 17 вычесть 5.
Умничка!
После того, как ребенок поймет, что ключем к правильному решению уравнений является определить, х — целое или часть, он легко будет решать уравнения.
Потому что запомнить правило, когда понимаешь его гораздо проще, чем наоборот: вызубрить и учиться применять.
Данные техники «Кружка» и «Яблоко» позволяют научить ребенка понимать, что он делает и зачем.
Когда ребенок понимает предмет, он у него начинает получаться.
Когда у ребенка получается, ему это нравится.
Когда нравится, появляется интерес, желание и мотивация.
Когда появляется мотивация — ребенок учится сам.
Учите ребенка понимать программу и тогда процесс учебы станет отнимать у Вас значительно меньше времени и сил.
Вам понравилось объяснение данной темы?
Именно так, просто и легко, мы учим родителей объяснять школьную программу в «Школе умных детей».
Хотите научиться объяснять материалы ребенку также доступно и легко, как в этой статье?
Тогда регистрируйтесь бесплатно на 40 уроков школы умных детей прямо сейчас по кнопке ниже.
Получить 40 уроков Школы умных детей бесплатно>>
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Как научиться решать простые и сложные уравнения
Как научиться решать простые и сложные уравнения
Уважаемые родители!
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для многих смежных дисциплин. В послешкольной жизни реальной необходимостью становится непрерывное образование, что требует базовой общешкольной подготовки, в том числе и математической.
В школе математика служит опорным предметом для многих смежных дисциплин. В послешкольной жизни реальной необходимостью становится непрерывное образование, что требует базовой общешкольной подготовки, в том числе и математической.
В начальной школе закладываются не только знания по основным темам, но и развивается логическое мышление, воображение и пространственные представления, а также формируется интерес к данному предмету.
Соблюдая принцип преемственности, мы сделаем упор на важнейшую тему, а именно «Взаимосвязь компонентов действий при решении составных уравнений».
С помощью данного урока можно без труда научиться решать усложненные уравнения. На уроке вы подробно познакомитесь с пошаговой инструкцией решения усложненных уравнений.
Многих, родителей ставит в тупик вопрос – как же заставить детей научиться решать простые и сложные уравнения. Если уравнения простые — это еще пол беды, но ведь бывают и сложные – например интегральные. Кстати, для сведения, есть и такие уравнения, над решением которых бьются лучшие умы нашей планеты и за решение которых выдаются очень весомые денежные премии. Например, если вспомнить Перельмана и невостребованную им денежную премию в размере нескольких миллионов.
Например, если вспомнить Перельмана и невостребованную им денежную премию в размере нескольких миллионов.
Однако вернемся для начала к простым математическим уравнениям и повторим виды уравнений и названия компонентов. Небольшая разминка:
_________________________________________________________________________
РАЗМИНКА
Найди лишнее число в каждом столбике:
2) Какого слова не хватает в каждом столбике?
3) Соедините слова из первого столбика со словами из 2 столбика.
«Уравнение» «Равенство»
4) Как вы объясните, что такое «равенство»?
5) А «уравнение»? Это равенство? Что в нем особенного?
слагаемое сумма
уменьшаемое разность
вычитаемое произведение
множитель равенство
делимое
уравнение
Вывод: Уравнение – это равенство с переменной, значение которой надо найти.
_______________________________________________________________________
Предлагаю каждой группе написать на листке фломастером уравнения: (на доску)
1 группе — с неизвестным слагаемым; 2 группе — с неизвестным уменьшаемым; 3 группе – с неизвестным вычитаемым; 4 группе – с неизвестным делителем; 5 группе – с неизвестным делимым; 6 группе – с неизвестным множителем. | 1 группа х + 8 = 15 2 группа х – 8 = 7 3 группа 48 – х = 36 4 группа 540 : х = 9 5 группа х : 15 = 9 6 группа х * 10 = 360 |
Один из группы должен на математическом языке прочитать свое уравнение и прокомментировать их решение, т. е. проговорить выполняемую операцию с известными компонентами действий (алгоритм).
Вывод: Умеем решать простые уравнения всех видов по алгоритму, читать и записывать буквенные выражения.
_____________________________________________________________________________
Предлагаю решить задачу, в которой появляется новый тип уравнений.
Х + 2кг 5кг и 3 кг | С какой величиной связан рисунок? Составьте и запишите по этому рисунку уравнение: Подберите для полученного уравнения подходящее уравнение: х + а = в а : х = в х : а = в х * а = в х – а = в а – х = в |
Вывод: Познакомились с решением уравнений, в одной из частей которых содержится числовое выражение, значение которого надо найти и получить простое уравнение.
________________________________________________________________________
Рассмотрим еще один вариант уравнения, решение которого сводится к решению цепочки простых уравнений. Вот один из введения составных уравнений.
а + в * с (х – у) : 3 2 * d + (m – n) Являются ли уравнениями записи? Почему? Как называют такие действия? Прочитайте их, называя последнее действие: | Нет. Это не уравнения, т. к. в уравнении должен быть знак «=».
Выражения а + в * с — сумма числа а и произведения чисел в и с; (х – у) : 3 — частное разности чисел х и у; 2 * d + (m – n) — сумма удвоенного числа d и разности чисел m и n. |
Предлагаю каждому записать на математическом языке предложение:
Произведение разности чисел х и 4 и числа 3 равно 15.
Запишите на математическом языке предложение: произведение разности чисел х и 4 и числа 3 равно 15 | (х – 4) * 3 = 15 |
ВЫВОД: Возникшая проблемная ситуация мотивирует постановку цели урока: научиться решать уравнения в которых неизвестный компонент является выражением. Такие уравнения являются составными уравнениями.
__________________________________________________________________________
А может нам помогут уже изученные виды уравнений? (алгоритмы)
На какое из известных уравнений похоже наше уравнение? Х * а = в
ОЧЕНЬ ВАЖНЫЙ ВОПРОС: Чем является выражение в левой части – суммой, разностью, произведением или частным?
(х – 4) * 3 = 15 (Произведением)
Почему? (т.к. последнее действие – умножение)
Вывод: Такие уравнения еще не рассматривались. Но можно решить, если на выражение х – 4 наложить карточку (у — игрек), и получится уравнение, которое легко можно решить, используя простой алгоритм нахождения неизвестного компонента.
При решении составных уравнений необходимо на каждом шаге осуществлять выбор действия на автоматизированном уровне, комментируя, называя компоненты действия.
↓
↓
↓
↓
|
(у – 5) * 4 = 28
|
Вывод: В классах с разной подготовкой эта работа может быть организована по-разному. В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.
В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.
_____________________________________________________________________________
ЗАКЛЮЧЕНИЕ:
Когда речь идёт о чём-нибудь очень простом, понятном, мы часто говорим: «Дело ясно, как дважды два — четыре!».
А ведь прежде чем додуматься до того, что дважды два — четыре, людям пришлось учиться много, много тысяч лет.
Многие правила из школьных учебников арифметики и геометрии были известны древним грекам две с лишним тысячи лет назад.
Всюду, где надо что-то считать, измерять, сравнивать, без математики не обойтись.
А чем дальше, тем больше и точнее нужно было считать. С каждым десятилетием математика становилась всё нужнее людям.
Трудно представить, как жили бы люди, если бы не умели считать, измерять, сравнивать. Этому учит математика.
Сегодня Вы окунулись в школьную жизнь, побывали в роли учеников и я предлагаю Вам, уважаемые родители, оценить свои умения по шкале.
Мои умения | Дата и оценка |
Компоненты действий. |
|
Составление уравнения с неизвестным компонентом. |
|
Чтение и запись выражений. |
|
Находить корень уравнения в простом уравнении. | |
Находить корень уравнения, в одной из частей которых содержится числовое выражение. | |
Находить корень уравнения, в которых неизвестный компонент действия является выражением. |
4 совета и рекомендации для обучения школьников решению линейных уравнений
Первоначально этот пост был опубликован в блоге Free to Discover.
Мои ученики приходят в восьмой класс с довольно сильными знаниями одно- и двухшаговых уравнений. В этом году с новой программой седьмого класса мои обычные ученики по математике приходят ко мне, никогда не решая уравнение с переменной на каждой стороне. В течение нескольких коротких недель мы рассмотрим двухшаговые уравнения, обсудим уравнения, включающие Распределительное свойство и Объединение одинаковых членов, решим множество уравнений, в каждой из которых есть переменная; в том числе с дробными коэффициентами и специальными решениями, а также изучать текстовые задачи со сценариями, смоделированными линейными уравнениями.
Решение линейных уравнений — очень важный навык для учащихся средних и старших классов. Крайне важно, чтобы учащиеся понимали
что
им нужно делать и
почему
им нужно это делать. В этом посте я хотел бы поделиться некоторыми стратегиями и ресурсами, которые я использую на уроках математики в восьмом классе.
1 – Носки и обувь: Понимание «обратного порядка действий»
Когда это возможно, я стараюсь связать то, что мы делаем в классе, с тем, что учащиеся понимают в своей жизни. На прошлой неделе я сравнил решение уравнений с надеванием носков и обуви. Утром при подготовке к рабочему дню сначала надеваются носки, затем обувь. Но в конце концов сначала снимается обувь, потом носки. То же верно и для уравнений. Рассмотрим уравнение 3x+1=-14. Когда x «подготовился» с использованием порядка операций, он был бы умножен на 3, а затем добавился бы 1. Итак, чтобы отменить операции, начните с удаления 1, а затем 3. Я использовал эту аналогию год за годом, и она доказала свою эффективность для моих студентов.
Итак, чтобы отменить операции, начните с удаления 1, а затем 3. Я использовал эту аналогию год за годом, и она доказала свою эффективность для моих студентов.
2 – Требовать красивой работы: запретить «Детские символы»
Мне нужны очень четкие доказательства балансировки уравнений – даже для одношаговых уравнений. Я хочу, чтобы учащиеся поняли, почему они могут складывать/вычитать/умножать/делить. Очень быстро мы переходим от одношагового обзора к решению уравнений с четырьмя и более шагами. Я обнаружил, что учащиеся, которые ленятся показывать свою работу в начале модуля, склонны спотыкаться, когда им нужно отслеживать гораздо больше шагов, переменных и чисел. Я также видел еще много ошибок с целыми числами и некорректных операций, когда работа сделана нечетко. Всегда есть какие-то стоны и стоны, но я знаю, что через неделю это имеет огромное значение.
Когда ученики демонстрируют свои прекрасные работы, я запрещаю использовать некоторые символы, которые они могли использовать в прошлом. Я «шучу», что мы с ними «расстаемся» и что это не последний их разрыв. Восьмиклассников шокирует то, что я предлагаю идею взаимоотношений, и это привлекает их внимание. Я не разрешаю учащимся использовать «х» для умножения при решении. Его можно спутать с общей переменной, а круглые скобки — лучший способ передать умножение. Я также не разрешаю использовать традиционный символ «разделить на». Я призываю своих учеников использовать дробную черту, чтобы показать свое деление. На прошлой неделе один студент сказал мне, что ему не нравится дробная черта, потому что тогда он не может сказать, дробь это или деление. Ах! Я привел пару основных примеров, чтобы показать, что они представляют одно и то же. Наконец, я не позволяю ученикам делить на дробь. Я требую умножения на обратное. Я помогаю учащимся заинтересоваться, демонстрируя, как это на самом деле экономит их время и работу, если они умножают непосредственно в своих организованных шагах.
Я «шучу», что мы с ними «расстаемся» и что это не последний их разрыв. Восьмиклассников шокирует то, что я предлагаю идею взаимоотношений, и это привлекает их внимание. Я не разрешаю учащимся использовать «х» для умножения при решении. Его можно спутать с общей переменной, а круглые скобки — лучший способ передать умножение. Я также не разрешаю использовать традиционный символ «разделить на». Я призываю своих учеников использовать дробную черту, чтобы показать свое деление. На прошлой неделе один студент сказал мне, что ему не нравится дробная черта, потому что тогда он не может сказать, дробь это или деление. Ах! Я привел пару основных примеров, чтобы показать, что они представляют одно и то же. Наконец, я не позволяю ученикам делить на дробь. Я требую умножения на обратное. Я помогаю учащимся заинтересоваться, демонстрируя, как это на самом деле экономит их время и работу, если они умножают непосредственно в своих организованных шагах.
3 – Использование подхода, основанного на открытиях, к особым случаям и стратегиям
Я большой поклонник сочетания обучения, основанного на открытиях, и традиционной практики. Особые случаи могут быть сложными для понимания. Я отношу «x=0» к особым случаям, потому что его часто путают с отсутствием решения. Чтобы помочь учащимся понять смысл и понять не решение, а все действительные числа, я создал рабочие листы на основе открытий, которые приводят учащихся к большим идеям. Они узнают не только о том, что нужно искать, чтобы идентифицировать особые решения, но и о том, что на самом деле означает наличие особого решения уравнения.
Особые случаи могут быть сложными для понимания. Я отношу «x=0» к особым случаям, потому что его часто путают с отсутствием решения. Чтобы помочь учащимся понять смысл и понять не решение, а все действительные числа, я создал рабочие листы на основе открытий, которые приводят учащихся к большим идеям. Они узнают не только о том, что нужно искать, чтобы идентифицировать особые решения, но и о том, что на самом деле означает наличие особого решения уравнения.
Я использую аналогичный подход при обучении студентов уравнениям, в которых используются дроби и десятичные дроби. Я создал рабочий лист на основе открытий, который показывает учащимся, как убрать дроби и десятичные дроби из уравнений. Они узнают, как выбрать множитель, на который они должны умножать в каждой части уравнения, и ясно заметят, насколько проще может быть работа с уравнением, если потратить время на очистку дробей или десятичных знаков с самого начала.
4 – Тренируйтесь весело и увлекательно
Лучший способ для учащихся освоить решение линейных уравнений — много практиковаться. Но практика не обязательно должна основываться на рабочих листах. Вот некоторые из упражнений, которые я использую, чтобы помочь студентам научиться решать уравнения:
Но практика не обязательно должна основываться на рабочих листах. Вот некоторые из упражнений, которые я использую, чтобы помочь студентам научиться решать уравнения:
Праздничная тематическая партнерская практика : В первые несколько лет моей преподавательской деятельности были каникулы, и я был так взволнован! Я хотел отметить праздник в своем классе, но так и не смог найти ничего математически осмысленного. Вот почему я решил создать свою линейку партнерских станций на праздничную тематику! Учащиеся путешествуют парами, каждый решает свою задачу. Если они правы, они будут иметь тот же ответ, что и их партнер. Отличная деятельность по самоконтролю. Забавный компонент расшифровки в конце тоже!
·
Практика на доске спереди : Мои восьмиклассники любят писать на моей доске. Я вызываю пятерых студентов на доску одновременно. У всех остальных есть бумага и карандаши, поэтому они продолжают практиковаться, даже если на них не обращают внимания. Я читаю вслух уравнение, которое все решают одновременно. Я меняю учеников, которые сидят у доски, чтобы все поднимались 2-3 раза.
Я читаю вслух уравнение, которое все решают одновременно. Я меняю учеников, которые сидят у доски, чтобы все поднимались 2-3 раза.
Практическая мини-доска : У меня есть набор мини-досок для использования на занятиях. Учащиеся решают уравнение на доске, затем, когда я даю сигнал, все они держат доски со своей работой и ответом, чтобы я мог быстро получить обратную связь об уровне понимания в классе и указать ученикам, с которыми мне следует связаться. .
Карточки с заданиями : Я люблю карточки с заданиями! Моя любимая стратегия использования карточек с заданиями заключалась в том, чтобы оставить их в мусорном ведре в передней части комнаты, а ключ к ответу был вывешен рядом. Каждый учащийся берет одну карточку, проверяет свой ответ и заменяет свою карточку новой, как только ответит правильно. Я делал это индивидуально или в парах.
Scavenger Hunt
: Я купил Scavenger hunt для своих учеников. Я спрятал «подсказки» в нашей аудитории, и мы отправились на «экскурсию». Учащимся нравилось выходить из обычной классной обстановки, работать в своем собственном темпе и нестандартным способом, а также в процессе находить ответы на загадки. Спасибо 21 -й Математические проекты века!
Я спрятал «подсказки» в нашей аудитории, и мы отправились на «экскурсию». Учащимся нравилось выходить из обычной классной обстановки, работать в своем собственном темпе и нестандартным способом, а также в процессе находить ответы на загадки. Спасибо 21 -й Математические проекты века!
***
Аманда Никс из Free to Discover живет в Нью-Гэмпшире со своим мужем, малышом и английской шоколадной лабораторией. Ей нравится работать со школьниками-математиками! После пяти лет работы учителем математики в восьмом классе она перешла на неполный рабочий день в качестве специалиста по математике в 5-8 классах. У нее настоящая страсть к обучению математике с использованием веселых интерактивных методов. Она имеет степень магистра математического образования Университета Лесли и считает, что учится на протяжении всей жизни. Она любит делиться своими идеями и стратегиями преподавания математики в блоге Free to Discover. Вы также можете связаться с ней на Pinterest, Facebook и Instagram!
Посетите ее магазин TpT
Как составить алгебраические уравнения для решения текстовых задач
Вы здесь: Главная → Статьи → Как составить уравнение для текстовых задач
У учащихся часто возникают проблемы с составлением уравнения для задачи со словами по алгебре. Для этого им нужно увидеть СВЯЗЬ между различными величинами в задаче. В этой статье объясняются некоторые из этих отношений.
Для этого им нужно увидеть СВЯЗЬ между различными величинами в задаче. В этой статье объясняются некоторые из этих отношений.
Меня спросили,
Мне нужен простой и полезный способ научить писать уравнения.
Пример: Хелен отрезает 2 дюйма волос каждый раз, когда идет в парикмахерскую. Если h равно длине волос до того, как она их подстрижет, а c равно длине волос после того, как она их подстрижет, какое уравнение вы используете, чтобы найти
длина волос Хелен после посещения парикмахерской?а) ч = 2 − в в) в = ч − 2
б) c = 2 − h d) h = c − 2Существует ли единый метод обучения учащихся написанию алгебраических уравнений? Мне нужна помощь.
Первое, что я делаю, когда пытаюсь понять, как научить чему-то , это анализирую собственное мышление. Как я думаю, решая это
проблема? Каковы шаги и мелкие детали? Именно эти детали и шаги, которые я могу выполнять автоматически, мне нужно объяснить студентам.
помочь им.
Видение величин и их отношений вместо цифр
В этой задаче, казалось бы, много информации, но на самом деле речь идет о распознавании величин и простых отношениях между ними.
их . Это, конечно, та же самая задача, что и перевод ситуации, объясненной словами, в математическое выражение с использованием символов.
Дети проявляют трудности в этом задании, когда они читают простую задачу со словами, а затем спрашивают: «Мне нужно умножить это или разделить?», просто угадывая действие, которое нужно выполнить с различными числами, указанными в задаче.
Студенты должны увидеть количества и ОТНОШЕНИЕ между ними. Им нужно выйти за пределы 5, 2, 10, 789 или любых других чисел в задаче и увидеть общие задействованные количества и то, как они связаны друг с другом. В очень простых текстовых задачах эта связь обычно включает только одну из четырех основных операций. Тогда в алгебре может быть больше величин и больше операций между ними.
Примеры задач на сложение
Пример. У Дженни 7 шариков, а у Кенни 5. Сколько у них вместе?
Ключевое слово вместе с говорит нам о том, что операция ДОБАВЛЕНИЕ, вероятно, необходима. Количества здесь: шариков Дженни , шариков Кенни и всего шариков . Отношения между тремя
шариков Дженни + шариков Кенни = всего шариков
Из этого общего соотношения между величинами легко написать уравнение для задачи, которое ее решает:
Связь: Шарики Дженни + Шарики Кенни = Всего шариков Уравнение: 7 + 5 = _____ Я написал ____ вместо общего количества шариков, так как это то, о чем просит задача (неизвестно).
Все это может показаться слишком упрощенным, но важно помочь детям увидеть лежащую в основе взаимосвязь между величинами. Рассмотрим теперь эту проблему:
Пример: У Дженни и Кенни вместе 37 шариков, а у Кенни 15. Сколько у Дженни?
Многие учителя могут попытаться объяснить это как задачу на вычитание, , но на самом фундаментальном уровне это примерно сложение! Он по-прежнему говорит о том, что у двух человек есть определенное количество шариков вместе . Соотношение между величинами такое же, как и выше, поэтому нам все еще нужно написать уравнение сложения.
Связь: Шарики Дженни + Шарики Кенни = Всего шариков Уравнение: _____ + 15 = 37 Тогда мы можем решить уравнение ____ + 15 = 37 с помощью
вычитание.Использование такого подхода в начальных классах поможет детям составлять уравнения
в задачах по алгебре позже.
Пример : Дженни, Кенни и Пенни вместе имеют 51 шарик.
У Кенни в два раза больше шариков, чем у Дженни, а у Пенни 12. Сколько у Дженни?Соотношение между величинами такое же, поэтому оно решается так же: путем написания уравнения сложения. Однако нам нужно чем-то обозначить количество шариков Дженни и Кенни. Шарики Дженни неизвестны, поэтому мы можем обозначить их с помощью переменной и . Тогда у Кенни 2 n шариков.
Связь: Шарики Дженни + Шарики Кенни + Шарики Пенни = Всего шариков Уравнение: нет + 2 нет + 12 = 51
Пример: Джейн находится на 79 странице своей книги.
В книге 254 страницы. Сколько страниц ей осталось прочитать?
На этот раз слово « все еще » указывает нам на аддитивную связь, в которой отсутствует одно из слагаемых. Вы можете сначала написать пустую строку для неизвестного, а позже заменить ее переменной.
страниц уже прочитано + страниц осталось прочитать = всего страниц + = Это уравнение, конечно, затем решается вычитанием, но лучше, если вы рассмотрите его как ситуацию сложения и напишете для него уравнение сложения.
Пример: Количество часов, оставшихся в дне, составляет одну треть от количества уже прошедших часов. Сколько часов осталось в сутках?
(Из 5 класса словесные задачи для детей)Вы видите общий принцип решения этой проблемы? В нем говорится о часах дня, когда несколько часов уже прошли, а некоторые остались.
Это, конечно, еще раз указывает на сложение: у нас есть одна часть дня, другая часть и сумма.
Единственная известная нам величина — это общее количество часов в день. Мы не знаем ни уже прошедших часов, ни оставшихся часов, поэтому изначально вы можете использовать две пустые строки в уравнении, которое показывает базовую связь между величинами:
часов уже прошло + часов осталось = всего часов = Тогда информация в первом предложении дает нам другую связь:
«Количество часов, которые остались в дне, составляло одну треть количества уже прошедших часов».
Мы не знаем, сколько часов прошло и сколько часов осталось. Итак, давайте использовать переменную p за прошедшие часы. Тогда мы можем написать выражение, включающее p для оставшихся часов, потому что «оставшиеся часы — это треть пройденных часов», или
.
Осталосьчаса = 1/3 p
Тогда запись 1/3 p вместо «оставшихся часов» в первом уравнении даст нам:
часов уже прошло + часов осталось = всего часов р + 1/3 стр = 24 Это можно решить с помощью базовой алгебры или методом «угадай и проверь».
Задачи на вычитание
Одной из ситуаций, указывающих на вычитание, является разница или сколько/намного больше . Однако наличие слова «еще» может указывать как на сложение, так и на вычитание, так что будьте осторожны.
Пример: Сегодня Тед прочитал 17 страниц, а Фред — 28.
Сколько еще страниц прочитал Фред?
Решение, конечно, 28 − 17 = 11, но недостаточно просто объявить это — дети должны также понять, что разность является результатом вычитания и сообщает ответ на , сколько еще .
Связь: страниц Фред прочитал − страниц Тед прочитал = разница Уравнение: 28
− 17
= __
Пример: У Грега на 17 шариков больше, чем у Джека. Джек имеет
15. Сколько у Грега?Здесь слово больше имеет другое значение. Этот
проблема не в разнице. Вопрос спрашивает, сколько
Грег есть – не то, что разница в количестве шариков.В нем просто говорится, что у Грега на 17 больше, чем у Джека, поэтому здесь слово больше просто указывает на сложение: у Грега столько же, сколько у Джека И на 17 больше, поэтому у Грега 15 + 17 шариков.
Пример: Масса Великой пирамиды на 557 тонн больше, чем у Пизанской башни. Каменный Хендж имеет массу 2695 тонн, что на 95 тонн меньше, чем у Пизанской башни. Когда-то существовала Великая пирамида, масса которой вдвое превышала массу Великой пирамиды. Какова была масса Великой пирамиды?
(Из 5 класса словесные задачи для детей)Каждое из первых трех предложений содержит информацию, которую можно перевести в уравнение. Вопрос не в сколько больше так что дело не в разнице. Одно дело, что больше, чем , другое означает, что вы добавляете. Одно дело, что меньше, чем , другое подразумевает вычитание. И одна вещь, удвоенная чем-то, указывает на умножение на 2.
Когда я прочитал эту задачу, я сразу увидел, что могу писать уравнения из разных предложений задачи, но не мог
смотри ответ сразу.Я полагал, что, написав уравнения, смогу продвинуться вперед; вероятно, одно уравнение решается и дает ответ на другое уравнение.
Первое предложение гласит: «Масса Великой пирамиды на 557 т больше, чем у Пизанской башни». Каковы здесь величины и отношения между ними?
масса Великой пирамиды = масса Пизанской башни + 557т Второе предложение гласит: «Стоунхендж имеет массу 2695 тонн, что на 95 тонн меньше, чем у Пизанской башни».
Здесь это дает вам отношение, подобное приведенному выше, и это
на самом деле описывает массу Стоунхенджа. Это как две отдельные части
информации: «Стоунхендж весит на 95 тонн меньше, чем башня.
Стоунхендж весит 2695 тонн». Меньше означает, что вы вычитаете. Если у вас есть
проблема решить, что из чего вычитается, вы можете думать в уме
что тяжелее: Стоунхендж или башня?
либо масса Стоунхенджа = масса башни − 95т или масса башни = масса Стоунхенджа – 95т Теперь, когда известна масса Стоунхенджа, вы можете решить это уравнение, и, зная это, вы
может решить первое уравнение, а затем перейти к массе « Великой Пирамиды «.
Если учитель сразу переходит к числовым предложениям при разгадывании слова
проблемы, то учащиеся не увидят шага, который происходит в уме перед
что. Величины и отношения между ними должны быть установлены
очистите и запишите, прежде чем возиться с фактическими числами. Нахождение
эти отношения должны быть самой важной частью словесных проблем.
Можно было бы даже опустить фактические расчеты и сосредоточиться только на поиске
количества и отношения.
Проблема длины волос Елены
Проблема. Каждый раз, когда Хелен идет в парикмахерскую, Хелен отрезает 2 дюйма волос. Если
h равно длине волос до того, как она их подстрижет, а c равно длине волос после того, как она их подстрижет, какое уравнение вы используете, чтобы найти
длина волос Хелен после посещения парикмахерской?
а. ч = 2 − с с. в = ч — 2
б. c = 2 − h d. ч = с — 2
Раствор. Пока игнорируем буквы c и h ,
Пока игнорируем буквы c и h ,
какие количества? Какой принцип или связь существует между
их? Какая из перечисленных ниже возможностей верна? Что от чего отнять?
| 1. | стрижка | — | длина волос до стрижки | = | длина волос после стрижки |
| 2. | стрижка | — | длина волос после стрижки | = | длина волос до стрижки |
| 3. | длина волос до стрижки | — | стрижка | = | длина волос после стрижки |
| 4. | длина волос после стрижки | — | стрижка | = | длина волос до стрижки |
ПРОСТО, не так ли?? В исходной задаче даны уравнения
с помощью ч и с вместо длинных фраз «длина волос до
стрижка» и «длина волос после стрижки». Вы можете
Вы можете
подставьте c , h и 2 в приведенные выше соотношения, а затем сопоставьте уравнения (1) — (4) с уравнениями (a) — (d).
Помощь учащимся в написании алгебраических уравнений
Одна идея, которая пришла на ум, состоит в том, чтобы пройти через приведенные выше и другие примеры, основываясь на типичных задачах со словами в учебниках по математике, а затем перевернуть все это и предложить учащимся выполнить такие упражнения, как:
- Напишите 3 разные сюжетные задачи, решение которых основано на отношениях
заработанные деньги – потраченные на это деньги – потраченные на это деньги = оставшиеся деньги
- Напишите 3 разные сюжетные задачи, решение которых основано на отношениях
первоначальная цена − процент скидки x первоначальная цена = цена со скидкой
- Напишите 3 разные сюжетные задачи, решение которых основано на отношениях
деньги, заработанные каждый месяц − расходы/налоги каждый месяц = деньги для использования каждый месяц И
деньги для использования каждый месяц × количество месяцев = деньги для использования в течение определенного периода времени
- Напишите 3 разные сюжетные задачи, решение которых основано на отношениях
скорость × время = расстояние И
расстояние от А до В + расстояние от В до С = расстояние от А до С
Я уверен, что вы можете придумать больше подобных упражнений.
См. также:
Почему математические задачи ТАК сложны для детей начальной школы?
Подсказка: это связано с «рецептом», которому следуют многие уроки математики.
Что можно и чего нельзя делать при обучении решению задач по математике
Общие советы о том, как можно обучать решению задач в начальной, средней и старшей школе по математике.
Как я преподаю словесные задачи Андре Тоом (PDF)
Эта статья написана русским, иммигрировавшим в США и заметившим, как учащиеся УРОВНЯ КОЛЛЕДЖА испытывают трудности даже с простейшими словесными задачками! Он описывает свои идеи о том, как заполнить пробел, образовавшийся, когда учащиеся не научились решать текстовые задачи в предыдущем обучении.
Список веб-сайтов, посвященных задачам со словами и решению задач
Используйте эти сайты, чтобы найти задачи со словами для решения. Большинство бесплатно!
Комментарии
При решении текстовых задач учащиеся должны сначала решить, какая величина представляет x, а затем должны записать все остальные величины через x.