Как научить ребенка делить столбиком 4 класс многозначные числа: Выполняем деление трёхзначного числа на двузначное число. Математика, 4 класс: уроки, тесты, задания.

Деление

Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.

Что такое деление?

Деление это действие, позволяющее что-либо разделить.

Деление состоит из трёх параметров: делимого, делителя и частного.

Делимое это то что делят;
Делитель это число, показывающее на сколько частей нужно разделить делимое.
Частное это собственно результат.

Пусть у нас имеются 4 яблока:

Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:

Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:

В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.

Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос «сколько двоек в четвёрке?» и ответить: «две двойки». Действительно, если сложить две двойки, то получится число 4

В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».

Чтобы научиться делить, нужно хорошо знать таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.

Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2

Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷ 

На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.

Деление с остатком

Остаток — это то что осталось от действия деления неразделённым.

Например, пять разделить на два будет два и один в остатке:

5 : 2 = 2 (1 в остатке)

Можно проверить это умножением:

(2 × 2) + 1 = 5

Допустим, имеются пять яблок:

Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не полýчится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:

Деление уголком

Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.

Прежде чем делить уголком, человек должен знать:

• обычное деление маленьких чисел;
• деление с остатком;
• умножение в столбик;
• вычитание в столбик.

Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается  следующим образом:

Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:

Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:

Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:

Пример 2. Найти значение выражения 8 : 3

Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.

Сначала запишем данное выражение уголком:

Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:

В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три». У нас сейчас как раз такой случай. Мы взяли по два, ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:

Далее из 8 вычитаем 6. Полученное число и будет остатком:

8 : 3 = 2 (2 в остатке)

Проверка:

(2 × 3) + 2 = 6 + 2 = 8

Деление многозначного числа на однозначное

Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.

В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.

Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.

Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то её надо разделить на делитель, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то надо разделить их  на делитель, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.

Сложно? Ни чуть, если мы разберём несколько примеров.

Пример 1. Найти значение выражения 25 : 3

25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше чем три? Да. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:

Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:

Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.

Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:

Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:

25 : 3 = 8 (1 в остатке)

Проверка:

(8 × 3) + 1 = 24 + 1 = 25

Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.

В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше чем три, поэтому деление завершено. Последний остаток мéньший делителя говорит о том, что он не содержит чисел равных делителю.

В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек.

Пример 2. Разделить 326 на 4.

Смóтрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да. Значит можно выполнять деление.

Записываем уголком данное выражение:

Теперь задаём вопрос: «сколько четвёрок в числе 32?».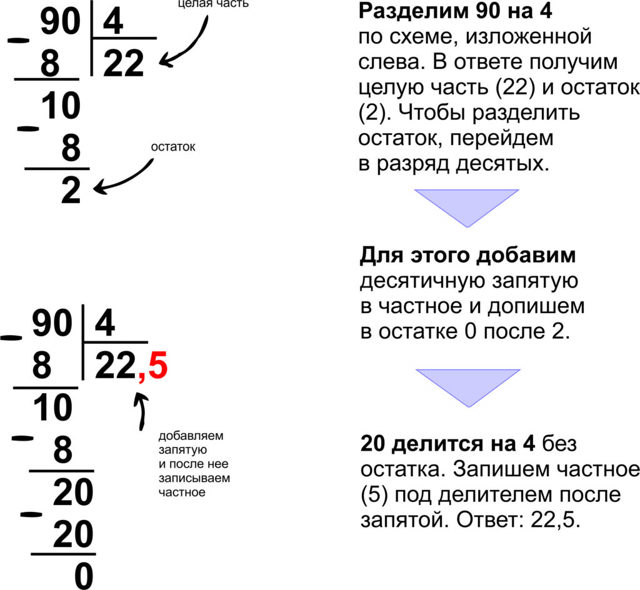 В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:

Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:

Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:

Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:

Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:

Записываем единицу в правом уголке нашего ответа:

Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:

Затем из 6 вычитаем 4, получаем число 2, которое является остатком:

Получили 326 : 4 = 81 (2 в остатке)

Проверка: (81 × 4) + 2 = 324 + 2 = 326

Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.

Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.

А в примере 25 : 3 первое неполное делимое было 25.

Пример 3. Найти значение выражения 384 : 5

Записываем данное выражение в уголком:

Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:

Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:

Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.

Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:

Умножаем 7 на 5, получаем 35 и записываем его под 38:

Теперь из 38 вычитаем 35, получим 3:

Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:

Видно, что после того, как мы снесли четвёрку, она вместе с тройкой  образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:

Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:

Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:

Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5

384 : 5 = 76 (и 4 в остатке)

Проверка:

(76 × 5) + 4 = 380 + 4 = 384

Пример 4. Найти значение выражения 8642 : 4

Этот пример немного посложнее. Записываем уголком данное выражение:

Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2

Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:

Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.

Далее сносим цифру 6 и делим её на делитель, получаем 1

Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:

Получили остаток 2. Это остаток, который остался от деления 6 на 4.

Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6

Умножаем 6 на 4, получаем 24. Записываем это число под 24

Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2

Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.

Поэтому два разделить на четыре это ноль:

Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:

Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:

8642 : 4 = 2160 (2 в остатке)

Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642

Деление чисел, у которых на конце 0

Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.

Например, разделим 120 : 3

Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:

Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.

120 : 3 = 40

Проверка 40 × 3 = 120.

Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:

12 : 3 = 4 (делимое без нулей на конце)

120 : 3 = 40 (здесь у делимого один ноль)

1200 : 3 = 400 (здесь у делимого два нуля)

12000 : 3 = 4000 (здесь у делимого три нуля)

В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.

Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5

Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:

Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.

Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.

Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:

1000 + 400 = 1400

Можно по-отдельности разделить 1000 на 5 и 400 на 5:

1000 : 5 = 200

400 : 5 = 80

и сложить полученные результаты:

200 + 80 = 280

Итого: 1400 : 5 = 280

Решим этот же пример уголком:

Деление многозначного числа на многозначное

Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так-то просто.

Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.

Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 500, 600, 1000, 13000

Любое число можно превратить в круглое. Для этого первую цифру, образующую самый старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.

Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10

Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.

Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.

Превратим число 13735 в круглое число. Первая цифра 1 образуют старший разряд (разряд десятков тысяч) — эту цифру оставляем без изменений, а остальные цифры заменяем нулями. В итоге получаем 10000.

Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут рассмотрены более подробно.

Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.

Пример 1. Найти значение выражения 88 : 12

Записываем данное выражение уголком:

Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.

Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».

Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число которое меньше делимого, но очень близко к нему или равно ему.

Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12

Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.

Пробуем следующее число. Допустим частное равно 5

Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.

Попробуем сразу взять по 8

На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7

Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.

88 : 12 = 7 (4 в остатке)

Проверка: (12 × 7) + 4 = 84 + 4 = 88

Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.

Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.

Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.

Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.

В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.

Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:

800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)

800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)

900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)

400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)

320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)

Заметно, что всё в конечном итоге свóдится к таблице умножения.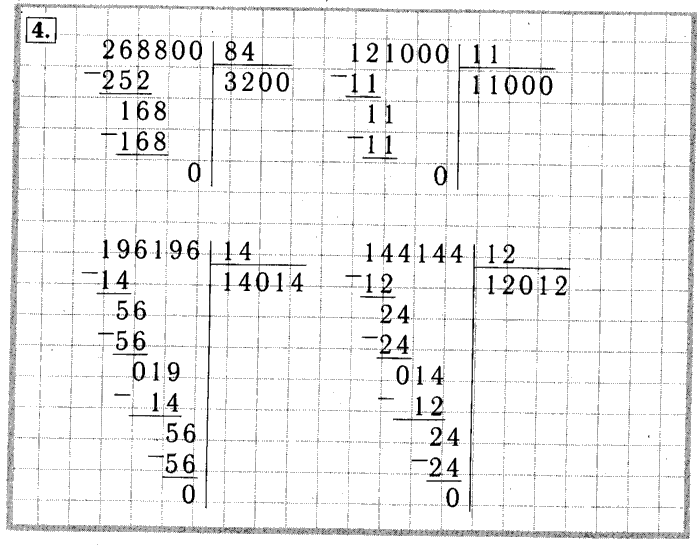 Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.

Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.

Для начала превращаем делимое и делитель в круглые числа.

Круглым числом для 88 будет число 80.

А круглым числом для 12 будет число 10.

Теперь делим полученные круглые числа:

80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:

Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.

Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.

Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:

Как видно, этим способом мы решили этот пример намного быстрее.

Пример 2. Найти значение выражения 1296 : 144

Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:

Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.

Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.

Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144

Десятка не подходит, поскольку при умножении получается число, которое больше делимого.

Попробуем взять по 9, уменьшив десятку на единицу.

Проверяем девятку. Для этого умножаем её на делитель:

Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296

1296 : 144 = 9

Проверка: 144 × 9 = 1296

Пример 3. Попробуем решить большой и сложный пример 227 492 : 331

Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.

Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300

Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:

Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:

Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.

Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:

288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:

Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:

Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:

Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:

Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.

Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241

241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:

Теперь делим 2412 на 331. Возьмём по 7

Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:

227 492 : 331 = 687 (95 в остатке)

Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492

На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.

Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.

Задания для самостоятельного решения

Задание 1. Выполните деление:

Решение:

Показать решение

Задание 2. Выполните деление:

Решение:

Показать решение

Задание 3. Выполните деление:

Решение:

Показать решение

Задание 4. Выполните деление:

Решение:

Показать решение

Задание 5. Выполните деление:

Решение:

Показать решение

Задание 6. Выполните деление:

Решение:

Показать решение

Задание 7. Выполните деление:

Решение:

Показать решение

Задание 8. Выполните деление:

Решение:

Показать решение

Задание 9. Выполните деление:

Решение:

Показать решение

Задание 10. Выполните деление:

Решение:

Показать решение

Задание 11. Выполните деление:

Решение:

Показать решение

Задание 12. Выполните деление:

Решение:

Показать решение

Задание 13. Выполните деление:

Решение:

Показать решение

Задание 14. Выполните деление:

Решение:

Показать решение

Задание 15. Выполните деление:

Решение:

Показать решение

Задание 16. Выполните деление:

Решение:

Показать решение

Задание 17. Выполните деление:

Решение:

Показать решение

Задание 18. Выполните деление:

Решение:

Показать решение

Задание 19. Выполните деление:

Решение:

Показать решение

Задание 20. Выполните деление:

Решение:

Показать решение

Задание 21. Выполните деление:

Решение:

Показать решение

Задание 22. Выполните деление:

Решение:

Показать решение

Задание 23. Выполните деление:

Решение:

Показать решение

Задание 24. Выполните деление:

Решение:

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

§ Умножение в столбик. Как умножать в столбик

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

• Геометрия: начальная школа
• Действия в столбик
• Деление с остатком
• Законы арифметики
• Периметр
• Порядок действий
• Разряды и классы. Разрядные слагаемые
• Счет в пределах 10 и 20

Математика 5 класс

• Взаимно обратные числа и дроби
• Десятичные дроби
• Натуральные числа
• Нахождение НОД и НОК
• Обыкновенные дроби
• Округление чисел
• Перевод обыкновенной дроби в десятичную
• Площадь
• Проценты
• Свойства сложения, вычитания, умножения и деления
• Среднее арифметическое
• Упрощение выражений
• Уравнения 5 класс
• Числовые и буквенные выражения

Математика 6 класс

• Масштаб
• Модуль числа
• Окружность. Площадь круга
• Отношение чисел
• Отрицательные и положительные числа
• Периодическая дробь
• Признаки делимости
• Пропорции
• Рациональные числа
• Система координат
• Целые числа

Алгебра 7 класс

• Алгебраические дроби
• Как применять формулы сокращённого умножения
• Многочлены
• Одночлены
• Системы уравнений
• Степени
• Уравнения
• Формулы сокращённого умножения
• Функция в математике

Геометрия 7 класс

• Точка, прямая и отрезок
• Что такое аксиома и теорема

Алгебра 8 класс

• Квадратичная функция. Парабола
• Квадратные неравенства
• Квадратные уравнения
• Квадратный корень
• Неравенства
• Системы неравенств
• Стандартный вид числа
• Теорема Виета

Алгебра 9 класс

• Возрастание и убывание функции
• Нули функции
• Область определения функции
• Отрицательная степень
• Среднее
  геометрическое
• Чётные и нечётные функции

Алгебра 10 класс

• Иррациональные числа

Алгебра 11 класс

• Факториал

Там где кончается терпение, начинается выносливость.
Народная мудрость

на главную

Введите тему

Русский язык

Поддержать сайт

Сложение в столбик
Вычитание в столбик
Умножение в столбик
Деление в столбик

Решим пример:

• Запишем числа столбиком (одно под другим). В верхней строчке — большее число, в нижней — меньшее.

  Самая правая цифра (знак) верхнего числа должна стоять над самой правой цифрой нижнего числа.
  Сбоку слева между числами ставим знак действия. У нас это «×» (знак умножения).

• Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записывается
  под чертой под самой правой цифрой.

  Умножаем число сверху по цифре (знаку) справа налево.

  7 · 6 = 42

  У нас получилось число большее или равное «10».

  Поэтому под черту идет только последняя
  цифра результата. Это «2».
  Количество десятков произведения (у нас «4 десятка»)
  ставим над соседом слева от «7».

• Умножаем «2» на «6».

  2 · 6 = 12

  Не забудем, что над «2» стоит
  «4». Это значит, что к результату
  умножения (произведению) надо прибавить «4».

  12 + 4 = 16

  «6» записываем под чертой и
  «1» записываем над «4».

• Умножаем «4» на «6».

  4 · 6 = 24

  К произведению добавляем «1»

  24 + 1 = 25

• Переходим к умножению числа «427» на
  «3». Умножаем по тем же правилам, что и на
  «6».

Запомните!

Результат умножения на вторую цифру необходимо записывать под второй
цифрой результата первого действия умножения.

• Полученные числа под чертой складываем по
  правилам сложения в столбик.

Теперь освоив умножение столбиком, вы сможете перемножать сколь угодно большие числа.

Сложение в столбик
Вычитание в столбик
Умножение в столбик
Деление в столбик

3 идеи для обучения многозначному умножению

Вот 3 идеи FAST для обучения многозначному умножению. Эти вмешательства просты и быстры для занятых учителей.

Борьба за многозначное умножение

Звучит знакомо?

Вы уже неделю учите двузначное умножение, а ваши ученики просто не понимают .

Вы попробовали все обычные вещи, такие как раздача учащимся таблицы умножения, тестирование на время для изучения фактов и предложение поощрений. Я уверен, что вы очень старались. И ваши ученики, вероятно, тоже очень старались.

Но они до сих пор не понимают.

Закрепите это сейчас для дальнейшего использования

Вы не одиноки. И это не твоя вина.

Многие учащиеся не готовы к многоэтапному традиционному алгоритму. Точно так же многие учащиеся не владеют основными фактами умножения.

Но с этим придется смириться.

3 идеи FAST Intervention, чтобы попробовать

Используйте эти 3 идеи FAST для обучения многозначному умножению. Они выдержали испытание временем и стоят времени и усилий.

1. Помогите учащимся содержать свою работу в чистоте.

Разборчивые, выстроенные в ряд числа так важны для успеха в математике. Учащиеся просто должны иметь разборчивый почерк и правильное выравнивание, чтобы числа оставались в столбцах.

Следующие несколько советов касаются упорядочения номеров и столбцов.

Во-первых, поощряйте учеников писать красивыми острыми карандашами, чтобы их почерк был мелким и аккуратным. Тупые карандаши размазываются, а почерк жирнеет, занимает больше места.

Еще один совет, который поможет с выравниванием, — это использование математических графических органайзеров. Они отлично подходят для выравнивания чисел и столбцов.

На изображении ниже видно, как в органайзере все аккуратно расставлено. Выровненные числа и столбцы жизненно важны, когда студенты работают и учатся. Расстояние также имеет решающее значение; эти организаторы позволяют студентам работать, не перегружая их номера.

Нажмите на изображение, чтобы узнать больше.

Вам следует попробовать использовать миллиметровую бумагу или бумагу с сеткой, если ваши ученики не нуждаются в большой поддержке или готовы продвигаться к независимости. Миллиметровая бумага помогала учащимся преуспевать в математике на протяжении десятилетий и работает до сих пор. Сетки легко сохраняют числа, столбцы и строки в чистоте и порядке.

Если у вас нет времени делать свои собственные, эти наборы подготовлены и готовы к занятиям – просто распечатайте и вперед! Идеально подходит для занятых учителей со студентами, которым требуется много практики и повторений.

Щелкните по изображению, чтобы ознакомиться с полным комплектом.

Бумага для тетрадей, перевернутая боком, позволяет учащимся сохранять аккуратность в работе. Эта стратегия дешевая и ТАК ЛЕГКАЯ!

ПРИМЕЧАНИЕ: Некоторые учащиеся могут с трудом писать свои числа настолько мелкими, чтобы они аккуратно помещались между строк.

Но так как это бесплатно, то определенно стоит попробовать!

Линованная бумага для опрятности

Если вы не уверены, какие наборы подходят для ваших учеников, попробуйте один из них — БЕСПЛАТНО! Нажмите на изображение ниже, чтобы получить БЕСПЛАТНЫЙ набор и попробовать!

Нажмите, чтобы посетить Учителя платят учителям.

НАЖМИТЕ ЗДЕСЬ, чтобы узнать больше об использовании миллиметровки и органайзеров для умножения со своими учениками!

2. Давайте поработаем над беглостью фактов умножения.

Я считаю, что для обучения владению фактами можно использовать самые разные методы, и мои любимые занятия — игры.

Представленная выше игра идеально подходит для учащихся, которые впервые изучают факты умножения или нуждаются в интенсивном изучении основных фактов умножения.

Студенты просто запускают таймер и кладут карточки с ответами поверх соответствующего факта. В верхней части тренировочного коврика факты перечислены по порядку. Нижняя половина показывает перепутанные факты.

*Игра была специально разработана для того, чтобы учащиеся могли «обманывать», глядя на верхнюю часть. Это дает уверенность, поскольку их время улучшается, и студенты вскоре учатся решать проблемы, не полагаясь на верхнюю часть.

Другие варианты игр могут быть такими же простыми, как использование карточек с настольной игрой или крестики-нолики. Я предлагаю подбирать партнеров-студентов с одинаковым уровнем беглости, чтобы избежать чувства разочарования.

Даже простые игры можно использовать для закрепления фактов.

Вы можете разрешить партнерам использовать таблицу умножения для проверки ответов друг друга.

Некоторым учащимся хорошо подходят онлайн-игры и обучающие программы. Xtramath.org — надежная и полезная программа, которую я использую уже много лет. Прочтите этот пост в блоге: Xtramath.org — отличная БЕСПЛАТНАЯ программа для занятий по математике!

Использование тестов на время по-прежнему является популярным способом обучения и мотивации учащихся к изучению фактов. Если вы ищете базовый набор тестов на время умножения, ознакомьтесь с этим универсальным набором.

Даже если вы не хотите ограничивать студентов по времени, это все равно отличная практика.

3 различных формата викторин

Я также приобрел и использовал этот ресурс у другого автора, работающего над платой учителям, созданного г-ном Хьюзом. Моим ученикам понравилось это задание, и они создали свой собственный додекаэдр, к тому же они довольно круто смотрятся в классе.

От Создано г-ном Хьюзом в Учителя платят учителям

3. Предоставьте рекомендации — большие и маленькие.

Когда учащиеся решают задачи на многозначное умножение, им часто нужны напоминания и визуальные подсказки, поскольку для их решения требуется очень много шагов.

Опорные диаграммы и плакаты служат в качестве наглядных материалов и справочных материалов, которые помогают учащимся самостоятельно ответить на многие вопросы.

Нажмите на изображение, чтобы перейти на страницу «Учителя платят учителям».

Справочные плакаты и опорные диаграммы (такие как приведенный выше) могут научить учащихся полагаться на себя при решении задач и ответах на вопросы. Это способствует независимости и уверенности. Кроме того, у учителя есть больше времени, чтобы поддержать отстающих учеников, а не отвечать на одни и те же вопросы снова и снова.

Я часто использую это для проверки двузначного умножения

Я использую эту якорную таблицу двузначного умножения (выше) для частого просмотра двухзначного умножения на двузначное. Он следует тем же визуальным подсказкам, что и организаторы умножения. Он идеально подходит для учителей, которым нужно знать, как преподавать многозначное умножение.

И это многоразовый !

Обратите внимание на стикеры. Меняйте их на разные числа каждый день для частой практики! Вы можете сделать задачи настолько простыми или сложными, насколько это необходимо вашему классу.

Используйте такие плакаты и якорные диаграммы ежедневно или еженедельно для начинающих, учащихся специальных учебных заведений или всех учащихся, которым полезно регулярно просматривать их.

Краткое руководство по обучению умножению

Несколько слов напоследок. . .

При обучении многозначному умножению то, что работает для одних учащихся, может не работать для других. Оставайтесь открытыми и гибкими, пробуя новые идеи и стратегии. Многим учащимся требуется повторение и несколько раз просмотр понятий, представленных различными способами, прежде чем они найдут отклик.

Другие статьи о многозначном умножении:

Рабочие листы по двузначному умножению: дифференцированное . Вот визуальный метод обучения двузначному умножению с использованием дифференцированных визуальных подсказок, помогающих ученикам добиться успеха.

Двузначное умножение стало проще! – Вот как использовать организаторы двузначного умножения и рабочие листы.

Статьи о длинном делении:

Дифференцированные рабочие листы длинного деления БЕСПЛАТНО – Получите БЕСПЛАТНО эти дифференцированные рабочие листы с делением на длинное деление и значительно повысьте успеваемость учащихся и свои успехи в обучении!

Как преподавать многозначное умножение и деление в длинное число  – Эта статья в блоге познакомит вас с имеющимися у меня ресурсами по дифференцированному умножению и делению в длинное число. Затем вы узнаете, как именно я использую их в своем классе.

Вмешательство в математику с миллиметровой бумагой . В этой статье блога объясняется, как использовать миллиметровую бумагу в качестве быстрого и простого ресурса для вмешательства с вашими учениками. Он включает ссылки на бесплатную печатную миллиметровую бумагу и идеи по ее использованию в классе.

Пожалуйста, следите за мной в моем Магазине учителей для учителей , Pinterest и Facebook , если вы нашли эту статью полезной! Я хотел бы услышать от вас!

Эффективные стратегии обучения многозначному умножению

Многозначное умножение — сложная концепция для обучения. Давно прошли те времена, когда мы обучали одному методу, такому как длинное умножение, и просто *надеялись*, что все наши ученики поймут и смогут эффективно использовать этот метод. Сегодня мы знаем, как важно обучать многозначному умножению более стратегически. Это гарантирует, что каждый ученик в вашем классе сможет добиться успеха в той или иной степени. Это также гарантирует, что знания учащихся построены на стратегической основе и что они действительно ПОНИМАЮТ процесс многозначного умножения.

В качестве альтернативы, если вы ищете ресурс, где вся работа выполняется за вас, вас может заинтересовать эта Станция многозначного умножения, где учащиеся работают с различными стратегиями в своем собственном темпе, осваивая каждую из них по мере они идут. Стратегии интегрированы стратегическим образом, гарантируя, что учащиеся постепенно наращивают свое понимание. См. Станцию ​​многозначного умножения ЗДЕСЬ.

Итак, с чего начать обучение многозначному умножению?

Важно начать со стратегий, которые помогут учащимся решать многозначные уравнения в уме. Вместо того, чтобы сразу переходить к длинному умножению или эффективной альтернативе, начните со следующего:

1.  Коммутативные и ассоциативные свойства . В первую очередь важно, чтобы учащиеся запомнили эти свойства. Свойство коммутативности утверждает, что порядок множителей не меняет произведения. Например, 4 × 3 и 3 × 4 равны 12. Ассоциативное свойство утверждает, что факторы могут быть сгруппированы по-разному. Например, (7×2)x5 дает тот же результат, что и (2×5)x7. Эти свойства помогают учащимся понять, что они могут манипулировать уравнениями, чтобы упростить их решение.

2.  Использование коэффициентов. Это отличный способ научить учащихся тому, что числами можно манипулировать, чтобы упростить решение уравнения. Когда мы учим многозначному умножению, наша цель не всегда состоит в том, чтобы как можно быстрее получить правильный ответ. Иногда наша цель состоит в том, чтобы уметь мыслить творчески, когда дело доходит до чисел. Это один из таких случаев. Мы могли бы взять уравнение 4×15 и разбить 15 на его множители, 3 и 5. Теперь у нас есть это уравнение: 4×3×5. Теперь мы можем решить это так: (4×3)x5 -> 12×5 -> 60. Это просто для того, чтобы показать, что существует не только один правильный способ решения этого уравнения.

3.  Умножение на 10, 100 и 1000, а также умножение на 10, 100 и 1000. аккуратно, по частям. Когда вы обучаете этой концепции, важно сосредоточиться на правилах разрядности, прежде чем обучать таким приемам, как прием «добавление нулей». Например, когда учащиеся сталкиваются с уравнением 45×100, они должны понимать, что разрядные значения увеличиваются на 2 разряда, чтобы получилось 4500. Точно так же при умножении уравнения типа 3×1000 разрядные значения увеличиваются на 3. мест, чтобы получить 3000. После того, как учащиеся усвоили эту концепцию, мы можем научить их тому, что когда в множителях есть 2 нуля, мы добавляем 2 нуля к произведению. Имейте в виду, что этим трюкам следует обучать только ПОСЛЕ того, как ученики отлично разбираются в математике, лежащей в основе концепции.

4.  Разделение чисел. Это одна из самых полезных математических стратегий в уме. Он включает в себя разбиение одного из факторов, умножение на группы, а затем сложение этих групп вместе. Вот пример: в этом примере мы разбиваем 12 на 10 и 2, а затем умножаем на части. Таким образом, 12×30 становится (10×30) + (2×30). Это гораздо проще решить!

Мы также можем использовать эту стратегию для умножения больших чисел, например 103×9. Мы можем разбить 103 на 100 и 3, а затем умножить по частям, например так: (100×9) + (3×9).

5.   Метод окна/окна. Мне нравится метод «ящик/окно», потому что он использует расширенную форму каждого фактора, что делает его отличной стратегией для закрепления концепций восприятия чисел. Чтобы использовать эту стратегию, мы рисуем прямоугольник (количество столбцов и строк зависит от количества цифр в факторах), а затем записываем развернутые формы факторов сверху и сбоку. Затем мы умножаем каждую часть и складываем части вместе, когда закончим. Если вам нужно более подробное руководство по этой стратегии, см. ЭТО сообщение в блоге, которое также включает видеоурок.

6. Частичные продукты. Это одна из самых важных стратегий обучения в качестве альтернативы длинному умножению. В частичных произведениях уравнение настроено так же, как и в традиционном длинном умножении, но способ умножения отличается. Например, для уравнения 35×3 мы сначала умножаем 3×5, чтобы получить 15. Затем мы умножаем 3×30, чтобы получить 90. Обратите внимание, что мы умножаем на ТРИДЦАТЬ, а не на три. Это потому, что 3 представляет 30. Это дает нам 90. Теперь мы складываем 15 и 9.0 вместе, чтобы получить 105. Если вам нужен более подробный учебник по этой стратегии, см. ЭТО сообщение в блоге, которое также включает видеоурок.

Стратегии, которые я изложил выше, являются НАИБОЛЕЕ важными для обучения многозначному умножению. Все эти стратегии делают упор на понимание чисел и гарантируют, что учащиеся действительно понимают, что означают числа в каждом уравнении. Но как насчет таких стратегий, как традиционное длинное умножение?

Это спорная тема. Некоторые учителя считают, что наше обучение должно быть сосредоточено ТОЛЬКО на чувстве числа, поэтому мы не обучаем стратегиям, которые не фокусируются на понимании числа. Эти учителя, как правило, используют такие стратегии, как частичные произведения, в течение всего года как очень эффективную альтернативу традиционному длинному умножению. Другие учителя считают, что мы должны учить так, как много лет назад учили умножению. Тогда это работало, так почему бы не работать сейчас?! Эти учителя, как правило, больше сосредотачиваются на стратегиях, таких как традиционное длинное умножение, и меньше на более современных методах, таких как ящик/окно или частичные произведения.

Я здесь не для того, чтобы говорить вам, какой способ лучше 🙂 Это зависит от вас и ваших учеников. Тем не менее, я скажу вам свое личное убеждение. Лично я склонен не впадать ни в одну крайность. Я большой сторонник стратегий, которые способствуют пониманию числа. Однако я также считаю, что для НЕКОТОРЫХ ваших учеников есть место традиционным методам. Вам придется быть судьей здесь. Если у вас есть ученики, которые борются с многозначным умножением, вы, вероятно, решите, чтобы они сосредоточились на частичных произведениях и коробках/окнах, и остановитесь на этом. Зачем добавлять еще больше путаницы? Они могут быть очень успешными с этими стратегиями. ОДНАКО, у вас могут быть ученики, которые отлично понимают то, чему вы учили до сих пор, и готовы к более сложной задаче! Эти учащиеся могут преуспеть в других, менее ориентированных на числа методах, поскольку они уже хорошо разбираются в математических концепциях. Для этих студентов я собираюсь рассказать о нескольких других стратегиях.

Следующие стратегии в меньшей степени ориентированы на числовое восприятие, но они могут стать интересным способом умножения для тех учащихся, которые готовы к испытаниям.

1. Решеточное умножение. Это действительно забавный метод, который включает в себя рисование сетки и использование этой сетки для организации чисел. Некоторые учителя считают, что учащимся, использующим этот метод, легче переносить числа, потому что числа расположены диагональными рядами, поэтому легче увидеть, где их нужно добавить. Объяснение этой стратегии требует некоторого времени, поэтому, пожалуйста, просмотрите ЭТУ запись в блоге, которая также включает видеоурок по стратегии.